ポジショントラッキングの数学 #3D

この記事ではHTC Viveでも使われているLighthouseというポジショントラッキング技術について、数式を交えつつ解説します。¹

ポジショントラッキングとは

3次元空間上において、ヘッドマウントディスプレイ(HMD)などのデバイスやパーツなどの位置や向きを検出する仕組みです。特にVRの分野で活用されることが多く、HTC ViveやOculus RiftなどのHMDでVR空間の中を動き回れたり、コントローラを持ってVR空間に配置されたモノを掴めたりするのは、ポジショントラッキングによってVR空間で自分やコントローラの位置や向きを計算できているからです。

今回紹介するのはポジショントラッキングの中でもOutside-inトラッキングとして分類される、Lighthouseというテクノロジーです。Outside-inのトラッキングとは、外部にトラッキングのための特別なセンサーなどを設置し、HMD側では、そのセンサーが感知した情報を元にポジションを計算するものです。他によく採用されるポジショントラッキングの仕組みとしては、Inside-outの方法があり、これはHMDに埋め込まれたカメラに映る映像を元に、現在のポジションを計算するもので、Outside-inのように外部の機器を必要としません。

Lighthouseの概要

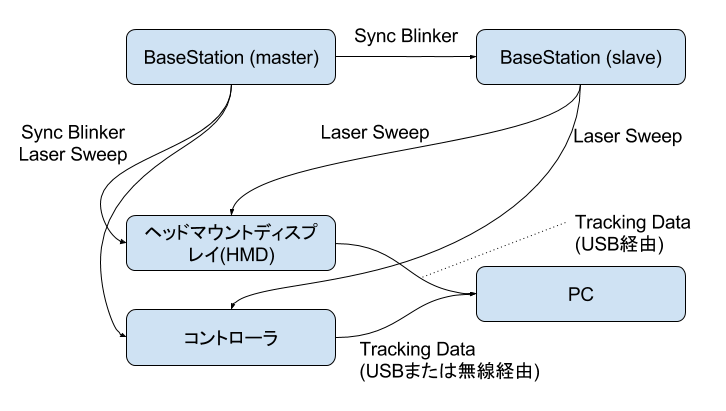
HTC ViveにおけるLigthouseのポジショントラッキングは、2台のBase Staitonと呼ばれる外部機器、トラッキング対象となるHMDとコントローラ、およびそれらのデバイスからトラッキングデータを受け取るPCによって構成されます。実際の構成図と、論理構成図を以下に載せます。

ざっくりと言うと、Lighthouseでは、2台のBase Stationが赤外レーザーを発光し、HMDなどのデバイス側で受光、その受光タイミングから、3D空間内のポジションを計算する仕組みになります。

BaseStationの発光

Base Stationから発せられる赤外光は実際には肉眼では見えませんが、発光している様子を可視化している動画があるので、引用します。

この赤外光は実際は2種類あります。LEDによる「Sync Blinker（同期点滅）」と、レーザー光による「Laser Sweep」です。Sync Blinkerは2台のBase Stationから発せられるもので、Base StationとHMD、およびコントローラ間で、これからLaser Sweepを始めるよ、というタイミングの同期のために使われる短い点滅光です。

Laser Sweepは指向性のあるレーザー光で行われる空間のスキャニングで、各BaseStationから、水平な平面で上下にSweepするレーザーと、垂直な平面で左右にSweepするレーザーの2種類のレーザー光を発します。Laser Sweepは、master/slaveそれぞれのBase Stationが行うのと、水平平面/垂直平面それぞれで行うものとで、計2x2=4パターンあります。

下図は、前出の動画からのキャプチャですが、左奥にあるBaseStationが、垂直平面で左右のSweepを行っている様子を可視化したものです。

HMD・コントローラ側で受信した赤外光がSync Blinkによるものか、Laser Sweepによるものか、また、今どのBase StationがLaser Sweepを行っているか、水平方向・垂直方向どちらのSweepなのかという情報は、赤外光の波長によって識別できます。²また、Laser Sweepは一定の速度でSweepされるので、Sync Blinkerを受光したタイミングとLaser Sweepを受光したタイミングの差によって、Base Stationから見た時のLaser Sweep平面の角度を求めることができます。

平面を計算

具体的な例を見てみましょう。以下のような座標系で、y軸と直行する水平レーザー平面が、x軸を中心に回転するケースを考えます。

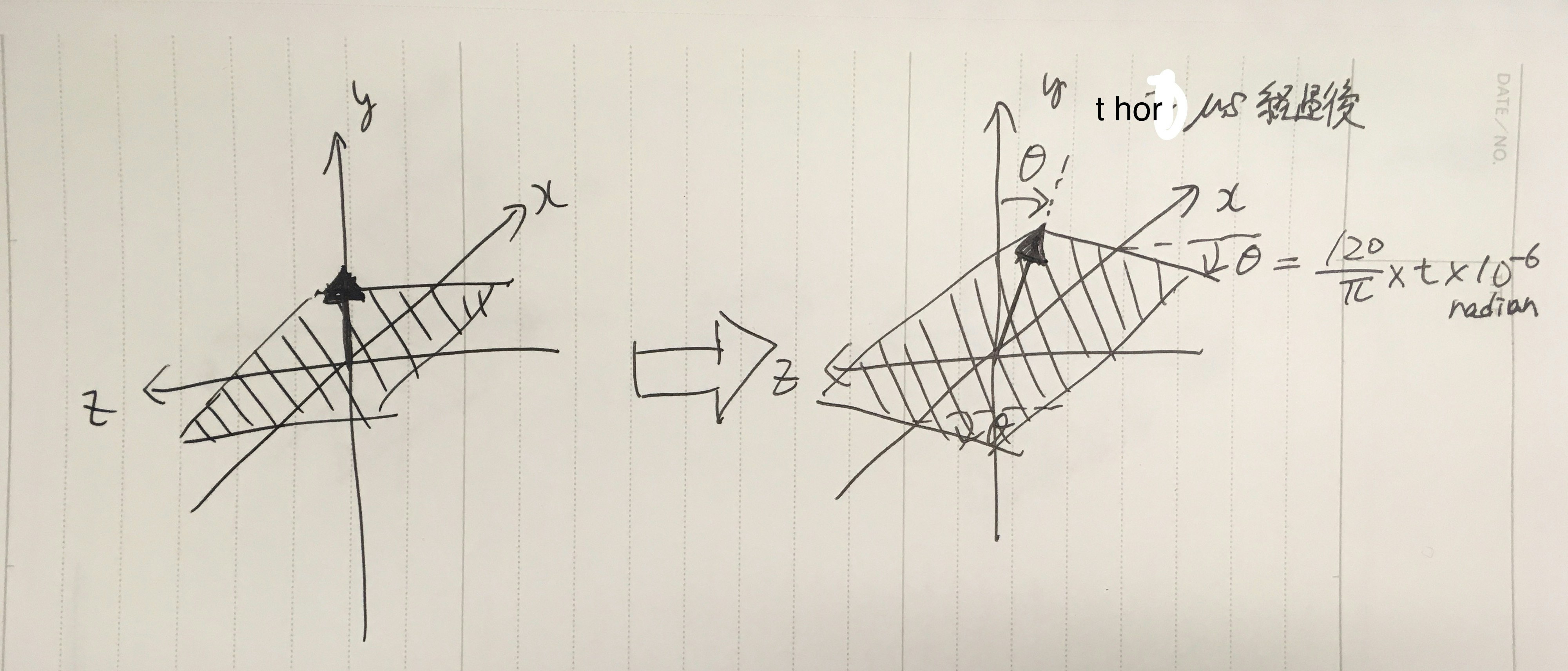
今、BaseStationでSync Blinkerが発生してから、$ t_{hor} μs $後に水平平面のLaserを受光したとします。BaseStationのレーザーの角速度は実際には $ 120\pi rad/s $ なので、水平平面の初期位置とのなす角θは、 $ \theta = 120\pi * t * 10^(-6) rad $ で求めることできます。

このとき最初の水平平面の法線ベクトルは(0, 1, 0)でしたが、t秒後の法線ベクトルは $ V_{hor} = (0, \cos \theta, \sin \theta) $ で得られます。

同様にして、z軸と直行する垂直レーザー平面が、y軸を中心に回転するケースを考えます。

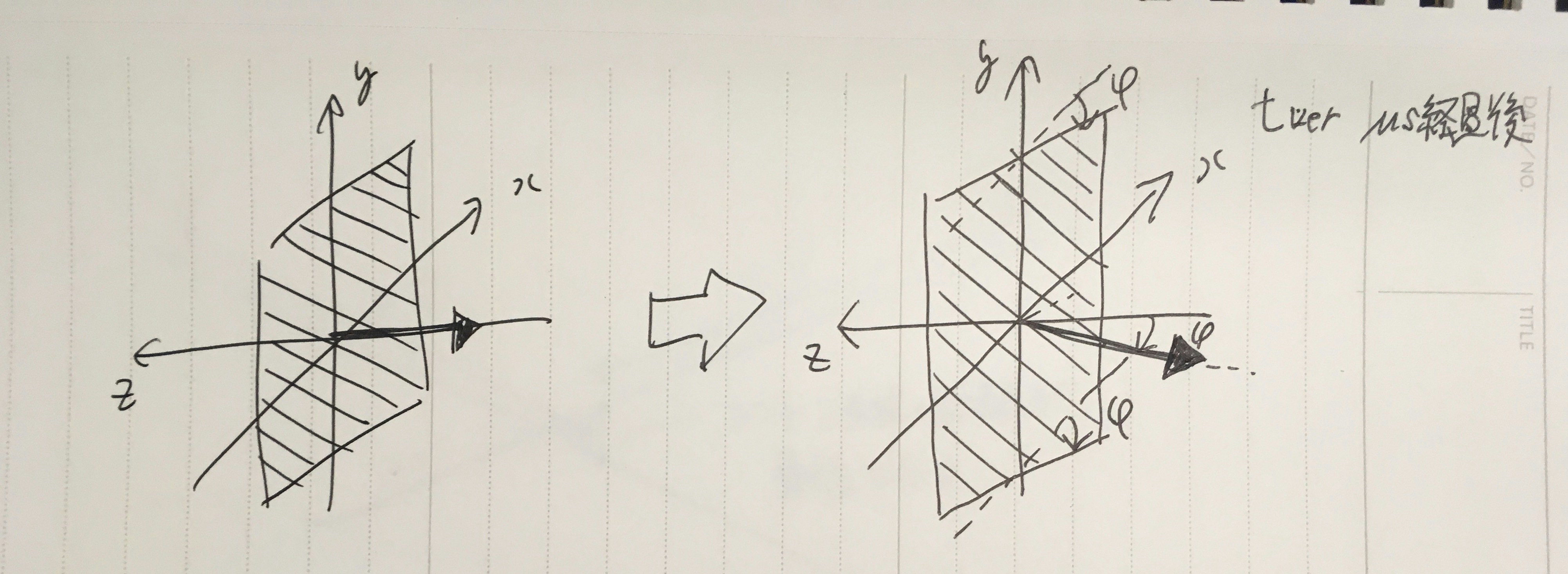
$ t_{ver} μs$後に垂直平面のレーザーの受光した場合、初期位置とのなす角をφとすると、その時の垂直レーザー平面の法線ベクトルは、$ V_{ver} = (cos(phi), 0, -sin(phi)) $ で得られることが分かります。

Base Stationから見た時の対象物体への方向ベクトルを計算

今までの計算で、BaseStationから見た時に $ V_{hor} $ と $ V_{ver} $ の2つの平面の上に、対象物体が乗っていることが分かりました。この2つの平面が交差する直線を求めることによって、BaseStationから見た時の対象物体の方向ベクトルを求められます。平面が交差する直線は、それぞれれの平面の法線ベクトルに対して直行するので、外積をとって $ V_{hor} × V_{ver} $ で求められます。BaseStationの位置から、このベクトルの向きに伸びる直線上に、対象物体は存在することになります。

2台のBase Stationの方向ベクトルの交点を計算

各Base Stationごとに対象物体への直線を求めたら、それらの直線の交点が、求める対象物体の位置になります。実際には計算された方向ベクトルには誤差が乗っているので、こららの直線が交わるケースは少ないです。そのため実際には近似値として、距離が最短となる各直線状の点を求め、その中点を対象物体の位置とします。

前段で求めた、各BaseStationからの方向ベクトルをそれぞれU・V、始点となるBaseStationの位置をそれぞれP・Qとおき、直線間距離が最短になるために s・t を変数として、$ P(s) = P+sU $ と $ Q(t) = Q+tV $ の間距離が最短になるようなs・tを求めます。距離が最短となるとき P(s)とQ(t)を結ぶ直線は、U・V両方に直交するので、
$ U・(P(s) - Q(t)) = 0 $
$ V・(P(s) - Q(t)) = 0 $
が成り立ちます。これはsとｔの簡単な連立二元方程式なので容易に解くことができて、求めるべき点の座標が得られます。

参考URL

nairol/LighthouseRedox: Lighthouse Reverse-Engineered Documentation: https://github.com/nairol/LighthouseRedox
ashtuchkin/vive-diy-position-sensor: Code & schematics for position tracking - sensor using HTC Vive's Lighthouse system and a Teensy board.: https://github.com/ashtuchkin/vive-diy-position-sensor

と書いたものの、後でほとんど数式が出ていないことに気づいた。 ↩
より詳しく知りたい方は https://github.com/nairol/LighthouseRedox/blob/master/docs/Light%20Emissions.md を参照してください。 ↩