クーポンコレクター問題：どうぶつの森で73種類の化石コンプリートには何日かかる？

はじめに

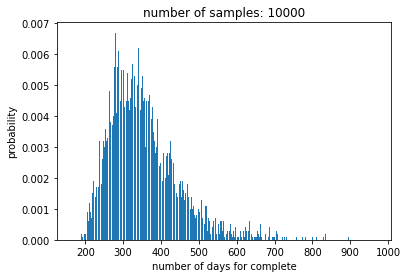
どうぶつの森の化石を1日1つ採取するとき、73種類をコンプリートする日数の分布は次のようになる。この分布から、コンプリートには約300日かかることが分かる。

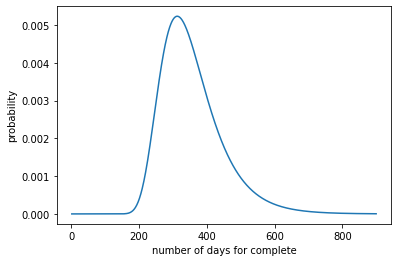
この分布を計算機的・数学的に求める。

計算機的な方法

import numpy as np
import collections
import matplotlib.pyplot as plt
import random


# randomモジュールの関数randint(a, b)はa <= n <= bのランダムな整数intを返す。
# 73個全ての化石の所有数が1以上になったときにwhileループを抜け、それまでにかかった日数を返す関数
def get_days(k):
    fossil_list = [0] * k
    days = 0
    while min(fossil_list) == 0:
        num_fossil_per_day = 1
        for i in range(num_fossil_per_day):
            fossil_list[random.randint(0, k - 1)] += 1
        days += 1

    # print(sorted(fossil_list))
    return days

# かかった日数をnum回取得して分布を取得する。numが大きいほど分布は正確になる
def days_plot(k=73, num=10000):
    days = [get_days(k) for i in range(num)]

    c = collections.Counter(days)
    key = list(c.keys())
    value = list(c.values())

    # print("最短でコンプリートできる日数:", min(key))
    left = np.array(key)
    height = np.array(value) / sampling_num
    plt.title('number of samples: {}'.format(num))
    plt.xlabel('number of days for complete')
    plt.ylabel('probability')
    plt.bar(left, height)
    plt.show()


# どうぶつの森の化石73種類
k = 73
# データサンプル数
sampling_num = 10000

# 横軸が日数、縦軸が N日目に初めて73種類の化石をコンプリートする確率分布
days_plot(k, sampling_num)

数学的な方法

from sympy.functions.combinatorial.numbers import stirling
import matplotlib.pyplot as plt
import math

# 第二種スターリング数を活用
# 詳しくは以下のwebサイトへ
# http://peng225.hatenablog.com/entry/2019/03/15/085054
k = 73
numTrial = 900
x = []
y = []
for n in range(1, numTrial+1):
    stir = stirling(n-1, k-1, kind = 2)
    prob = math.factorial(k) * stir / (k**n)
    x.append(n)
    y.append(prob)

plt.xlabel('number of days for complete')
plt.ylabel('probability')
plt.plot(x, y, label='k = {}'.format(k))

おわりに

分布をみると、1日1個化石が採れると仮定して、73種類をコンプリートするのに、200日目から300日目にかけて急峻に確率が上がり、そこからはなだらかに下がっていた。
ここから、73個の化石をコンプリートするには1年近くかかること、そして数％の人は600日以上もかかってしまうことが分かった。