はじめに
実家の親父に久々に会ったらスマホアプリで数独を解いていたので。
Google Colaboratory でやっていきます。
挑戦する問題は？
「sudoku」でググるとこういうサイトがあるようなので、ここの問題を解くことを目標にします。
「Difficulty」を見ると以下の4レベルがあるようですね。
- Easy
- Medium
- Hard
- Expert
それぞれ1問ずつ解いてみます。
実装
問題
例えば以下の問題なら、、、
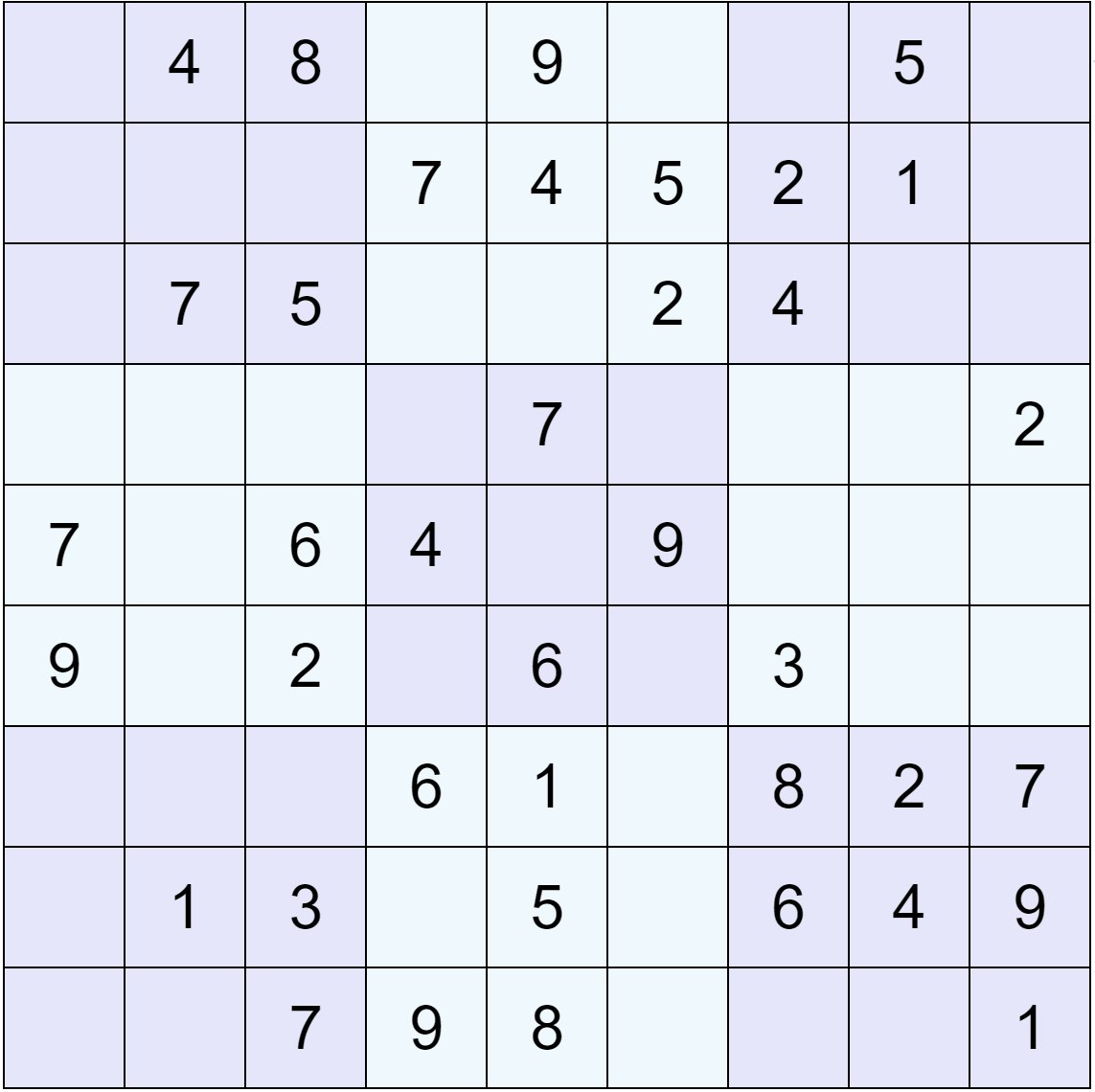
以下のように2次元リストで表現することにします。
ちなみにこの問題は難易度が easy の例ですね。
sudoku.ipynb
# easy
list_sudoku = [
[0, 4, 8, 0, 9, 0, 0, 5, 0],
[0, 0, 0, 7, 4, 5, 2, 1, 0],
[0, 7, 5, 0, 0, 2, 4, 0, 0],
[0, 0, 0, 0, 7, 0, 0, 0, 2],
[7, 0, 6, 4, 0, 9, 0, 0, 0],
[9, 0, 2, 0, 6, 0, 3, 0, 0],
[0, 0, 0, 6, 1, 0, 8, 2, 7],
[0, 1, 3, 0, 5, 0, 6, 4, 9],
[0, 0, 7, 9, 8, 0, 0, 0, 1]]
候補を絞る関数
例えば上記の問題の1番左上のセルなら、縦・横・ブロック内に既に入っている数字は入らないことが決まっているので、候補を [1,2,3,6] に絞ることができるわけですね。
これをやれる関数を作ります。
先に 1～9 の候補のリストを変数にしておきましょう。
sudoku.ipynb
list_possible = [i for i in range(1, 10)]
では関数を作ります。
まずは縦。
sudoku.ipynb
def narrow_ver(x, list_possible, list_sudoku):
"""
縦方向の候補を絞る
"""
list_ver = [list_sudoku[i][x] for i in range(9) if type(list_sudoku[i][x]) is int]
return set(list_possible) - set(list_ver)
続いて横。
sudoku.ipynb
def narrow_hor(y, list_possible, list_sudoku):
"""
横方向の候補を絞る
"""
list_hor = [list_sudoku[y][i] for i in range(9) if type(list_sudoku[y][i]) is int]
return set(list_possible) - set(list_hor)
そしてブロック内。
sudoku.ipynb
def narrow_blo(x, y, list_possible, list_sudoku):
"""
ブロック内の候補を絞る
"""
index_x = (x // 3) * 3
index_y = (y // 3) * 3
list_blo = [list_sudoku[i][j] for i in range(index_y, index_y+3) for j in range(index_x, index_x+3) if type(list_sudoku[i][j]) is int]
return set(list_possible) - set(list_blo)
縦・横・ブロック内を呼び出す関数を作って・・・
sudoku.ipynb
def narrow(x, y, list_possible, list_sudoku):
"""
対象セルの候補を絞る
"""
list_possible = narrow_ver(x, list_possible, list_sudoku)
list_possible = narrow_hor(y, list_possible, list_sudoku)
list_possible = narrow_blo(x, y, list_possible, list_sudoku)
return sorted(list(list_possible))
↑をすべてのセルに対して実行する関数を作ります。
ただし、既に数字が決まっているセルはスルーです。
sudoku.ipynb
def apply_narrow(list_sudoku):
"""
すべてのセルに対して narrow() を実行する
"""
for y in range(9):
for x in range(9):
if list_sudoku[y][x] != 0 and type(list_sudoku[y][x]) is int:
continue
elif list_sudoku[y][x] == 0:
list_sudoku[y][x] = narrow(x, y, list_possible, list_sudoku)
else:
list_sudoku[y][x] = narrow(x, y, list_sudoku[y][x], list_sudoku)
if len(list_sudoku[y][x]) == 1:
list_sudoku[y][x] = list_sudoku[y][x][0]
return list_sudoku
もしかしたらこれだけで解けるんじゃないでしょうか？
ちょっと試してみましょう！
Easy を解いてみる
temp_sudoku にコピーしておいて、apply_narrow()実行後のものと比較して、変化がなければ終了ということにします。
sudoku.ipynb
import copy
list_possible = [i for i in range(1, 10)]
count = 0
temp_sudoku = []
while(True):
temp_sudoku = copy.deepcopy(list_sudoku)
count += 1
list_sudoku = apply_narrow(list_sudoku)
if temp_sudoku == list_sudoku:
break
print(count)
list_sudoku
↓出力結果
6
[[2, 4, 8, 1, 9, 6, 7, 5, 3],
[3, 6, 9, 7, 4, 5, 2, 1, 8],
[1, 7, 5, 8, 3, 2, 4, 9, 6],
[4, 5, 1, 3, 7, 8, 9, 6, 2],
[7, 3, 6, 4, 2, 9, 1, 8, 5],
[9, 8, 2, 5, 6, 1, 3, 7, 4],
[5, 9, 4, 6, 1, 3, 8, 2, 7],
[8, 1, 3, 2, 5, 7, 6, 4, 9],
[6, 2, 7, 9, 8, 4, 5, 3, 1]]
解けましたね！やったぜ！
Medium はどうでしょう？
sudoku.ipynb
# medium
list_sudoku = [
[9, 0, 0, 8, 1, 0, 0, 0, 0],
[0, 0, 5, 0, 0, 4, 7, 0, 6],
[0, 0, 0, 2, 0, 5, 8, 0, 1],
[0, 9, 0, 7, 4, 0, 5, 0, 0],
[0, 0, 0, 0, 0, 3, 0, 7, 0],
[7, 4, 0, 0, 0, 0, 0, 0, 0],
[3, 0, 0, 9, 5, 0, 6, 0, 0],
[0, 0, 6, 4, 0, 0, 0, 1, 3],
[1, 7, 0, 0, 0, 0, 0, 0, 4]]
↓結果
6
[[9, [3, 6], [2, 3, 7], 8, 1, [6, 7], [3, 4], [3, 4], 5],
[8, 1, 5, 3, 9, 4, 7, 2, 6],
[[4, 6], [3, 6], [3, 7], 2, [6, 7], 5, 8, [3, 4, 9], 1],
[[2, 6], 9, [1, 2, 3, 8], 7, 4, [2, 6], 5, [3, 6], [2, 8]],
[[2, 6], [5, 6], [1, 2, 8], [1, 5], [2, 6, 8], 3, [1, 4], 7, [2, 8, 9]],
[7,
4,
[1, 2, 3, 8],
[1, 5],
[2, 6, 8],
[2, 6, 9],
[1, 3],
[3, 6, 9],
[2, 8, 9]],
[3, 2, 4, 9, 5, 1, 6, 8, 7],
[5, 8, 6, 4, [2, 7], [2, 7], 9, 1, 3],
[1, 7, 9, 6, 3, 8, 2, 5, 4]]
ダメかぁ。
2，7，9行目なんかは全部解けてるし、結構いい線いってますけどね。
どうやらこれだけでは候補を絞り切れないようです。
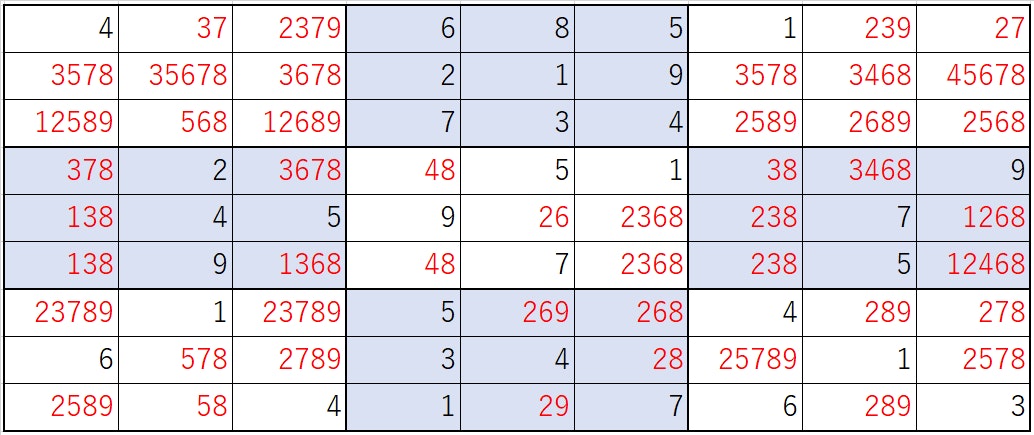
この結果を表で表すと以下のような感じでしょうか。
赤字は候補としています。
さて、そこそこ埋まっているのでもう一息という感じですが、どうやって解きましょう。
自分で解くとすると・・・
例えば1列目3行目の「46」であれば、ブロック内の他のセルで「4」を候補に持つものがないので、答えが「4」に決められる、といった感じでしょうか。
他のセルの候補と比較して答えを見つける関数
セルの候補を絞った後、縦・横・ブロック内のセルの候補と比較します。
比較した結果、ほかのセルにない候補があればそれを答えとする関数を作ります。
itertools を使うのでインポートしておきましょう。
sudoku.ipynb
import itertools
まずは縦方向のセルから。
sudoku.ipynb
def generate_possible_ver(x, y, list_sudoku):
"""
縦方向のセルの候補を収集する
"""
list_ver = [list_sudoku[i][x] for i in range(9) if type(list_sudoku[i][x]) is list and i!=y]
return set(itertools.chain.from_iterable(list_ver))
続いて横。
sudoku.ipynb
def generate_possible_hor(x, y, list_sudoku):
"""
横方向のセルの候補を収集する
"""
list_hor = [list_sudoku[y][i] for i in range(9) if type(list_sudoku[y][i]) is list and i!=x]
return set(itertools.chain.from_iterable(list_hor))
そしてブロック内。
sudoku.ipynb
def generate_possible_blo(x, y, list_sudoku):
"""
ブロック内のセルの候補を収集する
"""
index_x = (x // 3) * 3
index_y = (y // 3) * 3
list_blo = [list_sudoku[i][j] for i in range(index_y, index_y+3) for j in range(index_x, index_x+3) if type(list_sudoku[i][j]) is list and (i!=y or j!=x)]
return set(itertools.chain.from_iterable(list_blo))
候補と比較して、唯一の候補があればセルに代入する関数を作ります。
sudoku.ipynb
def find_only_one(x, y, list_possible, list_sudoku):
"""
縦・横・ブロック内のセルの候補と比較し、
他のセルにない候補があれば、答えとする
"""
diff_ver = set(list_possible) - generate_possible_ver(x, y, list_sudoku)
if len(diff_ver) == 1:
return list(diff_ver)[0]
diff_hor = set(list_possible) - generate_possible_hor(x, y, list_sudoku)
if len(diff_hor) == 1:
return list(diff_hor)[0]
diff_blo = set(list_possible) - generate_possible_blo(x, y, list_sudoku)
if len(diff_blo) == 1:
return list(diff_blo)[0]
return list_possible
↑をすべてのセルに対して実行する関数を作ります。
もちろん答えがすでに出ているやつはスルーで。
sudoku.ipynb
def try_solve(list_sudoku):
"""
まだ答えが確定していないセルに対し、
narrow()とfind_only_one()を実行する
"""
for y in range(9):
for x in range(9):
if list_sudoku[y][x] != 0 and type(list_sudoku[y][x]) is int:
continue
else:
list_sudoku[y][x] = narrow(x, y, list_sudoku[y][x], list_sudoku)
list_sudoku[y][x] = find_only_one(x, y, list_sudoku[y][x], list_sudoku)
if type(list_sudoku[y][x]) is list and len(list_sudoku[y][x]) == 1:
list_sudoku[y][x] = list_sudoku[y][x][0]
return list_sudoku
では早速試してみましょう！
Medium を解いてみる
今回も temp_sudoku と比較して変化がなければ終了ということにします。
sudoku.ipynb
import copy
list_possible = [i for i in range(1, 10)]
count = 0
temp_sudoku = []
while(True):
temp_sudoku = copy.deepcopy(list_sudoku)
count += 1
list_sudoku = try_solve(apply_narrow(list_sudoku))
if temp_sudoku == list_sudoku:
break
print(count)
list_sudoku
↓出力結果
4
[[9, 6, 2, 8, 1, 7, 3, 4, 5],
[8, 1, 5, 3, 9, 4, 7, 2, 6],
[4, 3, 7, 2, 6, 5, 8, 9, 1],
[2, 9, 1, 7, 4, 6, 5, 3, 8],
[6, 5, 8, 1, 2, 3, 4, 7, 9],
[7, 4, 3, 5, 8, 9, 1, 6, 2],
[3, 2, 4, 9, 5, 1, 6, 8, 7],
[5, 8, 6, 4, 7, 2, 9, 1, 3],
[1, 7, 9, 6, 3, 8, 2, 5, 4]]
良さそうですね。
この調子で Hard も行っちゃいましょう。
Hard を解いてみる
sudoku.ipynb
# hard
list_sudoku = [
[1, 3, 0, 6, 0, 0, 0, 8, 0],
[0, 4, 6, 0, 3, 0, 0, 0, 0],
[0, 2, 0, 5, 0, 0, 0, 0, 0],
[0, 0, 0, 2, 0, 0, 1, 0, 6],
[0, 9, 0, 0, 5, 7, 0, 0, 0],
[8, 0, 0, 0, 0, 0, 0, 4, 5],
[0, 0, 0, 0, 0, 0, 3, 7, 0],
[0, 0, 0, 0, 6, 3, 4, 0, 0],
[0, 0, 0, 0, 0, 0, 5, 0, 1]]
↓結果
4
[[1, 3, 5, 6, 7, 2, 9, 8, 4],
[9, 4, 6, 8, 3, 1, 2, 5, 7],
[7, 2, 8, 5, 4, 9, 6, 1, 3],
[3, 5, 7, 2, 8, 4, 1, 9, 6],
[6, 9, 4, 1, 5, 7, 8, 3, 2],
[8, 1, 2, 3, 9, 6, 7, 4, 5],
[2, 6, 9, 4, 1, 5, 3, 7, 8],
[5, 8, 1, 7, 6, 3, 4, 2, 9],
[4, 7, 3, 9, 2, 8, 5, 6, 1]]
できましたね！
もしかしたらこの世の数独はすべてこのロジックで解けるんじゃないでしょうか？
Expert も試してみましょう！
sudoku.ipynb
# expert
list_sudoku = [
[4, 0, 0, 0, 8, 0, 1, 0, 0],
[0, 0, 0, 2, 0, 9, 0, 0, 0],
[0, 0, 0, 7, 3, 0, 0, 0, 0],
[0, 2, 0, 0, 0, 1, 0, 0, 9],
[0, 0, 5, 0, 0, 0, 0, 7, 0],
[0, 9, 0, 0, 0, 0, 0, 5, 0],
[0, 1, 0, 5, 0, 0, 4, 0, 0],
[6, 0, 0, 3, 0, 0, 0, 0, 0],
[0, 0, 4, 0, 0, 7, 6, 0, 3]]
↓結果
3
[[4, [3, 7], [2, 3, 7, 9], 6, 8, 5, 1, [2, 3, 9], [2, 7]],
[[3, 5, 7, 8],
[3, 5, 6, 7, 8],
[3, 6, 7, 8],
2,
1,
9,
[3, 5, 7, 8],
[3, 4, 6, 8],
[4, 5, 6, 7, 8]],
[[1, 2, 5, 8, 9],
[5, 6, 8],
[1, 2, 6, 8, 9],
7,
3,
4,
[2, 5, 8, 9],
[2, 6, 8, 9],
[2, 5, 6, 8]],
[[3, 7, 8], 2, [3, 6, 7, 8], [4, 8], 5, 1, [3, 8], [3, 4, 6, 8], 9],
[[1, 3, 8], 4, 5, 9, [2, 6], [2, 3, 6, 8], [2, 3, 8], 7, [1, 2, 6, 8]],
[[1, 3, 8],
9,
[1, 3, 6, 8],
[4, 8],
7,
[2, 3, 6, 8],
[2, 3, 8],
5,
[1, 2, 4, 6, 8]],
[[2, 3, 7, 8, 9],
1,
[2, 3, 7, 8, 9],
5,
[2, 6, 9],
[2, 6, 8],
4,
[2, 8, 9],
[2, 7, 8]],
[6, [5, 7, 8], [2, 7, 8, 9], 3, 4, [2, 8], [2, 5, 7, 8, 9], 1, [2, 5, 7, 8]],
[[2, 5, 8, 9], [5, 8], 4, 1, [2, 9], 7, 6, [2, 8, 9], 3]]
はい。全然だめでした。
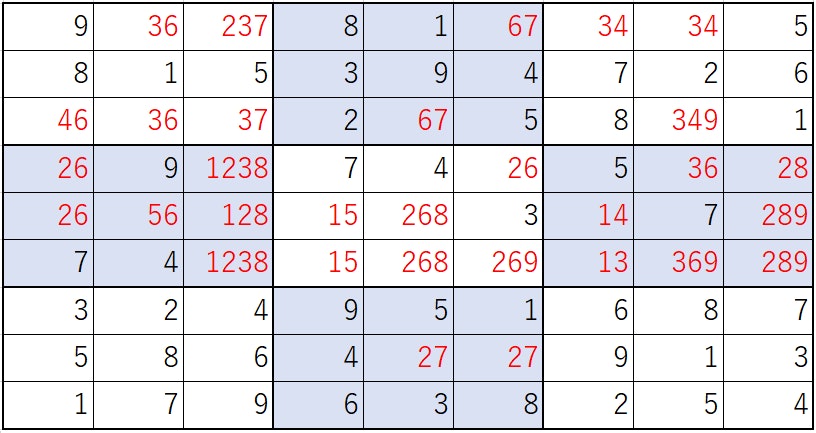
表にするとこんな感じでしょうか。
さすが Expert レベル。全然解けてません。
さらに困ったことに、私の数独力では全く解ける気がしません。どうしましょう。
総当たりで解く関数
仕方ないので総当たりで順番に全部試していきます。
再帰的に入れていけばできそうです。
まずは重複チェックの関数。
総当たりで解くとは言え、既に入らないとわかっている数字は試さなくて済みますからね。
sudoku.ipynb
def dup_check(x, y, possible, list_sudoku):
"""
縦・横・ブロック内のセルに、
すでに重複する値が入っていないかチェック
"""
for pos in range(9):
if list_sudoku[y][pos] == possible or list_sudoku[pos][x] == possible:
return False
index_x = (x // 3) * 3
index_y = (y // 3) * 3
for pos_y in range(index_y, index_y+3):
for pos_x in range(index_x, index_x+3):
if list_sudoku[pos_y][pos_x] == possible:
return False
return True
そして総当たりで解く関数。
解けない問題とかあると無限ループしちゃうので、時間制限(60秒)を設けています。
秒数は適当。
sudoku.ipynb
def brute_force(list_sudoku, list_ans, x=0, y=0):
"""
総当たりで解いてみる
60秒以上かかるのであれば解けないと判断
"""
if type(list_sudoku[y][x]) is list:
time_process = time.time()
if (time_process - time_start) >= 60:
return False
for possible in list_sudoku[y][x]:
if dup_check(x, y, possible, list_ans):
list_ans[y][x] = possible
if x <= 7:
next_x = x + 1
next_y = y
elif y <= 7:
next_x = 0
next_y = y + 1
else:
return True
if not brute_force(list_sudoku, list_ans, next_x, next_y):
continue
else:
return True
list_ans[y][x] = []
return False
else:
list_ans[y][x] = list_sudoku[y][x]
if x <= 7:
next_x = x + 1
next_y = y
elif y <= 7:
next_x = 0
next_y = y + 1
else:
return True
return brute_force(list_sudoku, list_ans, next_x, next_y)
Expert を解いてみる
さてどうでしょう？
sudoku.ipynb
import copy
import time
time_start = time.time()
temp_sudoku = copy.deepcopy(list_sudoku)
list_ans = [[[] for i in range(9)] for j in range(9)]
result = brute_force(temp_sudoku, list_ans)
print(result)
list_ans
↓出力結果
True
[[4, 7, 9, 6, 8, 5, 1, 3, 2],
[5, 3, 8, 2, 1, 9, 7, 6, 4],
[1, 6, 2, 7, 3, 4, 5, 9, 8],
[7, 2, 6, 8, 5, 1, 3, 4, 9],
[3, 4, 5, 9, 2, 6, 8, 7, 1],
[8, 9, 1, 4, 7, 3, 2, 5, 6],
[9, 1, 3, 5, 6, 8, 4, 2, 7],
[6, 8, 7, 3, 4, 2, 9, 1, 5],
[2, 5, 4, 1, 9, 7, 6, 8, 3]]
解けた！やったぜ！
最後に
どうにか総当たり以外のロジックで解きたかったところですが、普通に解くこともできないのだから実装できるはずもなく。
「数独 解き方 上級」などで検索するといろいろ出てくるんですが、どれを参考にしてもなお解けず。。
できればいずれ何とかしたいところ。
参考
総当たりに関しては以下を参考にしています。
・Pythonで数独を解く
ついでに
画面をつけて試せるようにしてみました。
SUDOKU SOLVER