前置き
今日は、Pythonを使ってユーザーが三角形の3辺を入力したら、直角三角形になるかならないかを判定するプログラムコードの作成に着手しました。
三平方の定理(ピタゴラスの定理)とは
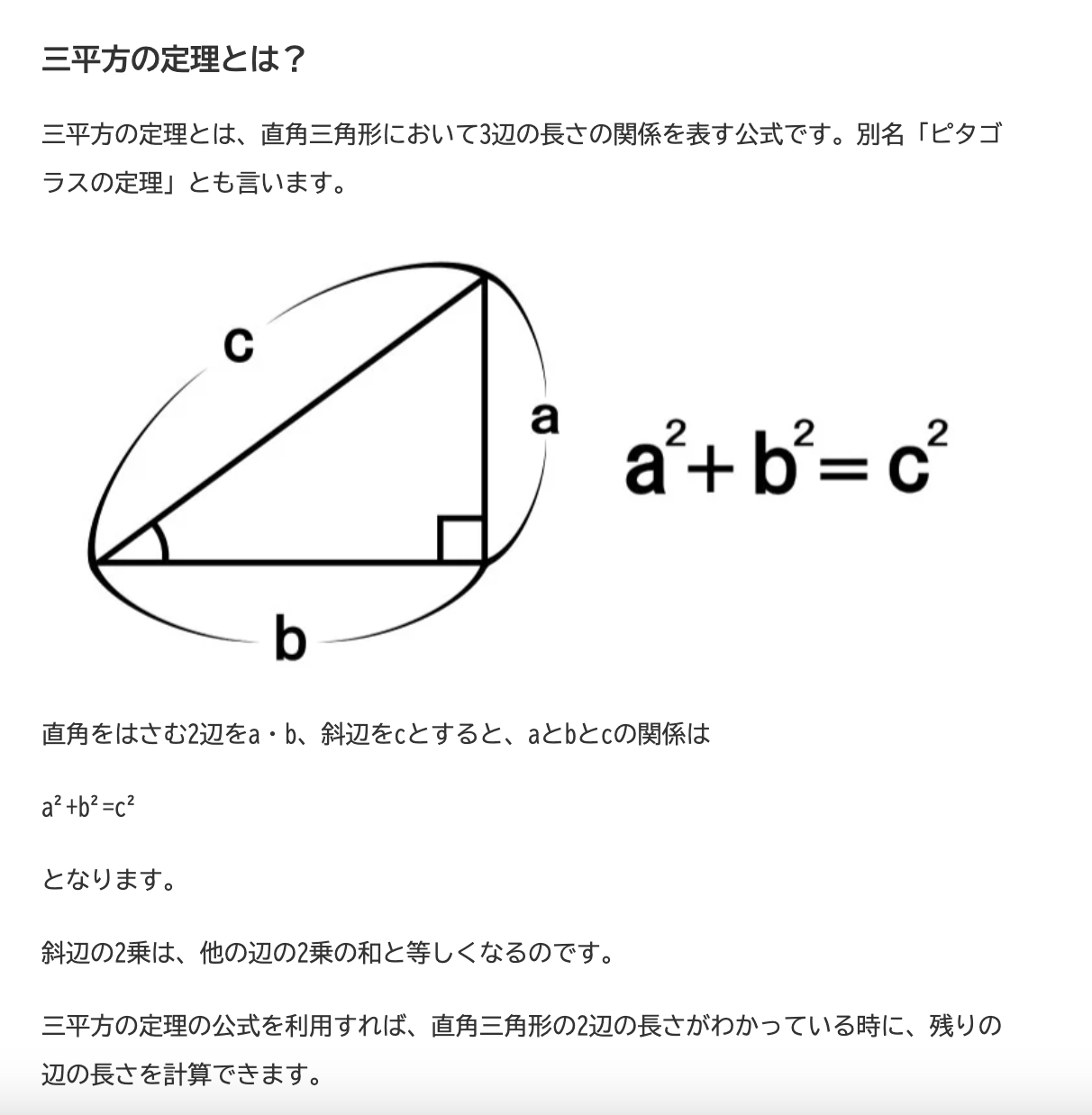
引用元:https://lab-brains.as-1.co.jp/enjoy-learn/2023/03/44327/
直角三角形かどうかを判定するプログラムコード
import math
def is_right_triangle(a, b, c):
# 3辺の長さを昇順にソートして、最長の辺をcにする
sides = sorted([a, b, c])
a, b, c = sides[0], sides[1], sides[2]
# ピタゴラスの定理を使って直角三角形かどうかを判定
return math.isclose(a**2 + b**2, c**2)
def main():
print("三角形の3辺の長さを入力してください。")
a = float(input("aの長さ: "))
b = float(input("bの長さ: "))
c = float(input("cの長さ: "))
if is_right_triangle(a, b, c):
print("この三角形は直角三角形です。")
else:
print("この三角形は直角三角形ではありません。")
if __name__ == "__main__":
main()
プログラムコードの説明
-
is_right_triangle関数:
3つの辺の長さ、a, b, c を使って最長の辺をcとしています。
ピタゴラスの定理、a^2+b^2 = c^2に沿って、その三角形が直角三角形かどうかを判定しています。
math.isclose 関数を使って、浮動小数点の誤差を考慮した近似比較を行います。 -
main関数:
ユーザーに三角形の3つの辺の長さを入力させます。
is_right_triangle関数を使って、入力された長さから直角三角形かどうかを判定し、
判定した結果を表示します。
このプログラムを使えば、その三角形が直角三角形かどうかが簡単に判定できます。
出力結果
三角形の3辺の長さを入力してください。
aの長さ: 3
bの長さ: 4
cの長さ: 5
この三角形は直角三角形です。
三角形の3辺の長さを入力してください。
aの長さ: 5
bの長さ: 12
cの長さ: 13
この三角形は直角三角形です。
三角形の3辺の長さを入力してください。
aの長さ: 8
bの長さ: 15
cの長さ: 17
この三角形は直角三角形です。
三角形の3辺の長さを入力してください。
aの長さ: 7
bの長さ: 24
cの長さ: 25
この三角形は直角三角形です。
三角形の3辺の長さを入力してください。
aの長さ: 10
bの長さ: 12
cの長さ: 13
この三角形は直角三角形ではありません。
三角形の3辺の長さを入力してください。
aの長さ: 13
bの長さ: 17
cの長さ: 19
この三角形は直角三角形ではありません。
三角形の3辺の長さを入力してください。
aの長さ: 17
bの長さ: 9
cの長さ: 23
この三角形は直角三角形ではありません。
出力結果の検証
1. a = 3, b = 4, c = 5
3^2 + 4^2 = 5^2
9 + 16 = 25
この場合、a^2+b^2 = c^2になるので、直角三角形です。
2. a = 5, b = 12, c = 13
5^2 + 12^2 = 13^2
25 + 144 = 169
この場合、a^2+b^2 = c^2になるので、直角三角形です。
3. a = 8, b = 15, c = 17
8^2 + 15^2 = 17^2
64 + 225 = 289
この場合、a^2+b^2 = c^2になるので、直角三角形です。
4. a = 7, b = 24, c = 25
7^2 + 24^2 = 25^2
49 + 576 = 625
この場合、a^2+b^2 = c^2になるので、直角三角形です。
5. a = 10, b = 12, c = 13
10^2 + 12^2 = 13^2
100 + 144 = 244
a^2とb^2の和である244とc^2の和である169は等しい値でないので、
a^2+b^2 =c^2 が成立しません。
よって、この場合においては、直角三角形になりません
6. a = 13, b = 17, c = 19
13^2 + 17^2 = 19^2
169 + 289 = 458
a^2とb^2の和である458とc^2の和である361は等しい値でないので、
a^2+b^2 =c^2 が成立しません。
よって、この場合においては、直角三角形になりません
7. a = 17, b = 9, c = 23
17^2 + 9^2 = 23^2
289 + 81 = 370
a^2とb^2の和である370とc^2の和である529は等しい値でないので、
a^2+b^2 =c^2 が成立しません。
よって、この場合においては、直角三角形になりません
このように、ちゃんと出力結果と三平方の定理に照らし合わせた場合、計算結果が一致します。
主なピタゴラス数と、覚え方について
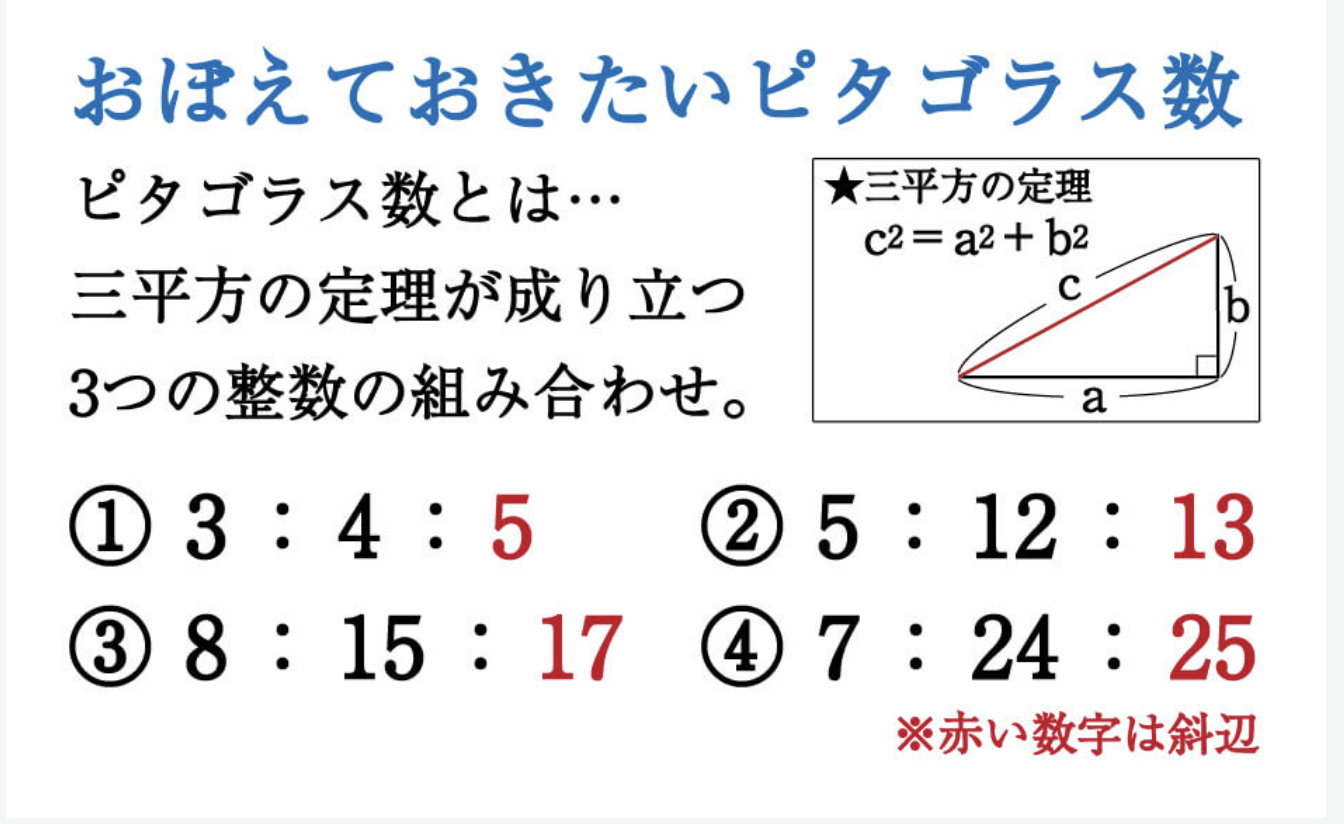

引用元:https://www.shuei-yobiko.co.jp/labo/jh-math-byousatsu05/
皆さんも時間がある時に、このプログラムコードを参考にして、ご自身が入力した三角形の3辺が、直角三角形になるか、ならないのかを判定してみてはいかがでしょうか。