はじめに
この記事は、3点の座標を元にそれらの点が作り出す角の大きさと、点の順序が決まっている際の角の回転方向を求める方法を紹介します。
何に使うのか?
以前に4つの点が与えられた際に出来上がる図形についての記事(リンク)を書きましたが、座標空間上で図形を得た後に出来る事柄の一つとして、
・図形を構成する点以外の点が図形の中にあるのか外にあるのかを判定
というものがあります。
この「内外判定」の手法に一つに「Winding Number Algorithm」という手法があり、以下の手順で内外判定を行います。
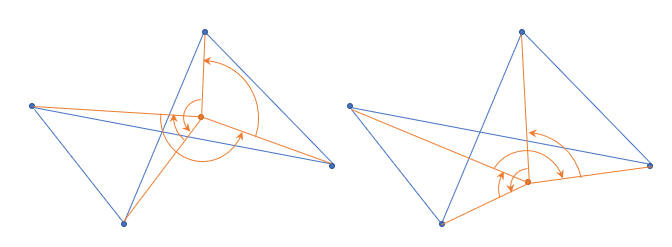
- 内外判定を行いたい点 $ P $ と対象となる領域の頂点 $ V_0, V_1, ..., V_n $ をそれぞれ線で結ぶ。
- 反時計回りを正、時計回りを負として$ ∠V_0PV_1, ∠V_1PV_2, ..., ∠V_{n-1}PV_n, ∠V_nPV_0 $ の合計 $ wn $ を計算する。
- $ wn \geq 2\pi $ の場合、点 $ P $ の周りを図形が取り囲んでいることになるので内側の判定となる。逆に、外側となる場合は角度が相殺されるので $ wn = 0 $ となる。
※詳しい内容や境界に点が存在する場合などについては話が逸れるため、自身で調べてみてください。
この手順の2.で触れている手順を実行するために点の座標から角の大きさと回転方向の二つを計算する必要があります。
角の大きさを求める
角の大きさの求め方としては、$ arcsin(x), arccos(x), arctan(x) $ などが存在します。
今回は点の座標が分かっているため、ベクトルから算出できる $ cosθ $ を用いて $ arccos(cosθ) $ で角度を求めます。
例として、点$ P, V_0, V_1 $の座標を$ (1, 1), (3, 1), (2, 2) $とした際の$ ∠V_0PV_1 $について計算してみます。
まずは、$\vec{V_0P}, \vec{V_1P}$ を求めます。
\vec{PV_0}=(3-1, 1-1)=(2, 0) \\
\vec{PV_1}=(2-1, 2-1)=(1, 1)
ベクトル $ \vec{a}, \vec{b}$ がなす角$ θ $ の $ cosθ$ は
cosθ=\frac{\vec{a}⋅\vec{b}}{|\vec{a}||\vec{b}|}
で求めることができるため、$ cos∠V_0PV_1 $は、
cos∠V_0PV_1=\frac{\vec{PV_0}⋅\vec{PV_1}}{|\vec{PV_0}||\vec{PV_1}|} \\
=\frac{2⋅1+0⋅1}{\sqrt{2^2+0^2}\sqrt{1^2+1^2}} \\
=\frac{2}{2\sqrt{2}} \\
=\frac{1}{\sqrt{2}}
となります。
ここから更に $ arccos(cosθ)$ を計算する必要がありますが、実際の $ cosθ $ は角の大きさを綺麗に計算できる値でないことの方が圧倒的なため、お使いのプログラミング言語に存在する $ arccos $ の関数を用いることになります。
角の回転方向を求める
今度は角の回転方向が反時計回り(+方向)なのか時計回り(-方向)なのかを求めます。
2つの3次元ベクトル $\vec{a}, \vec{b}$ から得られる外積 $\vec{a}×\vec{b}$ もまた3次元ベクトルであり、その特徴として、
・$\vec{a}, \vec{b}$ の双方と直行する
・$\vec{a}, \vec{b}$ からなる平面に対する向きは右ネジの法則で決まる
が挙げられます。
その為、図形を構成する点や内外判定の対象とする点が3次元空間上の $z=0$ の平面に存在するものと考えると、$ ∠V_{n-1}PV_n $ について、上記の特徴を以下の様に読み替えられます。
・$\vec{PV_{n-1}}×\vec{PV_n}$ はZ軸に対して並行なベクトルとなる(= x 座標、y 座標がそれぞれ 0 になる)
・角が反時計回りの場合は z の値は正の値になり、角が時計回りの場合は z の値は負の値になる
よって、$\vec{PV_{n-1}}×\vec{PV_n}$ の z 座標の値を計算し、その値の正負をそのまま角の回転方向として扱うことができることが分かります。
先ほどの例の点$ P, V_0, V_1 $を用いると、
\vec{PV_0}×\vec{PV_1}=(0⋅0-0⋅1, 0⋅1-2⋅0, 2⋅1-0⋅1) \\
=(0,0,2)
となるので、$ ∠V_0PV_1 $ が反時計回りであることと z 座標の値の正負が一致しています。
追記(12/28追加):境界条件の検討
今回の内容でベクトルの内積、絶対値、外積を用いましたが、内外判定の対象となる点がランダムに与えらえる都合上、考慮すべき事項がいくつか存在します。
1. 点が領域の頂点と重なる場合
点$ P $が領域のある頂点$ V_k $と重なる場合、$ \vec{PV_k} = (0, 0) $ となるため、$ |\vec{PV_k}| = 0 $ となります。
ベクトルの絶対値が 0 となる場合、$ cosθ $ を解散する過程で分母が 0 となるため、角の大きさを計算することが不可能になります。
よって、点が領域の頂点と重なる場合には内と外のどちらに判定するかを事前に決めておき、アルゴリズム上で対象の点が頂点と同じ座標かどうかを検証して同じ座標と判別できた時点で判定を出す必要があります。
2. 点が領域の辺上に存在する場合
点$ P $が領域のある辺$ V_kV_{k+1} $上に存在する場合、外積を導くためのベクトルが逆方向となるため、$ \vec{PV_k}×\vec{PV_{k+1}} = (0, 0, 0) $となります。
外積のz座標の値が 0 となる以上、角の回転方向については反時計回りと時計回りのどちらに捉えることも可能です。
角の回転方向がどちらとも取れる都合上、$ wn $ の値は 0 にも $ 2\pi $ のどちらにもすることができるため、点が領域の辺上に存在する場合にも内と外のどちらに判定するかを事前に決めておき、外積のz座標の値が0となった時点で判定を出す必要があります。