この記事はlotzさんの「動的計画法を実現する代数〜トロピカル演算でグラフの最短経路を計算する〜」という記事を読んで、自分の問題に対しても応用できないかと考えた結果をまとめたものです。
先に元の記事を読んでから以下の内容を読んで頂けるとスムーズかと思われます。
最長交易路とは
皆様は『カタン』というゲームをご存知でしょうか?
カタンは複数のプレイヤーが無人島を開拓して、最も繁栄させることができたプレイヤーが勝利するというボードゲームです。
このゲームには「最長交易路」というルールがあり、最も長い交易路を作ったプレイヤーに追加の得点が入ることになっています。
このゲームにおける交易路はグラフ理論の言葉を借りると無向多重グラフとみなすことができます。
そして、最長交易路を探すということは、無向多重グラフの中で最長の**小道(trail)**を探すことになります。
ここでは、ある頂点からある頂点へ行くルートのうち、頂点の反復を許して辺の反復を許さないようなルートのことを小道と呼んでいます。
最長交易路を探すのって面倒くさい
最長交易路を探すアルゴリズムを考えるのは中々に面倒くさいです。
少し探してみると、 Stack Overflow で最長交易路を探すアルゴリズムについての議論を見つけました。
ここで示されている方法は「全ての行き止まりや三叉路から、辺の重複を許さないように幅優先or深さ優先探索をする」というもので、これまた中々に実装が面倒くさそうです。
議論の中でこの問題はNP困難だと指摘されているので、計算量を減らすことは難しいと思われます。
しかし、実装の手間という面で見たときに何かもっとシンプルな方法はないでしょうか?
代数の力を借りる
そんなことを考えているときに、冒頭で紹介した記事を見つけました。
隣接行列や重み行列を使ったアルゴリズムとしては、重みなしグラフの道を数えるアルゴリズムや、一次元Isingモデルの厳密解を求める方法などが有名です。
冒頭の記事では通常の足し算と掛け算ではないような半環を考えることで、これらのアルゴリズムと同じ考え方が非常に幅広い応用範囲を持つということが紹介されていました。
代数ってすごいなぁ。。。
そして、最長交易路の探索問題にもこれを応用できないかと考えました。
小道を探索するための半環を定義する
まず、以下のように頂点と辺と小道を定義します。
type Node = Char
data Edge = Edge Node Node
instance Show Edge where
show (Edge n1 n2) = n1 : '-' : [n2]
instance Eq Edge where
(==) (Edge n1 n2) (Edge n3 n4) =
(n1 == n3 && n2 == n4) || (n1 == n4 && n2 == n3)
type Trail e = [e]
newtype TrailList e = TL [Trail e] deriving Show
後述する理由から小道そのものではなく小道のリストを半環にして、各頂点から頂点へ続く小道を全て保存するようにします。
半環にする
ここに加法、乗法、それぞれの単位元を定義して半環にします。
instance Eq e => Semiring (TrailList e) where
oplus (TL a) (TL b) = TL $ a ++ b
zero = TL []
otimes (TL a) (TL b) =
TL $ nub [a' ++ b' | a' <- a, b' <- b, disjoint a' b']
one = TL [[]]
disjoint :: Eq a => [a] -> [a] -> Bool
disjoint [] _ = True
disjoint _ [] = True
disjoint (x:xs) ys =
not (elem x ys) && disjoint xs ys
disjointは2つのリストの要素に重複がないときにTrueを返す関数です。
加法は小道のリストを結合する演算で、乗法はリスト内の小道を連結する演算です。
なぜ長い小道だけを選ばないのか
なぜ加法を、冒頭の記事のように長い道だけを選ぶ実装にしないのでしょう?
それは今回の問題では考える対象が小道であることに関係します。
例えば、以下の図のようなグラフに対して、隣接行列をつくることを考えます。
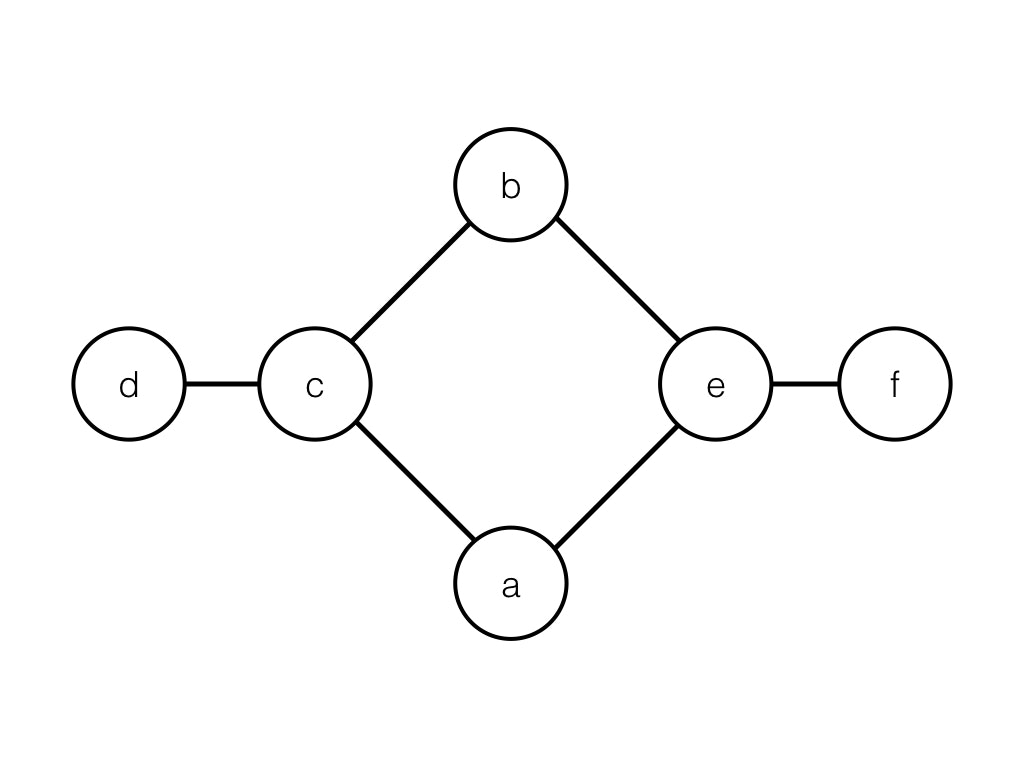
このグラフの隣接行列を$A$として、$A^2 \cdot A^2 = A^4$について考えます。
$A^4$のa行d列目にはa→e→b→c→dという小道が入っていることが期待されます。
そのためには$A^2$のa行b列目には、この小道の前半部分であるa→e→bが入っている必要があります。
同様に$A^4$のa行f列目には a→c→b→e→fという小道が入っていることが期待されるので、$A^2$のa行b列目はこの小道の前半部分である a→c→b が入っている必要があります。
つまり$A^2$のa行b列目には a→c→bという小道と a→e→b という小道の両方が入っている必要があります。
そのため、どちらか片方を選択するような加法の実装はせず、リストで候補となる小道を全て保存する実装にしました。
動かしてみる
テストとして、先程の図のグラフについて隣接行列をつくってみます。
以下、行列計算の実装については冒頭の記事のものをそのまま使わせて頂きました。
a :: Matrix (TrailList Edge)
a =
[[zero, zero, TL [[Edge 'a' 'c']], zero, TL [[Edge 'a' 'e']], zero]
,[zero, zero, TL [[Edge 'b' 'c']], zero, TL [[Edge 'b' 'e']], zero]
,[TL [[Edge 'c' 'a']], TL [[Edge 'c' 'b']], zero, TL [[Edge 'c' 'd']], zero, zero]
,[zero, zero, TL [[Edge 'd' 'c']], zero, zero, zero]
,[TL [[Edge 'e' 'a']], TL [[Edge 'e' 'b']], zero, zero, zero, TL [[Edge 'e' 'f']]]
,[zero, zero, zero, zero, TL [[Edge 'f' 'e']], zero]
]
それでは実際にaの1乗から順に計算してみます。
GHCi> mapM_ print $ a `power` 1
[TL [],TL [],TL [[a-c]],TL [],TL [[a-e]],TL []]
[TL [],TL [],TL [[b-c]],TL [],TL [[b-e]],TL []]
[TL [[c-a]],TL [[c-b]],TL [],TL [[c-d]],TL [],TL []]
[TL [],TL [],TL [[d-c]],TL [],TL [],TL []]
[TL [[e-a]],TL [[e-b]],TL [],TL [],TL [],TL [[e-f]]]
[TL [],TL [],TL [],TL [],TL [[f-e]],TL []]
GHCi> mapM_ print $ a `power` 2
[TL [],TL [[a-c,c-b],[a-e,e-b]],TL [],TL [[a-c,c-d]],TL [],TL [[a-e,e-f]]]
[TL [[b-c,c-a],[b-e,e-a]],TL [],TL [],TL [[b-c,c-d]],TL [],TL [[b-e,e-f]]]
[TL [],TL [],TL [],TL [],TL [[c-a,a-e],[c-b,b-e]],TL []]
[TL [[d-c,c-a]],TL [[d-c,c-b]],TL [],TL [],TL [],TL []]
[TL [],TL [],TL [[e-a,a-c],[e-b,b-c]],TL [],TL [],TL []]
[TL [[f-e,e-a]],TL [[f-e,e-b]],TL [],TL [],TL [],TL []]
GHCi> mapM_ print $ a `power` 3
[TL [],TL [],TL [[a-e,e-b,b-c]],TL [],TL [[a-c,c-b,b-e]],TL []]
[TL [],TL [],TL [[b-e,e-a,a-c]],TL [],TL [[b-c,c-a,a-e]],TL []]
[TL [[c-b,b-e,e-a]],TL [[c-a,a-e,e-b]],TL [],TL [],TL [],TL [[c-a,a-e,e-f],[c-b,b-e,e-f]]]
[TL [],TL [],TL [],TL [],TL [[d-c,c-a,a-e],[d-c,c-b,b-e]],TL []]
[TL [[e-b,b-c,c-a]],TL [[e-a,a-c,c-b]],TL [],TL [[e-a,a-c,c-d],[e-b,b-c,c-d]],TL [],TL []]
[TL [],TL [],TL [[f-e,e-a,a-c],[f-e,e-b,b-c]],TL [],TL [],TL []]
GHCi> mapM_ print $ a `power` 4
[TL [[a-c,c-b,b-e,e-a],[a-e,e-b,b-c,c-a]],TL [],TL [],TL [[a-e,e-b,b-c,c-d]],TL [],TL [[a-c,c-b,b-e,e-f]]]
[TL [],TL [[b-c,c-a,a-e,e-b],[b-e,e-a,a-c,c-b]],TL [],TL [[b-e,e-a,a-c,c-d]],TL [],TL [[b-c,c-a,a-e,e-f]]]
[TL [],TL [],TL [[c-a,a-e,e-b,b-c],[c-b,b-e,e-a,a-c]],TL [],TL [],TL []]
[TL [[d-c,c-b,b-e,e-a]],TL [[d-c,c-a,a-e,e-b]],TL [],TL [],TL [],TL [[d-c,c-a,a-e,e-f],[d-c,c-b,b-e,e-f]]]
[TL [],TL [],TL [],TL [],TL [[e-a,a-c,c-b,b-e],[e-b,b-c,c-a,a-e]],TL []]
[TL [[f-e,e-b,b-c,c-a]],TL [[f-e,e-a,a-c,c-b]],TL [],TL [[f-e,e-a,a-c,c-d],[f-e,e-b,b-c,c-d]],TL [],TL []]
GHCi> mapM_ print $ a `power` 5
[TL [],TL [],TL [],TL [],TL [],TL []]
[TL [],TL [],TL [],TL [],TL [],TL []]
[TL [],TL [],TL [],TL [[c-a,a-e,e-b,b-c,c-d],[c-b,b-e,e-a,a-c,c-d]],TL [],TL []]
[TL [],TL [],TL [[d-c,c-a,a-e,e-b,b-c],[d-c,c-b,b-e,e-a,a-c]],TL [],TL [],TL []]
[TL [],TL [],TL [],TL [],TL [],TL [[e-a,a-c,c-b,b-e,e-f],[e-b,b-c,c-a,a-e,e-f]]]
[TL [],TL [],TL [],TL [],TL [[f-e,e-a,a-c,c-b,b-e],[f-e,e-b,b-c,c-a,a-e]],TL []]
GHCi> mapM_ print $ a `power` 6
[TL [],TL [],TL [],TL [],TL [],TL []]
[TL [],TL [],TL [],TL [],TL [],TL []]
[TL [],TL [],TL [],TL [],TL [],TL []]
[TL [],TL [],TL [],TL [],TL [],TL []]
[TL [],TL [],TL [],TL [],TL [],TL []]
[TL [],TL [],TL [],TL [],TL [],TL []]
このグラフには長さ6以上の小道が存在しないことがわかりました。
よって最長の小道の長さ(最長交易路)が5であることがわかります。
まとめ(感想)
自分が実装したのは半環の定義くらいです。
Stack Overflow で議論されていたような、「三叉路と行き止まりの探索や、グラフ上の深さ優先探索」といった面倒なことを全く書かずに最長交易路が求まりました。
代数ってすごいなぁ。。。