fastText の諸問題を考える

NLP（Natural Language Processing: 自然言語処理）分野における Word2Vec（単語分散表現）は、今や少なくとも BERT、一般的には Sentence-BERT 等の word-embedding 用 BERT モデルを使う時代になっているので、もはや fastText のことなんぞ誰も気にかけていないのかもしれない。

でも私は些細なことが気になると全く先に進めない厄介な人間なので、今まで悩み続けた数々の問題に曲がりなりにもここで決着をつけて、それから気持ちよく先に進んでいきたい。

例えばある文書をひとつのベクトルで表現する文書ベクトルなるものを作り、その文書ベクトルを使って文書分類などのタスクを行いたいものとする。問題はその文書ベクトルを作るまでだ。Scratch から fastText で文書ベクトルを作るまでの工程を列挙する。

（文書ベクトルを作るなら doc2vec を使えというごもっともな指摘は、ナシの方向でお願い）

• fastText の学習済みバイナリを作る
  • （問題１）コーパスの分かち書きを行うための MeCab 辞書を選ぶ
  • 日本語 Wikipedia 等の大量の文章を分かち書きして、fastText 学習用のコーパスを作る
    • この際には品詞や STOP WORD を使った単語選別を行わず、必ず全ての単語を用いる
    • （問題２）動詞などの変化形がある単語を、そのまま使うか原形に直すか
  • fastText で学習を行い、その結果を word2vec 形式のバイナリに変換して保存する
    • （問題３）ベクトルの次元数をいくつに設定するか
• 文書ベクトルを作る
  • （問題１）文書を単語に分割する MeCab 辞書を選ぶ
  • MeCab で文書（中の文章）を単語に分割する
  • （問題２）動詞などの変化形がある単語を、そのまま使うか原形に直すか
  • （問題４）名詞・動詞などの重要な品詞以外の単語を除外するかしないか
  • （問題５）STOP WORD を除外するかしないか
  • 学習済みの fastText バイナリを用いて、単語をベクトルに変換する
  • （問題６）文書中のすべての単語ベクトルを「平均」する

（問題）と付けた項目が、今回で確定させたい、つまりまだどうするか悩んでいる処理。ほとんどじゃねぇか。ほとんどなんだよ。

また、fastText の学習済みバイナリを作る所と、文書ベクトルを作る所で、共通する問題がある（問題１と問題２）。これらは当然両者で同じ方法を使うべきである。

以下に問題点のみをまとめる。

• 問題１：MeCab 辞書として何を使うべきか
• 問題２：動詞などの変化系がある単語を、そのまま使うか原形に直すか
• 問題３：ベクトルの次元数をいくつに設定するか
• 問題４：名詞・動詞などの重要な品詞以外の単語を除外するかしないか
• 問題５：STOP WORD を除外するかしないか
• 問題６：単語ベクトルを「平均」する方法とは何か

単語ベクトルの「平均」とは

上に挙げた６個の問題の内、既に（個人的に）答えが出ている問題がふたつある。問題１と問題６だ。

問題１はこの記事で考察している。この場合はUniDic（UniDic-cwj）だ。

問題６は、みんな当たり前だと思うかもしれない。

• 各ベクトルを長さ１に正規化する
• 全部のベクトルを足し合わせる
• 足し合わせた数で割り、なんならさらに長さ１に正規化する

ぶっちゃけ、これが正解だ。gensim だってこうしている。では、なぜこうしているのだろうか。

Word2Vec はふたつのベクトルの「なす角」が意味の近い・遠いを表す。cosine 距離と言っても良いし、内積と言っても良い。この際に、ベクトルの長さは「全く関係無い」。全く関係無いのに、長さ１に正規化するのはなぜなのか。

もちろん長さを１にしてしまえば、内積の値となす角 θ に対する cos θ の値が全く一致する。なので cosine 距離は 1 - 内積¹ で簡単に求められる。でも、それだけじゃない。そこが本質じゃない。

Word2Vec で重要なのは「なす角」だ。だから、単語ベクトルを平均して文書ベクトルを作るなんていう場合に、本来であれば平均したいのは「角度」だ。ベクトルの位置じゃない。だから長さ１に正規化する所が問題じゃない。「足し合わせる」箇所、ベクトルにおける各軸の位置、すなわち座標を足し算している箇所が間違っている。位置を平均したいんじゃない。角度を平均したいんだ。

じゃあ角度を平均すれば良いじゃないかと思うかもしれない。しかしこれが難しい。難しいっていうより、現実的にはほぼ不可能と言っても良い。

平均っていうことは、重心って言い換えても良い。この重心とは何かと言うと、距離の分散が最も小さくなる点だ。なので重心は距離の定義が異なると違ってくる。もちろん距離としてユークリッド距離を採用するならば、重心は算術平均（つまり普通の平均）で求められる点だ。重心を数学的に言うと「フレシェ平均」とも言える（ややこしい）。算術平均ではない平均には幾何平均や調和平均等があるが、それぞれが重心となる距離がある（フレシェ平均のリンク先である Wikipedia (en) を参照）。

じゃあ角度の重心とは何かというと、Circular Mean を考えなきゃいけない。

ぶっちゃけ、めんどい。何万個もの計算をしなきゃいけないのに、いちいちこんなことやってらんない。

じゃあどうするかというと、「角度の平均を、長さ１のベクトルの位置の平均で近似する」ということをする。そう、ここに「長さ１」の本当の意味がある。

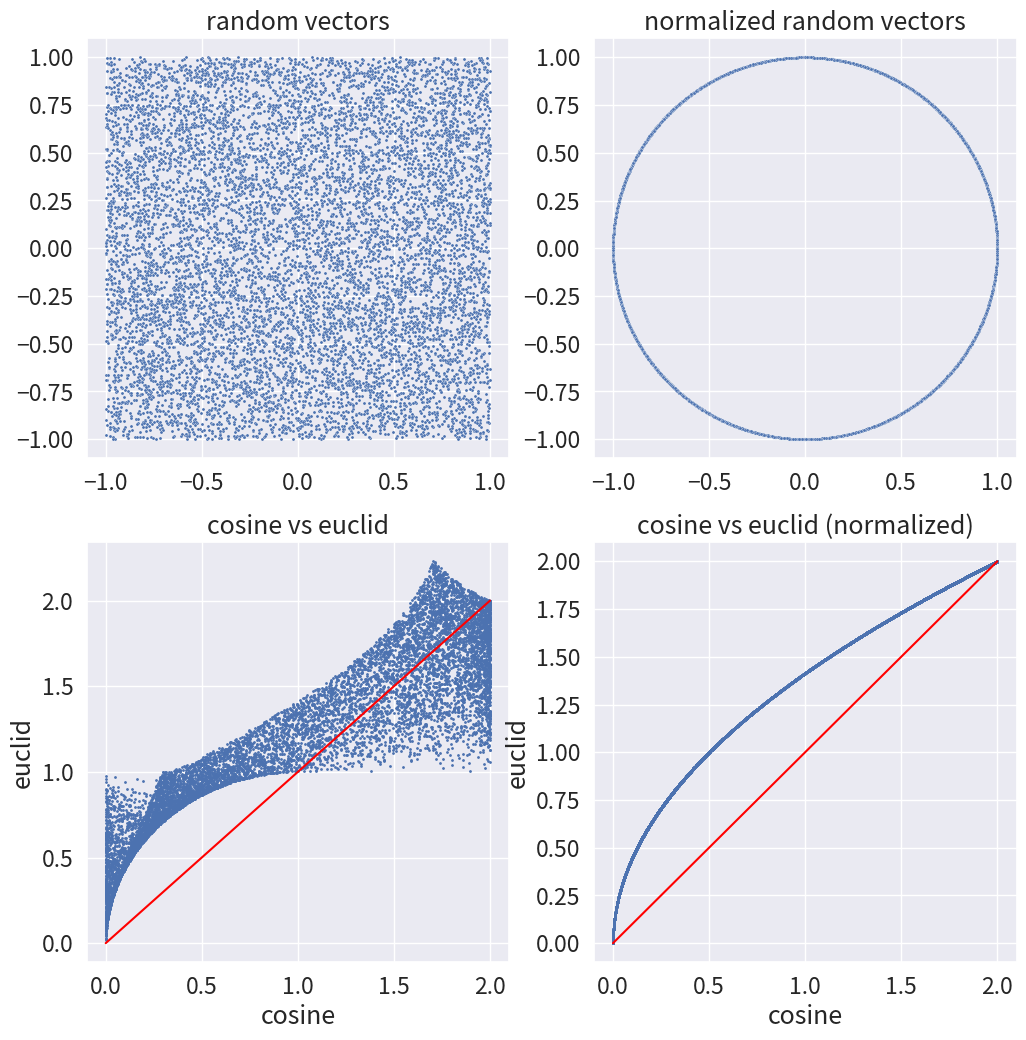
左上の図が、１万個のランダムなベクトル（点）を発生させた状態。(-1, 1) の乱数を発生させて作成している。これらのベクトルと (1, 0) のベクトルとのユークリッド距離とコサイン距離を比較したのが左下の図²。当然のことながらグチャグチャである。例えば (1, 0) の点とユークリッド距離が 1.0 の点というのは、(1, 0) から半径 1 の円周上にある点なのだが、これらの点と (1, 0) とのコサイン距離は、0.0 から 2.0 までほぼすべての領域に渡っている。

そして右上の図が、１万個のランダムなベクトルを長さ１に正規化したものである。すなわち、原点から半径１の円周上に（角度を保ちつつ）移動させたものである。これら長さ１に正規化した点において、(1, 0) からのユークリッド距離とコサイン距離の関係を示したものが右下の図である。

もちろん、長さを１に正規化しても、ユークリッド距離とコサイン距離は一致しない（y = x の赤い線上には乗らない）。しかし、少なくともユークリッド距離とコサイン距離で大小関係は保たれる。そして、言うほど y = x とは離れていない。たぶん y = sin x を y = x と近似してしまうぐらいと同じぐらいの意味で、コサイン距離は長さ１に正規化したベクトルのユークリッド距離に近似して良い！³

だから単語ベクトルの足し算は、長さ１に正規化してから普通に平均するのである。そしてその後の使いやすさを考えたら、足した後のベクトルも長さ１に正規化しておいた方が良い。

実験

ということで、問題は以下の４点に絞られた。

• 問題２：動詞などの変化系がある単語を、そのまま使うか原形に直すか
• 問題３：ベクトルの次元数をいくつに設定するか
• 問題４：名詞・動詞などの重要な品詞以外の単語を除外するかしないか
• 問題５：STOP WORD を除外するかしないか

これらをどうやって決めるかをいつも悩んでいたわけだが、今回は実験をすることで決めてしまおうというのが主旨。考えた実験は以下。

• データセットはいつもの livedoor ニュースコーパスを使わせていただく
• livedoor ニュースコーパスに収録されている各記事をベクトル化する
  • 上記４つの問題点に関して、条件を変えて様々な方法でベクトル化する
• そのベクトルがニュース媒体毎にどれだけ綺麗にまとまっているかを測る
  • ベクトルが最もばらけずにまとまっている手法が、最も良い手法

livedoor ニュースコーパスには９種類の媒体からの記事が収録されているが、このうちの「トピックニュース」はジャンルにあまり関係なくトピックが書かれているだけなので、最初から除外してある。

また、ベクトルがばらけずにまとまっているかを図る方法としては、LinearSVC で最も高いスコアが出たものを「最もまとまっている」とする。

fastText の学習

fastText の学習には日本語 Wikipedia を用いた。ここでの学習方法で問題２と問題３の条件分岐が発生する。

以降、問題２に関して、そのまま使うものを「surface」（表層形）、原形に直すものを「base」（base form: 原形）と表記する。

問題３に関してだが、一般的には Wikipedia レベルのコーパスを学習する場合は 300 次元が適切とされている⁴。しかし鈴木正敏さんの日本語 Wikipedia エンティティベクトルのページには 200 次元とある。エンティティベクトルは一般的な Word Embedding と目的が少し違うとは言え、もしかしたら日本語 Wikipedia では 300 次元よりも 200 次元の方が良いのかもしれないと迷う所である。

ということで、surfece と base、200 次元と 300 次元の合計４種類の日本語 Wikipedia 学習済み fastText バイナリ（word2vec 形式）を作成した。（これだけで数日かかった）

ベクトル次元数以外のパラメータは４種類すべて同じ、以下の値で学習した。

• model: skipgram
• epoch: 10
• ws (context window): 5 （fastText のデフォルト値）
• neg (negative sampling): 5 （fastText のデフォルト値）
• t (sampling threshold): 0.0001 （fastText のデフォルト値）
• lr (learning rate): 0.05 （fastText のデフォルト値）
• minCount: 20

学習済みの単語数は以下の通り。

• surface: 222,553
• base: 215,263

1 万個弱ほど base の方が単語数が少ない。これが原形に直した分だと考えられる。

品詞と STOP WORD

残るは問題４と問題５。

まず、問題４の品詞を取捨選択する選び方として、以下のものを想定した。

• すべて使う（all）
• 体言・用言 のみを用いる（taiyo）
  • UniDic の品詞体系で言うと、名詞・動詞・形容詞・形状詞
  • ただし、名詞.数詞 と 名詞.普通名詞.助数詞可能 は除外した
• 体言のみを用いる（taigen）
  • 要するに、名詞だけ使う
  • ただし、名詞.数詞 と 名詞.普通名詞.助数詞可能 は除外した

livedoor コーパスの各記事を分かち書きしたものに対して、surface と base の２通り x 上記の３つのパターン、すなわち６通りの単語の選び方が存在する。ただし体言は変化形も糞もないので、base のみとした。よって、５通りの単語の選び方を実装した。

次の問題５の STOP WORD である。

STOP WORD は誰かが作ってくれたもの（Slothlib 等）を使うか、自分で Document Frequency を計算して作るかの２通りがある。私はいつも後者でやっているので、今回も自分で作る。ただ、すでに５通りあるので、各々に関して細かく見ていくのはツライ。なので閾値を決めて一括でやってしまおう。

単語を数えると言えば TfidfVectorizer なので、５通りのデータをすべて TfidfVectorizer 君に突っ込む。でも TfidfVectorizer は idf しか計算してくれない不親切設計なので、idf から df を無理やり計算して、閾値をビシッと決めて、閾値以上の df を持つ単語を STOP WORD とする。

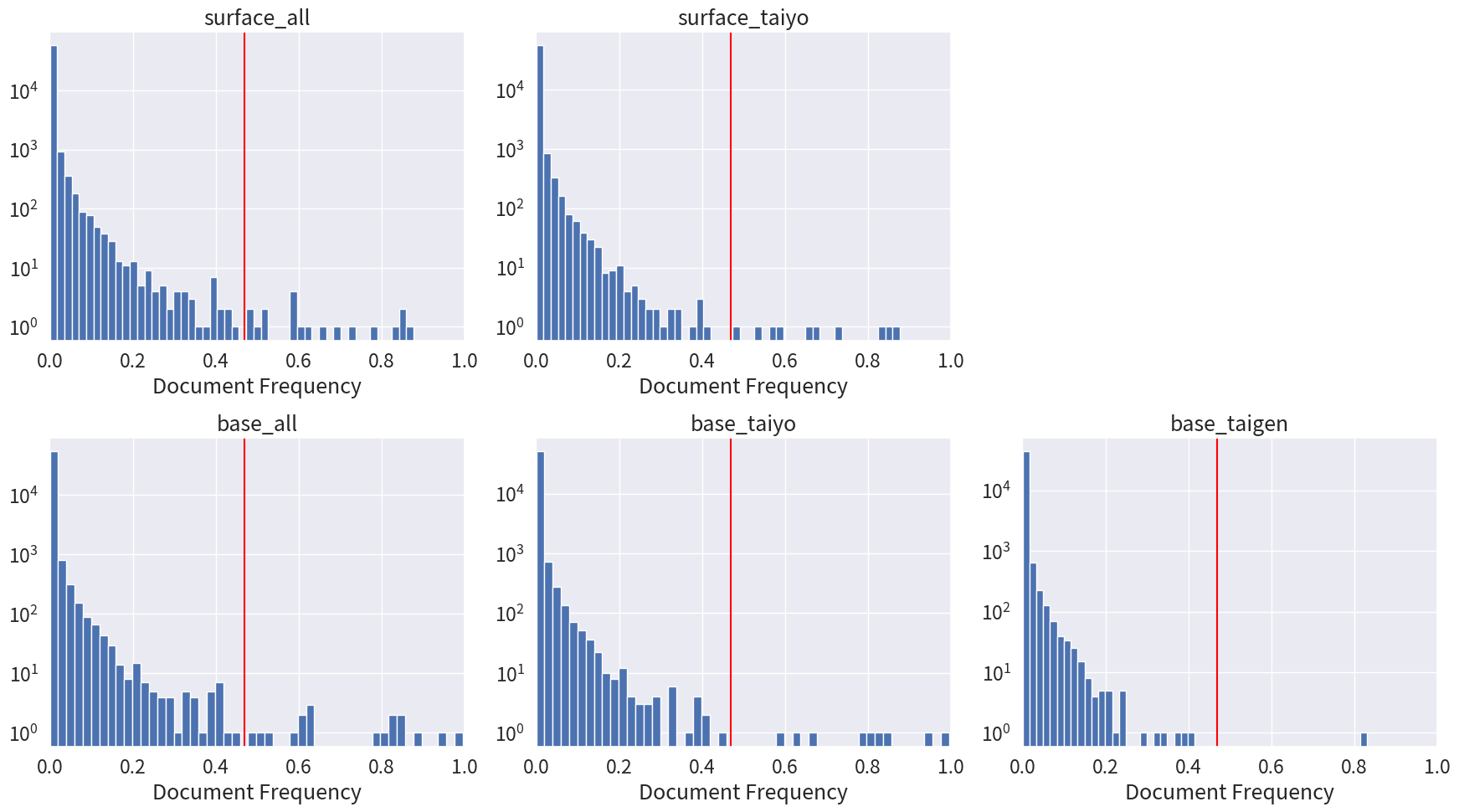
df の閾値を0.47 としたものが以下である。

ここから得られた STOP WORD は以下。

• surface_all
  • ['ある', 'いう', 'いる', 'から', 'こと', 'この', 'する', 'その', 'できる', 'です', 'ない', 'なっ', 'など', 'なる', 'ます', 'まで', 'よう', 'より', 'れる']
• surface_taiyo
  • ['ある', 'いう', 'いる', 'こと', 'する', 'できる', 'ない', 'なっ', 'なる', 'よう']
• base_all
  • ['ある', 'いう', 'いる', 'から', 'こと', 'この', 'する', 'その', 'たい', 'できる', 'です', 'ない', 'など', 'なる', 'ます', 'まで', 'よう', 'れる']
• base_taiyo
  • ['ある', 'いう', 'いる', 'こと', 'する', 'できる', 'ない', 'なる', 'よう']
• base_taigen
  • ['こと']

私はいつももっと STOP WORD を増やして単語を削ってしまうのだが、とりあえず一括で作ったにしては良いものが得られたと思う。

t-SNE で分布を見る

問題２の表層系 or 原形と問題４の品詞選択で合わせて５通り、問題５の STOP WORD の有る無しでさらに倍の１０通り、そしてそれらの各々に対して 200 次元ベクトルか 300 次元ベクトルかでさらに倍の２０通りのベクトルの作り方が有る。この２０通りのベクトルの作り方に対して、どれが一番良いかを決めていく。

自分が馬鹿なんじゃないかと思えてくるが、めげずに続ける。

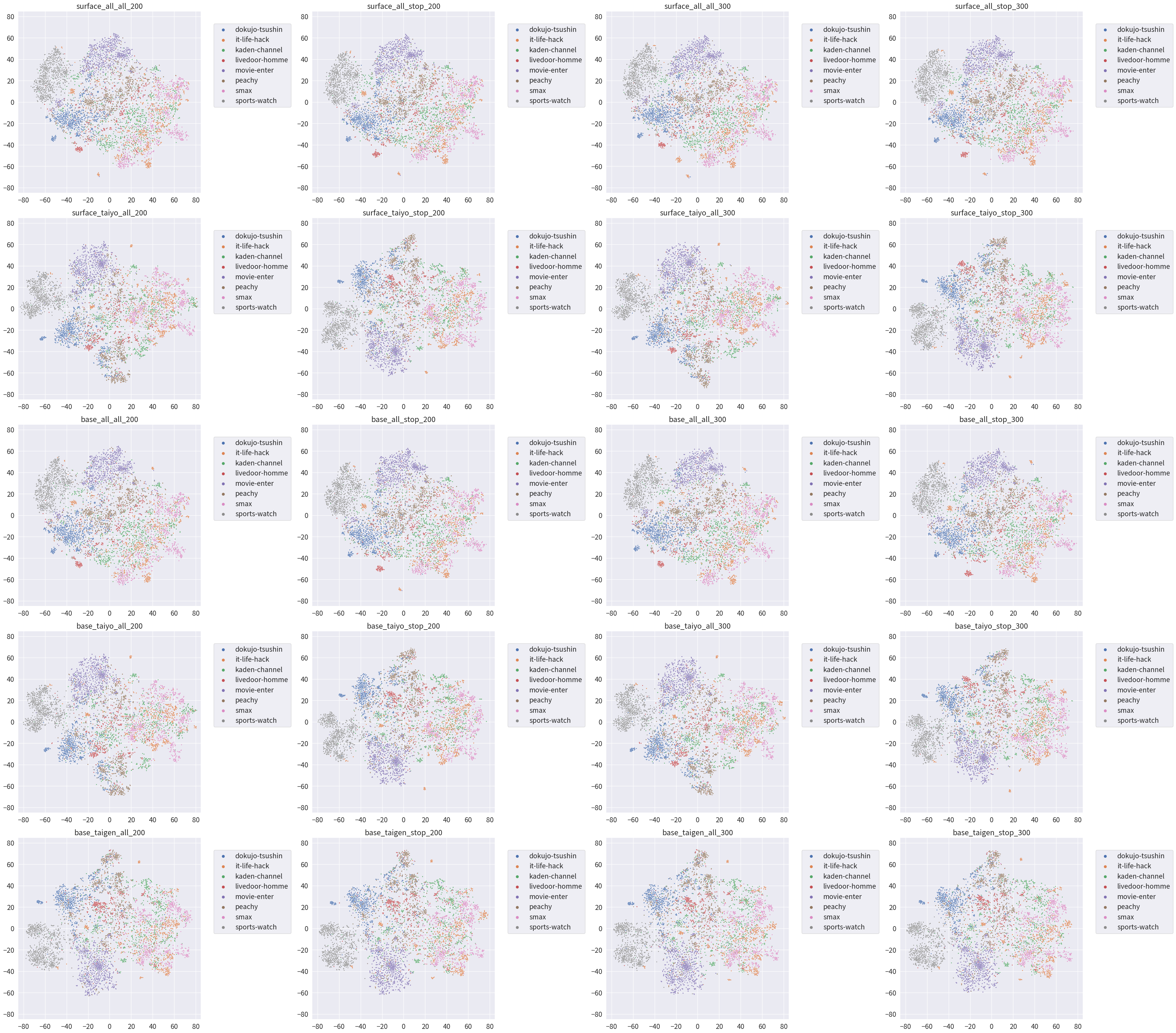
とりあえずお約束として、作った記事ベクトル（200次元 or 300次元）の分布を、t-SNE で平面に押し潰して観察してみる。

名前は [base,surface]_[all,taiyo,taigen]_[all,stop]_[200,300] という規則で付けている。

とりあえずやってみたが、「綺麗だな」以外の感想は無いね。時間かかったんだけど。

評価

いよいよ本題の、LiearSVC による評価。

今回は「ベクトルがどれだけ綺麗に揃って分布しているか」を見たいだけで、高精度に分類するモデルを作りたい訳ではない。よって、SVC のマージンを変えてしまうと訳がわからなくなってしまう。そこで、２０通りに対してすべてマージンをデフォルトの「１」に固定して学習した。

お作法通り、記事全体のうち７割を学習用、残りの３割を評価用にしてある。

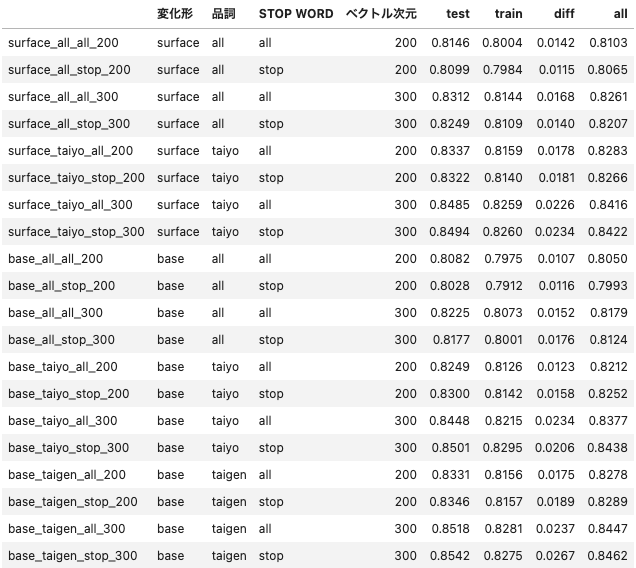
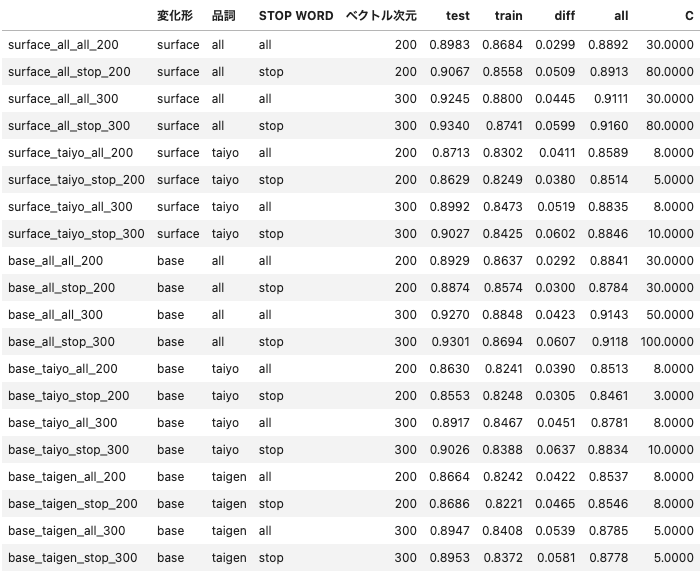
表の見方：

• 変化形：問題２で、文章に出てきたそのまま（表層形：surface）か、原形（base form）に直したか
• 品詞：問題４で、すべての単語を使った（all）か、体言・用言だけを使った（taiyo）か、体言のみを使った（taigen）か
• STOP WORD：問題５で、STOP WORD を削除しなかった（all）か、削除した（stop）か
• ベクトル次元：問題３（200 or 300）
• train：学習に用いたデータを予測した精度（f1-macro）
• test：学習に用いなかったデータを予測した精度（f1-macro）
• diff：train - test
• all：全データを予測した精度（f1-macro）

この結果から分かること

• 問題３：全体的に 200 次元より 300 次元の方が精度が良い＝綺麗に分かれている
• 問題５：一部の品詞だけを使う場合は STOP WORD を削除した方が良いが、全部の品詞を使う場合は STOP WORD を削除すると逆に悪化する
• 問題４：だいたい、 taiyo ＞ taigen ＞ all ！
• 問題２：だいたい、base ＞ surface ！
• 一番良いのは、base_taiyo_stop_300
  • 原形に戻し、体言・用言のみを使い、STOP WORD を削除し、300 次元ベクトルを使う

正直、微妙な差すぎて上記のように言い切るのもアレだし、基本的に train をみて決めたけど all を見るとまたちょっと違う結果になったりと、色々微妙すぎる。

でも、今回の目的は実験してとりあえずでも自分の納得する方法を決めることなんだ！

だから 原形、体言・用言、STOP WORD、300 次元が最高なんや！（←必死に自分を洗脳している）

蛇足

上の評価ではマージンを１に固定しているけど、マージンを変えて計測したのが以下。単純な GridSerach しかしてないけど。

これだと、表層系のままで全部の品詞を使った方が良いのかな、とも思える。ただ、あまりにソフトなマージンだとなんだかな、ということを考えると、比較的ハードなマージンでも良い結果が出る原形で体言・用言か、もしくは体言だけでも良いのかなぁとも思う。（早速洗脳がぐらついている）

結論

日本語 Wikipedia のダンプから fastText を学習するスクリプトは以下の repository
にまとめてある。

そして今回の実験はすべてここにまとめている。

今回の実験をやってみて感じたのが「NLP ってやっぱ自由」ってこと。

決まりきった手法は無いけど、解決しなきゃいけないタスクやデータの状況、考慮したい要素などの色々なことを考えて、ベストな手法を模索していかなければならない。

文章の根本となる意味だけを捉えたい場合は体言・用言だけで良いだろうけど、例えば、時制を考えなきゃいけない場合は助動詞を加えなきゃいけないだろうし、量・大きさなどを考えたい場合は副詞を加えなきゃいけないこともあるだろう。今回は外したけど、数詞を考えなきゃいけない場合もあるだろう。

だけど、そんなこと言ってたら何も決まらないので、とりあえず better な方法を取りたいのだったら、

原形、体言・用言、STOP WORD、300 次元！

（最後に洗脳をかけ直す）

1. cosine 距離という場合はこの値を半分にして [0, 1] の範囲に収まる値を指すことがあるが、ここでは [0, 2] である上記の定義を用いる。 ↩

2. cosine 距離は spatial.distance.cdist の cosine 距離をそのまま使っているので、脚注１と同様に [0, 2] の値になる。 ↩

3. 長さ１の２つのベクトルa, b間のcosine距離は 1-ab で表せる。同様にユークリッド距離の２乗は 2-2ab になる。すると長さ１のふたつのベクトル間には「ユークリッド距離の２乗＝2*cosine距離」という関係が成り立つ。よって右下の図における青い点は $y=\sqrt{2x}$ の曲線上に乗る。またユークリッド距離における重心（算術平均）がユークリッド距離の分散を最小化するので、ユークリッド距離の重心は cosine 距離の和が最小になる点、すなわち cosine 距離の中央値（幾何学的中央値）になる。この意味で、cosine 距離の重心を取るよりも適切なのかもしれない。 ↩

4. fastText Tutorial ではベクトル次元として 100〜300 が推奨されており、学習するコーパスが大きいほど次元は増やしていくべきだとされている。そして実際にofficial に提供されている言語別の学習済みモデルは各言語の Wikipedia を 300 次元ベクトルで学習したものである。 ↩