みなさんこんにちは。PFM本部でサービス開発ディレクターをやっている伊藤です。
年の瀬ですね。私はようやく2016年がしっくり来始めたところだったのに、もうすぐ2017年かと思うと戦々恐々としています。
師走といえば忘年会ですよね。
私も色々と忘れたい事はたくさんあるので、いっぱい忘年したいと思います。
しかし、そんな時に怖いのが食費や交際費の増加ですよね。
否が応でもこの費目の出費は増えてしまいそうです。
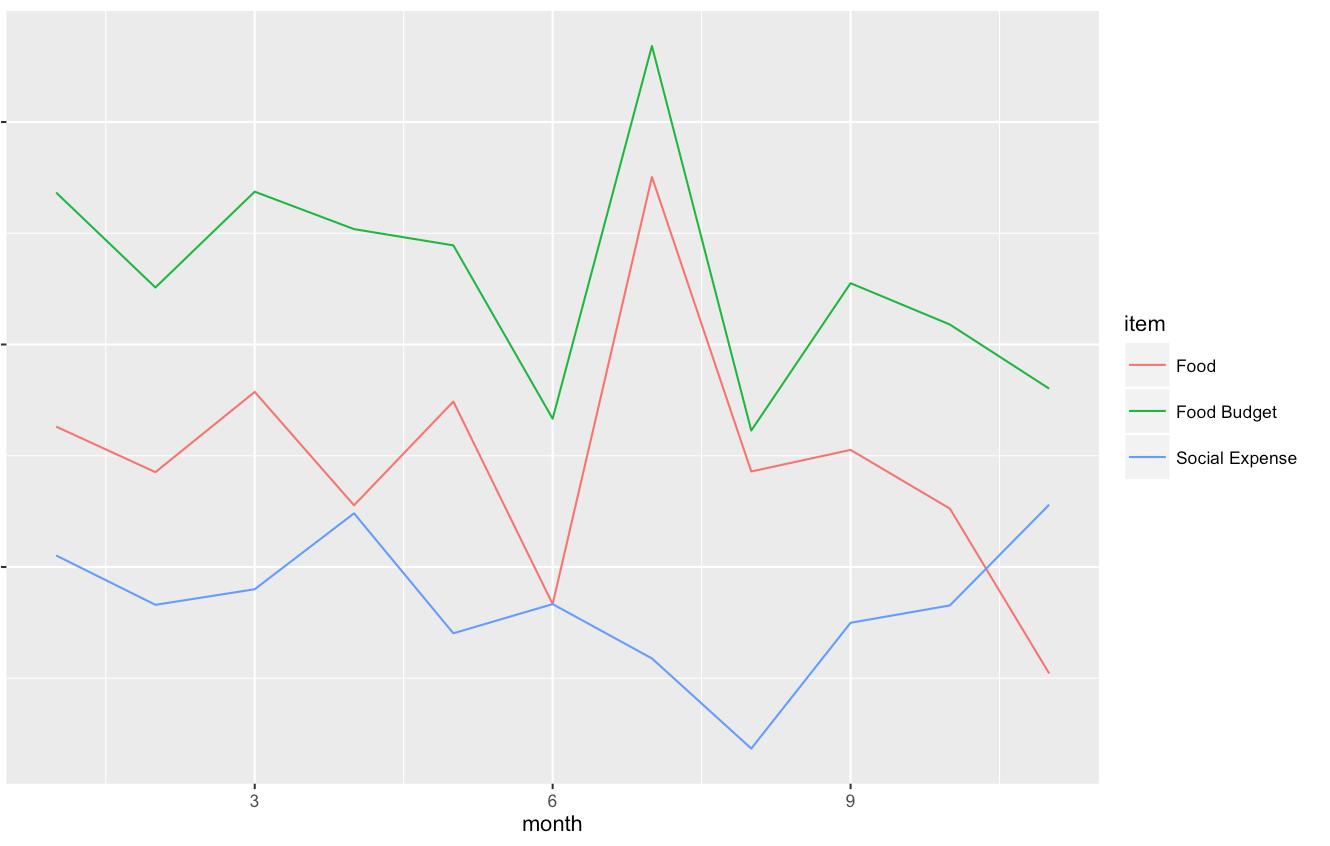
Food:食費、Social Expense:交際費、Food Budget:食費+交際費
(プライバシー保護のため具体的な金額は割愛します)
なかなか変動幅があります。
それぞれの月の項目などはマネーフォワードのアプリを紐解けばわかりますが、今回はここから先の話を考えたいです。
特に12月の出費を抑えたいという気持ちがありますので、過去の支出傾向から今月の支出を予測して、その値をベンチマークとして行動するように心がけたらどうだろうかという発想にいたります。
予測といえば、いろいろな手法がありますね。
前述のグラフを見ていただいてもわかる通り、私はR言語をよく使っていますので、R言語を使って予測をしてみましょう。
ちょうどタイミングの良いことに、先日カルマンフィルタという逐次更新アルゴリズムについて発表する機会があったので、そのアルゴリズムを使って、予測をしてみます。
まず、私の過去の支出データから状態方程式を定義します。
ある状態を構成するのは真の状態にノイズを加えたものであると定義します。
この場合のノイズはホワイトノイズとします。
今知りたいのは次の状態(t+1期)の状態ですので、t時点での状態に変動量を加えます。
変動量も基本的には正規分布に従うものとします。
初期値は私がマネーフォワードを使い始めた時点での状態とします。
定義式を記述すると下記のようになります。

これをR言語を用いて推定してみます。
カルマンフィルタを推定するパッケージはいくつかありますが、ここではKFASパッケージを用います。
最適解を探索するアルゴリズムは準ニュートン法を用いました。
予測結果の信頼区間の設定は一般的な95%信頼区間を設定しています。
R言語で記述すると下記のようになります。
library(KFAS)
mod <- SSModel(food_budget$amount~SSMtrend(1, Q = NA ), H = NA)
fit <- fitSSM(mod,numeric(2),method="BFGS")
kfs <- KFS(fit$model)
afilt <- kfs$a[-1]
Pfilt <- kfs$P[,,-1] - fit$model$Q
afiltconf <- cbind(afilt+sqrt(Pfilt)*pnorm(0.025),afilt+sqrt(Pfilt)*pnorm(0.975))
alphahatconf <- predict(fit$model,interval="confidence",level=0.95)
pre <- predict(fit$model,interval="prediction",n.ahead=10,level=0.95)
予測結果

グラフの緑の予測結果が最尤推定値となります。紫が上側95%の上限値で水色が下側95%の下限値となっています。具体的な金額は明かせませんが、予測の出力結果の95%信頼区間の下限値を予算とすれば、厳粛な予算設定とできそうです。
マネーフォワードでは上記のような手間をかけなくても予算の設定をしたり、家計診断などで適切な費目の金額を案内してくれる機能がありますので、ご安心ください。
さあ、みなさんも2017年に向けてマネーフォワードで家計管理しましょう!