$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
量子コンピュータ入門、最初の壁
最近量子コンピュータの勉強を始めた。
入門書の一番最初に量子ビットの説明が出てくる。
量子ビット自体はそんなに難しい概念ではないんだけど、突然ブロッホ球やブラケット記法なるものが導入されるのでなかなか難解な印象を受けた。
これらは物理学の分野である量子力学で出てくるものなのだけど、それらを知らない量子コンピュータ初学者は面食らってしまうのではないかと思う。
自分は量子力学を先に学んだことがあったので割とすんなり受け入れることができたが、なぜそのようなものが必要なのかを自分なりにまとめてみたいと思う。
この記事では
- 量子コンピュータとは何か
- 量子ビットとは何か
- ブロッホ球とは何なのか
- ブラケット記法とはどんなものなのか
- 考えのベースとなっている量子力学とはどんなものなのか
がざっくりわかる状態を目指す。
そもそも量子コンピュータって何?
「コンピュータはすべて1と0でできている」
というのはコンピュータに詳しくない人でも知っていると思う。
どんなに難しい計算をしている、精密なコンピュータでも、最終的には1と0の集合で表現される。
というか、あらゆるデジタル情報がそうだ。
HDDは磁石のNとSを1と0の情報として保存しているし、CDやブルーレイなどはディスクの細かいくぼみに光を当てて反射するかしないかを1と0の情報に落とし込んでいる。
メモリはコンデンサに電気が溜まっているかどうかで1,0を判断しているし、フラッシュメモリはトンネル効果によって膜を突き抜けた電子が溜まっているかいないかを判断する。
どんな高性能なコンピュータの論理演算も元を辿れば1と0である。
このようなコンピュータを量子コンピュータと区別する意味で「古典コンピュータ」と呼ぶ。
一方で、量子コンピュータでは「1と0の波の重ね合わせ」を表現することができる。
これによって計算の幅がぐんと広がる。
この性質は物理学の一分野である量子力学で発展した考え方だ。
量子力学とはざっくり言えばミクロな世界を記述するための物理学だ。
ミクロの世界だと物質の運動は波動関数と呼ばれる波の方程式で表すことができるということがわかっており、
それを情報の分野に応用したのが量子コンピュータである。
これまでコンピュータの処理速度は指数関数的に発展してきたわけだけど、それはあくまで半導体技術をはじめとするハードウェアの発達によるもので、量子コンピュータをうまく使えばより大きな計算を効率よくできるようになると期待されている。
量子ビットって何?
古典コンピュータでは1か0かといった2進数の情報をビットで表した。
量子コンピュータでは1と0の状態の波が重ね合わさった状態を表したい。
ここでベクトルを用いると便利なので導入しよう。
0,1の状態をそれぞれ $\ket{0}=(1,0)$, $\ket{1}=(0,1)$という2つの要素を持つベクトルと定義する。
適当な係数$\alpha, \beta$を用いれば重ね合わせの状態$\ket\psi$を
$$
\ket\psi = \alpha\ket{0} + \beta\ket{1}
$$
と表現できそうだ。
ちなみにこの$\ket\psi$という書き方はブラケット記法と呼ばれる記法のケットベクトルと呼ばれるものだが、後で説明するので今は単に"状態を表すベクトル"ということがわかっていれば問題ない。
状態の重ね合わせというのが一体何なのか想像できないかもしれない
量子力学の場合だと、粒子の運動が波の方程式で表されるという話は先ほどでたが、実はその波というのは複素数で記述される波であり、直接その波を観測することはできない。
粒子を観測した時点重ね合わせの状態は消えてしまうのだ。
ではその波は一体何者かというと、波の振幅の絶対値を二乗したものが粒子がそこに観測される確率を表す。
以上は量子力学における説明だが、量子コンピュータの場合も同様で、実際に観測するまでは0と1が重ね合った状態になっており、観測した時点で
確率に従って1か0に"収束する"。
逆に一度収束してしまえばそれはもう"1か0"の状態が確定してしまっているので古典ビットと変わらなくなる。
これをデコヒーレンスといい、量子コンピュータを用いるためにはこの重ね合わせの状態を維持する必要がある。
量子ビットがこのような量子性を保っていられる時間のことをコヒーレンス時間という。
SFとかでよく出てくるシュレディンガーの猫の思考実験もこのあたりに絡んだ話だ。
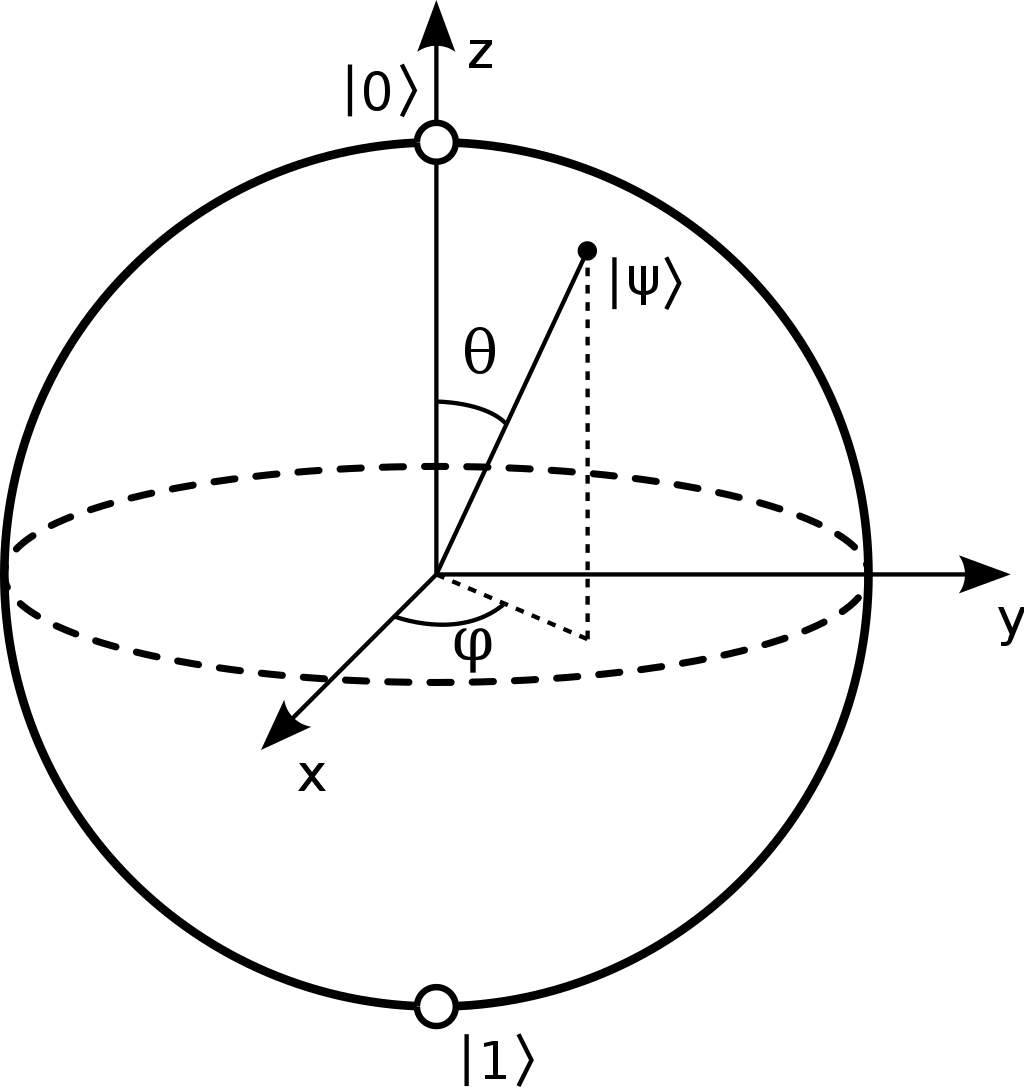
量子ビットとブロッホ球
先ほどの式に戻る。
量子力学において波の振幅の二乗が確率を表していると先ほど述べたが、今回のようなベクトルを用いた表現の場合は係数α、βの絶対値の二乗の和が1になる。
$$
|\alpha|^2 + |\beta|^2 = 1
$$
これは直感的にはすべての場合の確率の和が1になると考えればいいだろう。
例えば$\alpha = 1/\sqrt{2}$, $\beta = 1/\sqrt{2}$であれば0と1に収束する確率は等しい。
$\alpha = 4/5 = 0.8$, $\beta = 3/5 = 0.6$であれば0に収束する確率のほうがが高い。
"確率が高い"というのは何回も同じ条件で測定すれば0,1に収束する回数の比が8:6になるということである。
古典コンピュータと違って、どんなに精密に計測しても結果は確率的にしか予測できないというのが量子の世界の特徴だ。
ではこの$\alpha$, $\beta$の満たす関係式を図示するとどうなるだろうか?
上の式はぱっと見、半径1の円の方程式に似ている。
円の軌跡上のある一点を指定すれば $\alpha$, $\beta$が一意に定まりそうだ。
半径1であれば、$\alpha$, $\beta$をそれぞれcos$\theta$, sin$\theta$と置き換えれば文字を減らせそうだ。
そうすると
$$
\ket\psi = cos\theta\ket{0} + sin\theta\ket{1}
$$
となる。
だがこれは正しくない。
なぜなら$\alpha$, $\beta$ は複素数なので実数だけとは限らないからだ。
例えば$\alpha = 1/\sqrt{2}$, $\beta = i/\sqrt{2}$ のようなケースもあり得る。
この場合観測される確率は$\alpha = 1/\sqrt{2}$, $\beta = 1/\sqrt{2}$ と変わらないが、
"位相が変わっている"と表現する。
係数が複素数だと扱いが難しいので、虚数を含む部分を分離してやろう。
$$
\alpha = a e^{i\theta_1}\
\beta = b e^{i\theta_2}
$$
とでもおけば虚数の部分をexpの部分に押し付けて、a,bは実数$a^2 + b^2 = 1$の関係を満たす。
もう少しだけ詳しく説明しておくと、オイラーの公式 $e^{i\theta}=\rm{cos}\theta + i\rm{sin}\theta$ で分解すれば$e^{i\theta}$は複素平面上に書いた半径の長さ1の円上の点を表していることがわかる。
この$e^{i\theta}$で複素平面上の方向を決めて、a,bがそれぞれ長さを表していると考えれば上記の式で複素平面上の任意の点をベクトルで表現できることがわかるだろう。
ちなみに複素平面上での長さは厳密にはベクトルの"長さ"ではなく"ノルム"という表現をする。
上の式のの$a, b$はそのまま$cos\theta, sin\theta$と置き換えれるので
\begin{align}
\ket\psi &= cos\theta e^{\theta_1}\ket{0} + sin\theta e^{\theta_2}\ket{1}\\
&= e^{\theta_1}(cos\theta \ket{0} + sin\theta e^{(\theta_2-{\theta_1})}\ket{1})\\
&= e^{\Phi}(cos\theta \ket{0} + sin\theta e^{\phi}\ket{1})
\end{align}
と変形できる。
最後の変形で$\theta_1, \theta_2 - \theta_1$をそれぞれ$\Phi,\phi$と置いた。
ここで$e^{\Phi}$の部分は全体の位相(グローバル位相)なのでいったん無視すると、
残りの部分は$\theta, \phi$で指定できる球面上の一点を表す。
この球面のことをブロッホ球という。
球面において$\theta$は0-$\pi$を動くが、全体の正負は$e^{\Phi}$の部分に押し込めるため、cos$\theta$の$\theta$の範囲
は0から$\pi /2$まで動けば十分である。
そのへんを考慮して上の式で$\theta$ -> $\theta/2$とすれば最終的に
$$
\ket\psi = e^{i\Phi}\left(cos\frac{\theta}{2}\ket{0} + sin\frac{\theta}{2}e^{i\phi}\ket{1}\right)
$$
いろいろと難しいことを言ったけど、
"$\ket\psi$の状態は$\alpha, \beta$を指定することで決まり、球面上のある一点に対応しますよ"
ということを言っているだけなので、ブロッホ球自体がそこまで深淵な話でもない。
ちなみにこのあたりの計算は物理学だと"スピン"と呼ばれる物理量の計算で出てくる。
参考:https://eman-physics.net/quantum/bloch_sphere.html
ブラケット記法のあれこれ
$\ket{0}=(1,0)$, $\ket{1}=(0,1)$はそれぞれ2つの要素を持つ列ベクトルであるため、例えば(2×2)の行列をかけて別のベクトルに変換することができる。
そもそも内積やノルム(ベクトルの長さ)の計算をするにはどうしたらいいだろうか?
例えば$\ket{0}$の自分自身との内積(=ベクトルの長さの二乗)を計算するには$\ket{0}$を転置して列ベクトルにした後に内積を取ればよさそうだ。
\left(\begin{array}{cc} 1&0\end{array}\right)\left(\begin{array}{cc} 1 \\ 0 \end{array}\right) = 1^2 + 0^2 = 1
これが複素数の場合はどうだろう。
例えば(i,0)というベクトルの長さ(今後ノルムと呼ぶ)を計算したい場合を考える。
結論を言えば、転置した上で複素共役をとったものをかければ計算できる
\left(\begin{array}{cc} -i&0\end{array}\right)\left(\begin{array}{cc} i \\ 0 \end{array}\right) = -i^2 + 0^2 = 1
複素共役を取ることで複素数の実数部分だけを取り出すことができるのだ。
内積の場合も同様に計算できる。
上の$\ket{0}$, $\ket{1}$のベクトルは内積を取れば0になる(直交している)ことがわかるだろう。
このようにベクトルのノルムが1で軸が直行しているような軸を正規直交基底という風に呼ぶ。
このように複素数の行列、ベクトルの計算においては"転置+複素共役をとった上で内積をとる"という計算をする頻度が多い。
この転置+複素共役をとることをエルミート共役と言ったりする。
このエルミート共役を†という記号で定義し、さらに以下のような表記を定義する。
(\ket\phi)\dagger = \bra\phi
$\ket{0}$の表記をケットベクトルと呼び、$\bra{0}$の表記をブラベクトルと呼ぶ。
ブラケットというのはもともと"カギかっこ"という意味で、「ブラ」「ケット」というのは一つの単語を無理やり分解した言葉遊びのようなものだ。
このブラベクトルとケットベクトルを使えば、上の方でやった内積やノルムの計算は以下のように(文字通り"ブラケット"に合体させて)簡単に表記できる。
\braket00 = 1 \\
\braket11 = 1
同様に内積は
\braket01 = 0 \\
\braket10 = 0
のように書ける。
$\ket\phi$のノルムも計算してみよう。
\ket\psi = \alpha\ket{0} + \beta\ket{1} = \left(\begin{array}{cc} \alpha \\ \beta \end{array}\right) \\
\bra\psi = (\ket\psi)\dagger = \left(\begin{array}{cc} \alpha^* & \beta^* \end{array}\right) \\
\braket\psi\psi = |\alpha|^2 + |\beta|^2 = 1
といった具合に計算できる。
これは物理学者のディラックが考えた記法である。
量子コンピュータの入門書の最初の方にいきなりこいつが出てくると混乱すかもしれないが、
単に行列、ベクトルの計算を完結に行うための表記だと割り切れば良い。
基底の選び方
これまでベクトルを表現するのに$\ket{0}, \ket{1}$を採用してきたが、このようなベクトルを表現するために使う軸を基底という。
基底には互いに直交して大きさが1の軸を選ぶ必要がある。これを正規直交基底という。
先ほどの内積の計算でこれらは示せた。
今までは$\ket{0}=(1,0)$, $\ket{1}=(0,1)$というように2つの軸を選んで係数α、βを決定することで$\ket\psi$の状態を決定したが、$\ket\psi$をベクトルで表現することが目的であれば別の軸を選んでも問題ない。
ただ、どんな軸でも言い訳ではなく、正規直交基底という条件を満たす必要がある。
例として以下はアダマール基底と呼ばれ、正規直交基底の条件を満たす。
\ket+ = \frac{1}{\sqrt{2}}(\ket0 + \ket1) \\
\ket- = \frac{1}{\sqrt{2}}(\ket0 - i\ket1)
ある基底から別の基底への変換は行列をかけてあげることで可能である。
例えば2*2の要素を持つ行列Uを作用させて
\ket{0'} = U \ket0 \\
\ket{1'} = U \ket1
という風に変換が可能だ。
ここで注意しなければならないのが、変換前の基底が正規直交基底であったとしても変換後の基底のノルムが1である保証はないということだ。
もし変換後も正規直交基底であればノルム
\braket{0'}{0'} = \bra0 {U\dagger}U \ket0 \\
が1にならなければならない。$\braket00 = 1$ だったことを思い出せば、行列Uは
UU\dagger = {U\dagger}U = 1
を満たしていればいい。
言い換えれば
U\dagger = U^{-1}
ということだ。このような行列をユニタリ行列という。
量子力学との関係性
最初にベクトルの和で$\ket\psi$を表現したとき、量子力学においては"波の重ね合わせ"で表現できると言った。
だが、式だけ見るとただのベクトルの和なのでどこが波なのかよくわからないかもしれない。
実は量子力学においてこのブラケットを用いた表記は少々抽象化した書き方であり、シュレディンガーという物理学者の流儀だと波動関数$\Phi$はcosやsinを用いた複素数の波の形で表現できる。
かなり乱暴な言い方をすれば、量子力学とは粒子の運動に複素数の波の方程式(=シュレディンガー方程式)を当てはめて解く学問である。
一方でフーリエ級数展開という手法を用いればあらゆる周期関数はsin, cosの足し合わせで表現できる。
f(x) = \Sigma_n{c_n}e^{i\frac{2\pi}{L}nx}
上の式は周期Lの場合だが、あらゆる形の波は上のような形式で表現できる。
$e^{i\frac{2\pi}{L}nx}$の部分がよくわからないかもしれないが、オイラーの公式 $e^{i\theta}=\rm{sin}\theta + i\rm{sin}\theta$ で分解すればsinとcosの重ね合わせで表現されていることがわかる。
さらに言えば、nで足し合わせる時のcos$\frac{2\pi}{L}x$, cos$\frac{2\pi}{L}2x$, cos$\frac{2\pi}{L}3x$...の部分は全て直交する。
つまり、$e^{i\frac{2\pi}{L}nx}$の部分はnで足し合わせたときの正規直交基底にあたり、波の形を決める要素は$c_n$である、と言えそうだ。
そこで$c_n$をベクトルで表現して、波動関数も物理量も全てベクトルや行列で定義したほうが綺麗に書けるよね、というのが量子力学での考え方だ。
なので、ブラケット記法で表記されたベクトルだけみてもどこが波の重ね合わせなのかわからないかもしないが、基底となっているcos, sinが量子力学においては波を表しているという風に(自分は)理解している。
まとめ
- 量子コンピュータの入門書でいきなり導入されるブロッホ球やブラケット記法がどのようなものなのかまとめた
- ブロッホ球上の一点はベクトル$\ket\psi$の状態を表す
- ブラケット記法を用いると内積などの関係式がすっきり書けるので導入している
- これらの考え方のほとんどは量子力学から輸入している
物理出身のエンジニアなのでかなり物理寄りの説明になってしまった。
間違いや補足などがあれば教えてもらえると喜びます。