はじめに
今やビットコインや仮想通貨という言葉を知らない人はいないと思います。
数年前に仮想通貨ブームなるものがおきて「億り人」なる人たちが出てきたりしましたのも記憶に新しいですね。
多くの芸能人も手を出していて、TVでCMも頻繁に流れていました。
僕は当時まったく興味がなかったのですが、最近になって仮想通貨や、そのベースのテクノロジーであるブロックチェーンについて興味が湧いてきました。
歴史上、最初に仮想通貨として登場したのがビットコインです。
ビットコインの誕生について調べるてみると、一人の人物の名前が浮かび上がります。
それがサトシナカモトです。
2009年、このサトシナカモトによるわずか9ページの論文によって初めてビットコインやブロックチェーンの概念が生まれたのでした。
日本人のような名前ですが、実際の国籍はおろか、一人なのか複数人なのかすらわかっていないようです。
今現在も正体は不明ということです。
そんな歴史的な論文がこちらです。
"Bitcoin: A Peer-to-Peer Electronic Cash System"
https://bitcoin.org/bitcoin.pdf
今更ですがこの論文を読んで感銘を受けたので、ブロックチェーンの成り立ちについて自分なりにまとめてみようかと思います。
最後に原著論文に書いてある数式をPythonで可視化して検証してみます。
わかりやすくするために、論文には書かれていない説明もちょこちょこ挟んでます。
なぜブロックチェーンが必要か?
普段はあまり意識しないかもしれませんが、僕たちが誰かと金銭を伴う取引をするときは必ず信用できる第三者の存在があります。
例えば誰かにお金を送金する時は「銀行」や「クレジットカード会社」などです。
なぜこれらが必要なのでしょうか?
例えば家族などの信頼できる人にお金を払うようなケースであれば直接会って手渡しするようなことも可能かもしれません。
でも多くの場合、相手が100%信頼できる相手とは限りません。
後から返してもらう約束で送金しても、実は相手が悪い人で持ち逃げされてしまう可能性があります。
そのため「銀行」や「カード会社」などの誰もが信頼できる第三者に取引の仲介をしてもらうのです。
メルカリやヤフオクで商品を売買する場合も仲介してくれる会社が存在するから安心して取引できるわけです。
そもそもただの紙切れにすぎない日本円をみんなが疑わずに使っているのも日本という国やその国の銀行に信用があるからです。
これは実はいいことだけではありません。
例えばカード会社などのケースだと、第三者が仲介することで仲介料が取られますね。
また、日本円の例だと「どれくらいお金を刷るか?」といった金融政策などはすべて国が決定します。
僕たち日本国民に一切の決定権はないので政府の政策に振り回されることになります。
また、国が完全に信用できるとも限りません。
例えばトルコという国の通貨(トルコリラ)は周囲で戦争、紛争が頻繁におきているためかなりのリスクがあります。
ギリシャは借りたお金が返せなくなって財政破綻したことがありますし、アルゼンチンも外国債で同様に破綻しています。
このように国の信用というのも常に揺らいでおり、いつ何が起こるかわからないのです。
これをテクノロジーの力で解決しようとしたのがブロックチェーンです。
要はお金を安全に送る仕組みさえ作れば信用できる第三者なんていらなくなるというかなり革命的な発想なのです。
第三者のいない直接的なやりとりをPeer to Peer (P2P)と読んだりします。
論文のタイトルになってる"Peer-to-Peer Electronic Cash System"というのはお金を送る人と受け取る人が直接やりとりできるシステムということです。
ブロックチェーンの仕組み
誰かから誰かに送金する際、ブロックチェーンにおいては電子署名の仕組みを使います。
電子署名というのは簡単に言えば公開鍵と秘密鍵という二つの鍵を使って改ざんが不可能にする仕組みです。
公開鍵と秘密鍵は必ずセットで生成されます。
秘密鍵で記録(厳密にはそこから生成したHash値)を暗号化し、公開鍵で復号します。
秘密鍵は自分だけで大事に保管しておきますが、公開鍵は広く公開してしまって大丈夫です。
重要なのが、秘密鍵で生成した暗号はセットの公開鍵でしか復号できないということです。
なので、暗号化された情報を公開鍵を使って復号することができれば、確かに送り主の送ってきたものに間違いないということがわかるわけです。
これが印鑑や署名の仕組みと似ているため電子署名と呼びます。
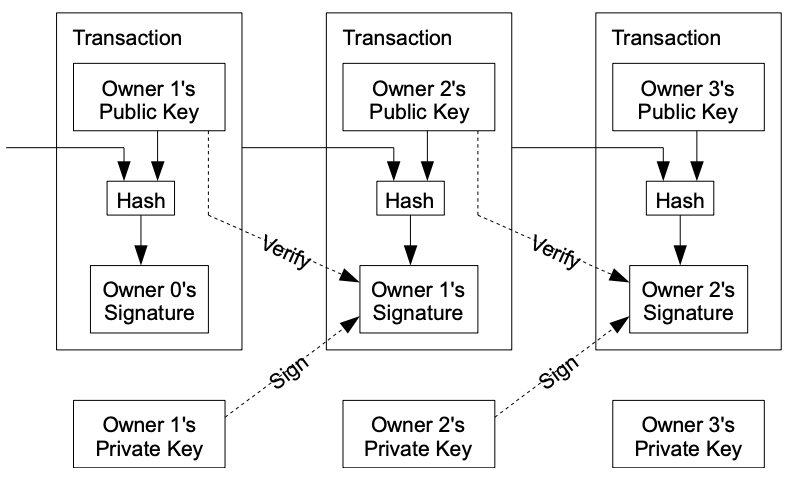
下の図で具体的に考えてみます。
Owner1からOwner2, Owner2からOwner3へと、取引一つひとつが"Transaction"として繋がっています。
ここでいる取引とは送金をイメージしてもらえれば大丈夫だと思います。
送信者(Owner1)は秘密鍵(Private key)を使ってHash値と呼ばれる値を暗号化し、公開鍵(Public key)と一緒に受信者(Owner2)に送ります。
受信者はOwner1からもらった公開鍵を使ってHash値を復号し、送られてきたデータから計算されるHash値と同じかどうかを確かめます。
もしHash値が一致すれば改ざんされていないということがわかります。
もし途中でデータが改ざんされてしまうと、そこから計算されるHash値も変わってしまうからです。
「本当は1万円しか送ってないけど改ざんして100万円くらい送ったことにしたろ!」
みたいのを防げるわけですね。
ちなみにこの電子署名の仕組み自体は特に新しい技術ではなく、昔からよく使われてきました。
また、論文によると公開鍵の公開範囲を絞ることでプライバシーを守ることも可能だと書いてあります。
わかりやすくするためにもう一つだけ別の例を考えてみます。
Amazonで机を買ったとします。
無事家に机が届いて組み立てるときに、説明書にこんなことが書いてあったとします。
「この机の部品としてネジがn本、板がm本入っています」
当たり前ですが、実際に届いた机の部品である板やネジの本数は説明書と一致しているはずですよね。
もし配送中に悪い人間がこっそりネジを何本か抜き取っていれば、説明書に記載されたネジの数と実際に数えたネジが食い違うはずです。
Timestampの仕組み
上でみた電子署名の仕組みは改ざんは不可能になりますが、実は二重支払いの問題を解決できません。
通常の送金であれば信用できる第三者が全部の記録を監視してくれているので払い戻しなどをしてくれます。
「◯月✖︎日と◯月△日に確かに支払いの記録がありますね。二重支払いになってるので払い戻します」
といった感じです。
ただ、最初にも言った通りブロックチェーンでは信頼できる第三者が必要ない仕組みを目指します。
そこで、取引ごとにtimestamp(要は取引があった時間)を記録し、その時間に確かにその取引があったことを記録します。
さらにその記録が現在でも改ざんされていないことを保証します。
このtimestampを記録するサーバをtimestamp serverといいます。
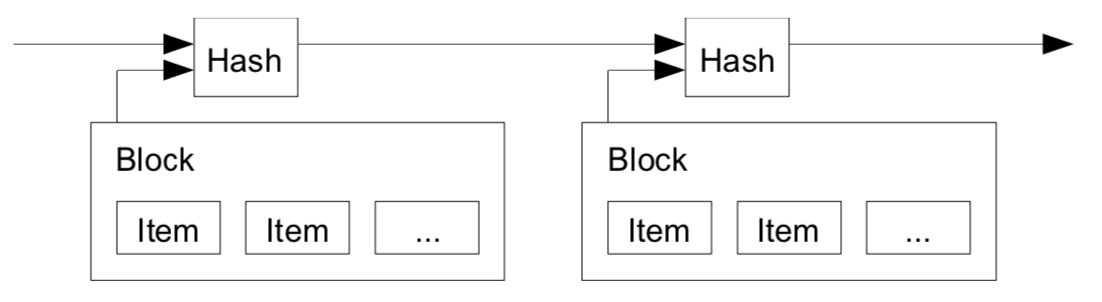
このtimestampは取引のHashと共に記録され、チェーンのように連なっていきます。
これで「いつ」「どんな」取引があったかがわかるようになります。
さらに、ブロック一つひとつがチェーンのように連なっていることで、後から記録を改ざんするのを防ぐこともできます。
ひとつひとつのブロックはその前の取引のHashも参照しているため、一箇所を改ざんすると前後のブロックと整合性がとれなくなってしまうためです。
そのため、もし一箇所を改ざんしようと思ったら連なるすべてのblockを改ざんしなければなりません。
これらのhashとtimestampは広く公開されるため、もし不正があれば誰かがその矛盾に気づくことになります。
timetampについては以下のページが非常にわかりやすかったです。
https://www.ogis-ri.co.jp/otc/hiroba/technical/bitcoinpaper/part4.html
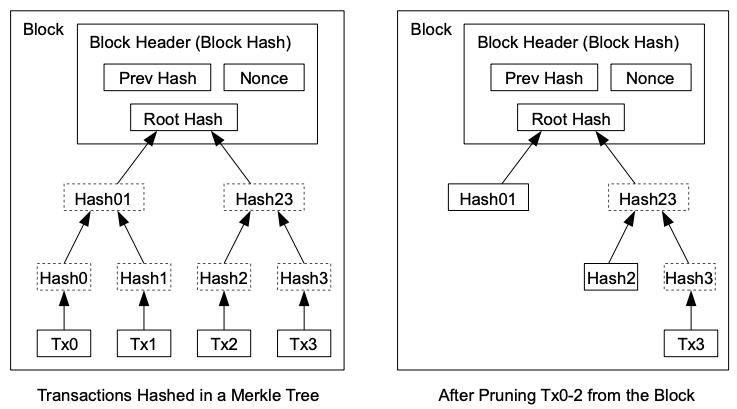
さらに効率よくtimestampとHashを記録するために、この論文ではMarkle tree(要は二分木)を使った方法が紹介されています。
例えばTx0, Tx1, Tx2, Tx3と4つの取引があった時、一つ一つのHashとtimestampをすべて記録するのではなく、4つまとめて記録する方法です。
このときもともとの4つの取引からはHash0, Hash1, Hash2, Hash3が生成されます。
ここでHash0とHash1からHash01, Hash2とHash3からHash23、さらにHash01とHash23からRoot Hashを生成することで4つのHashをひとつにまとめてしまうのです。
4つにまとめてしまうことでこの4つの取引の前後関係はわからなくなりますが、Blockごとの前後関係はすべて記録されているため、計算リソースを節約できます。
Proof of work
さて、timestamp serverが取引時間と取引の記録であるHashをセットにして記録することで安全な取引が実現できることがわかりました。
では誰がtimestampを発行するのでしょう?
ブロックチェーンの目指すところは「信用できる第三者」がいない世界です。
特定の誰かに依存しないようなしくみが必要です。
ここで採用された仕組みがProof of work(PoW)です。
簡単に言うと、みんなでCPUパワーをつかってガンガンHash値を計算し、最初に正解のHash値を見つけた人がブロックに書き込むことができるという仕組みです。
最初にHash値を見つけた人には報酬としてBitcoinをもらうことがきます。
これは金脈をガンガン掘り当てて金を採掘する行為に似ているため「マイニング」と呼ばれます。
ではなぜPoWが必要なのでしょうか?
例として多数決のように「IPアドレス一つにつき1票投票できる」ような仕組みを考えてみましょう。
一見よさそうに見えますが、記録の改ざんを企む人が大量のIPをかき集めてしまえばブロックの書き換えができてしまいます。
ブロックチェーンは参加者がみんなでブロックを書き込んでいく仕組みなので、全体の過半数を書き換える力を誰かが手に入れてしまった瞬間にこの仕組みは破綻します。
計算
では、このブロックチェーンが果たしてどれくらい安全なのか、計算してみましょう。
ここで攻撃者(悪い奴)がいたとします。
ブロックチェーンは仕組み上扱ったことのないコインを無から生み出すことはできません。
攻撃者ができることは自分の取引記録を書き換えることだけです。
もし攻撃者があるブロックを書き換えたとしても、チェーンで繋がれた次のブロックでハッシュ値が一致しないのがわかると不正がバレてしまいます。
なので、攻撃者が不正をするには正しいnodeから繋がっていくチェーンよりも早いスピードで不正なチェーンを生成しなければなりません。
nodeが分岐している場合は長いチェーンが採用されるため、不正を行うためには正しいチェーンよりも長いチェーンを作る必要があります。
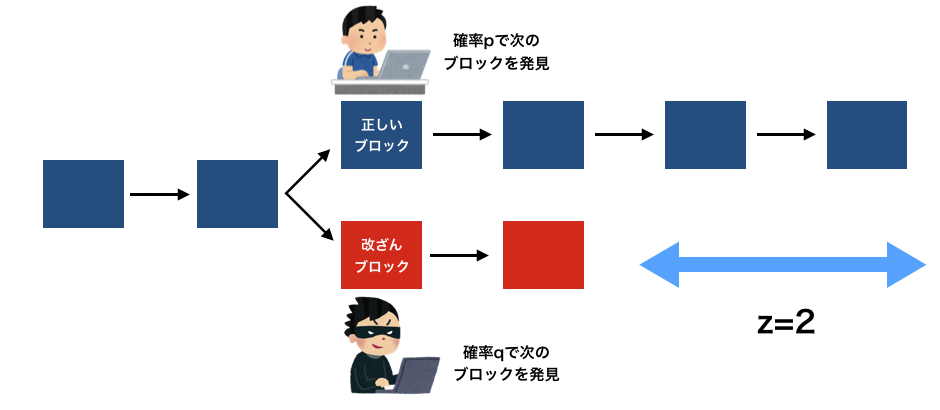
この設定を図にすると以下のような感じでしょうか。
- p: 正しいnodeが次のブロックを見つけられる確率
- q: 攻撃者が次のブロックを見つける確率
- z: 攻撃者が追いつくために必要なブロック数
とすると、攻撃者が追いつく確率qzは以下のように表すことができます。
q_{z}=\left\{\begin{array}{cc}
1 & \text { if } p \leq q \\
(q / p)^{z} & \text { if } p>q
\end{array}\right\}
ここで、攻撃者がブロックを見つけられる確率はその他大勢による正しいブロックが見つけられる確率に比べると低いはずです。
なので、p>qと仮定します。
具体的に考えてみましょう。
例えば攻撃者が次のブロックを見つける確率が1%、正しいnodeが次のブロックを見つける確率が10%としましょう。
攻撃者が追いつくのに必要なブロックが1(z=1)だとすると、
q_{z}=\begin{array}{cc}
(0.01 / 0.1)^{1} = 0.1&
\end{array}
となります。ここで出した数値はあくまで例なので実際の数字とは全然関係がないです。
zが大きくなるほど攻撃者が追いつくのは指数関数的に難しくなるのが感覚的にわかると思います。
この設定について原著論文では"Binomial Random Walk"(二項ランダムウォーク)と呼んでいます。
一定確率でzの距離はz+1になり、また一定の確率でz-1に縮まるため、二方向へのランダムな動きをするためです。
また、この問題をGambler's Ruin problem (ギャンブラーの破産問題)のアナロジーだとも言っています。
例えば、AさんとBさんが賭け事をしているとします。
コインで表が出ればAさん->Bさんに10万円、裏が出ればBさん->Aさんに10万、といったような設定を考えたときにAさんBさんそれぞれが破産する確率を考えるのです。
例えばAさんの資金が10万円しかなければ、最初に表が出た時点でAさんは破産してしまいますね。
今回のケースだと、"破産"は存在しません。
無限に試行を繰り返して最終的に攻撃者がzの差を追いつく確率を考えれば良いのです。
そのため、このケースだと無限の資産を持つギャンブラーの破産問題に置き換えて考えられます。
この問題についてはググるといっぱい説明が出てきます。
ここで重要なのはz=1くらいだとラッキーパンチで攻撃者が追いつく可能性がありますが、時間が経てば経つほど追いつくのが難しくなるということです。
では、どれくらいの時間までば安心できるでしょうか?
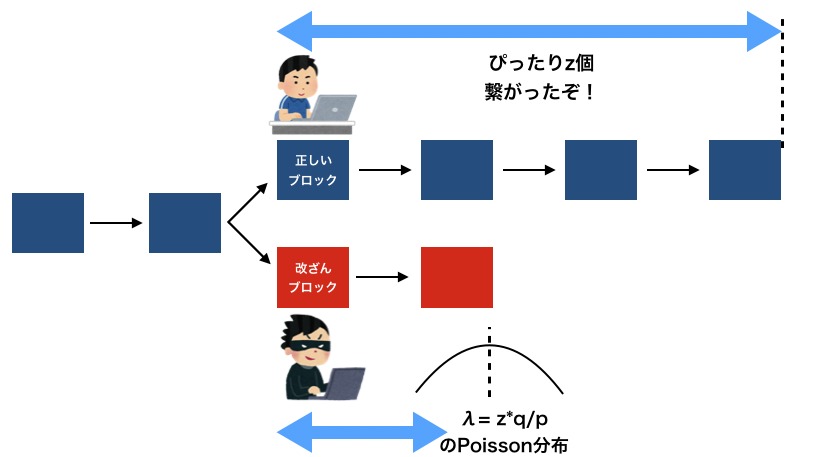
取引が終わってz個の正しいブロックを繋がった場合を考えます。
この時攻撃者が改ざんを行なっているとして、正確に何個のブロックを改ざんできたかは受け手からはわかりません。
ですが、改ざんが成功する確率をqとすればだいたい
\lambda = z\frac{q}{p}
くらいの進捗でブロックを繋げられていることがわかります。
例えば攻撃者がブロックを発見できる確率が正しいブロックの半分の確率だった場合、だいたいz/2個のブロックを見つけられていることになります。
攻撃者が正確に何個のブロックを生成できているかは受けてからはわからないので、確率分布を考えます。
生成できているかどうかは二択なので二項分布を考えればよさそうですが、ここではポアソン分布を考えます。
なぜポアソン分布なのでしょうか?
二項分布において試行回数->∞、確率->0に極限をとったものがポアソン分布です。
ブロックチェーンの場合だと、攻撃者は低い確率で多くの回数トライしていると考えればこの仮定は正しそうですね。
なので、期待値λを上で定義した上でのポアソン分布を考えてみると、以下のように書けます。
P(k) = \frac{\lambda^{k} e^{-\lambda}}{k !} \begin{array}{cc}
\end{array}
kは横軸でλはパラメータと考えるとイメージしやすいです。
これが攻撃者がいくつのブロックを生成できているかの確率分布になります。
イメージ的にはこんな感じですかね。
この状態で攻撃者が追いつく確率を計算してみましょう。
攻撃者の現在地をkとした場合にz-kを追いつけば良いわけなので、確率分布のすべてのkについて和をとれば良いです。
\sum_{k=0}^{\infty} \frac{\lambda^{k} e^{-\lambda}}{k !} \cdot\left\{\begin{array}{cc}
(q / p)^{(z-k)} & \text { if } k \leq z \\
1 & \text { if } k>z
\end{array}\right\}
ここで、確率分布なのでk>z、つまり正しいブロックがz個繋がった時に攻撃者がそれ以上のブロックの生成に成功している可能性も0じゃないので場合分けされてます。
プログラムで計算する場合は無限大が出てくるのは都合が悪いので、変形します。
上の式は以下のように書き換えられます。
\sum_{k=0}^{z} \frac{\lambda^{k} e^{-\lambda}}{k !}
(q / p)^{(z-k)} + \sum_{k=z}^{\infty}\frac{\lambda^{k} e^{-\lambda}}{k !} \\
= \sum_{k=0}^{z} \frac{\lambda^{k} e^{-\lambda}}{k !}
(q / p)^{(z-k)} + 1 - \sum_{k=0}^{z}\frac{\lambda^{k} e^{-\lambda}}{k !} \\
=1-\sum_{k=0}^{z} \frac{\lambda^{k} e^{-\lambda}}{k !}\left(1-(q / p)^{(z-k)}\right)
可視化
Pythonとmatplotlib可視化してみます。
なお論文ではC言語を使って同じような計算をしています。
import math
import numpy as np
import matplotlib.pyplot as plt
def AttackerSuccessProbability(q, z):
p = 1.0 - q;
lam = z * (q / p);
sum_k = 1.0;
for k in range(z+1):
poisson = math.exp(-lam);
for i in range(1, k+1):
poisson *= lam / i;
sum_k -= poisson * (1 - (q/p) ** (z-k) )
return sum_k
q1 = 0.1
q2 = 0.3
Nz = 10
# q=0.1
p_list1 = []
p_list2 = []
z_list = []
for z in range(Nz):
P1 = AttackerSuccessProbability(q1, z)
P2 = AttackerSuccessProbability(q2, z)
z_list.append(z)
p_list1.append(P1)
p_list2.append(P2)
plt.plot(z_list, p_list1,
color='blue', marker='o',
markersize=5, label='q=0.1')
plt.plot(z_list, p_list2,
color='red', marker='o',
markersize=5, label='q=0.3')
plt.grid()
plt.xlabel('z')
plt.ylabel('P')
plt.legend(loc='upper right')
plt.ylim([0., 1.0])
plt.tight_layout()
plt.show()
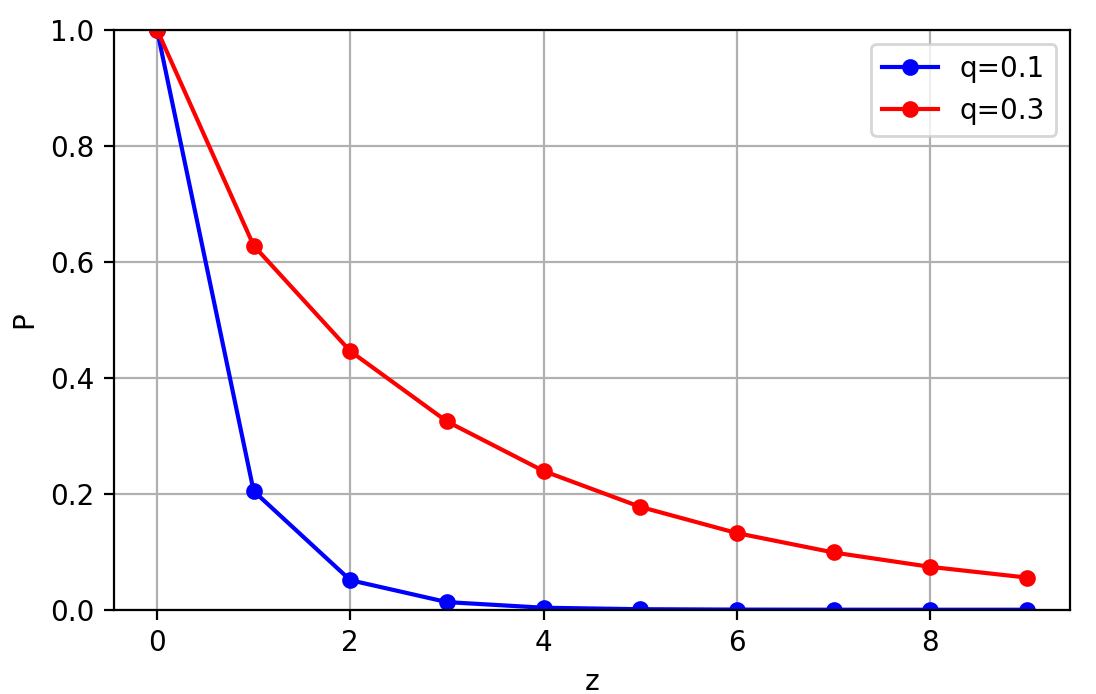
ここではq=0.1, q=0.3の2パターンについて可視化しています。
正常なnodeからブロックを計算する数が多ければ多いほど不正は難しくなることがわかります。
また、zが多ければ多いほど不正が難しくなることもわかります。
まとめ
- ブロックチェーンを使えば「信頼できる第三者」を必要としないP2Pの送金の仕組みを作ることができる
- PoWの仕組みを用いることで、記録の改ざんを難しくすることができる
備考
- 論文を読み終わってから論文のタイトルにもなってるビットコインという単語が論文中に一切出てこないことに気づいた
- タイトルにだけ入れたのはどのような真意なのだろう?
- ちなみにPoWについては世界中の人がみんなビットコインを使った取引をし始めると電気代がやばいことになるのでPoW脱却しなきゃみたいな動きもあるみたいです
- 代わりとして考案されてるのがProof of Stake (PoS)と呼ばれるもので、コインの保有量が多いほどブロックが生成しやすくなる仕組みです(地球に優しくていいね!)