Go to Qiita Advent Calendar 2024 Top
LoginSignup
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@tetsuro731(テッツォ)

A/BテストでCUPEDを使って分散を小さくする

Last updated at Posted at 2024-11-15

はじめに

A/BテストやRCTと呼ばれるランダム化実験はウェブアプリをはじめさまざまなサービスで利用されている。
ここでは「より少ないデータで、より正確に効果を測るための手法」であるCUPEDについて紹介する。
CUPEDは"Covariate Using Pre-Experiment Data"の略で、簡単に言えば「実験前のデータを使ってA/Bテストの精度を上げる方法」だ。

A/Bテストのおさらい

A/Bテストは、ウェブやアプリの改善に欠かせない手法だ。
具体的には、ユーザーをランダムに2つのグループに分け、片方には従来のバージョン（コントロール群=Control group）、もう片方には新しいバージョン（処置群=Treatment group）を見せて、どちらが効果的かを検証する。

A/Bテスト最大の利点は"ランダム化"にある。

比較する2つの集団にバイアスがあれば平等な比較はできない。
あるいは、同じユーザーにおける比較でも施策の"前後"で比較してしまうと季節性など
さまざまな影響を受けて正確な測定が難しくなる。
（Conterfactual ModelやDIDなど高度な分析や余分な仮定が必要になってしまう）

その点A/Bテストは同じ時間軸でバイアスのない母集団の比較が可能だ。
つまり、CTRやCVRなどの見たい評価指標を直接的に比較することが可能になる。

「TreatmentのCVRは7%でControlは5%だった。Treatmentのほうが精度が高いから本番導入しよう！」

みたいな意思決定ができるということだ。
もちろん有意差を正確に測定しようと思ったらt検定を始めとして検定が必要になるが、余計な仮定を減らして問題を単純化できるといったメリットがある。
従って、もし可能であればできるだけRCTを行うのが推奨される。

CUPEDって何？

ではA/Bテストにおける最大の関心ごとは何だろうか？
いくつか重要な要素はあるが、その一つが
「いかにして統計的なばらつき（分散）を小さくするか」

ということだ。
例えば1%の有意差を測定したいのに統計誤差が3%あれば当然見ることはできない。
仮に実測値として差があってもそれが"誤差の範囲"とみなされてしまうからだ。
分散を減らす方法としては

  • サンプル数を増やす
  • 実験期間を長くする

などがあるが、いずれも実験を設計する段階である程度見積もる必要がある。

CUPEDは簡単に言えば実験後、分析の段階で「実験前のデータ」を使い、分散を減らすことでA/Bテストの精度を上げる手法だ。

数式を使った説明

もう少し詳しくみてみよう。
A/Bテスト結果の単純な比較だと、使うデータは"テスト期間中のもの"に限られる。
例えばテスト期間が2週間であれば、その間の評価指標（CTRやCVR、売上げなど）が対象となる。

だが、CUPEDでは「実験前のデータも使えないだろうか？」と考える。
例えばユーザー単位で指標を見ている場合、実験前の期間のCVRや売上げもある程度実験中の値と相関してそうに思える。

ここで、実験中の見たい指標Yに対して実験前の指標をXとし、以下のように

$$
Y_{\text{CUPED}} = Y - \theta X
$$

を定義してみる。ここ$\theta$はパラメータである。
分散は以下のように書ける。

\text{Var}(Y_{\text{CUPED}}) = \text{Var}(Y) + \theta^2 \text{Var}(X) - 2\theta \, \text{Cov}(X, Y)

A/Bの単純な比較だとYの分散が重要になるが、$Y_{CUPED}$をそれより小さくしたい。
そのためには$\theta$にどのよう値を採用すればいいだろうか？
$\theta$で微分して0になるような値を求めてあげればよさそうだ。
つまり、

2\theta \text{Var}(X) - 2\, \text{Cov}(X, Y) = 0 \\

\begin{aligned}
\theta = \frac{\text{Cov}(X, Y)}{\text{Var}(X)}
\end{aligned}

となる。
これを先ほどの式に代入してみよう。

\begin{aligned}

\text{Var}(Y_{\text{CUPED}}) &= \text{Var}(Y) \left(1 + \frac{\theta^2 \text{Var}(X)}{\text{Var}(Y)} - 2\theta \, \frac{\text{Cov}(X, Y)}{\text{Var}(Y)}\right)\\
&= \text{Var}(Y) (1 + \rho^{2} - 2\rho^{2}) \\
&= \text{Var}(Y) (1 - \rho^{2})
\end{aligned}

とかなりすっきりとした結果になる。
ここで$\rho=\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}$はPearsonの相関係数である。

ここからわかるのは、
「実験前と実験中の指標の相関が大きいほど分散を小さくできる」
ということだ。
これは直観とも合う。
もし実験前のデータが完全に無相関なら実験で得られた指標の測定には役に立たなそうだが、ある程度相関があれば、追加の有益な情報として使えるからだ。

どんな時に使うべき？

さて、これでおおよそのアイディアは分かったがどのようなときに使えばいいのだろうか？
これまでの議論を踏まえると

  • 使える場合
    • 実験前のデータがある程度相関してそう
    • 限られたサンプルサイズでできるだけ分散を減らしたい場合
  • 使わなくてもいい場合
    • 事前にA/Bテストがしっかりデザインされており、単純比較でも十分有意差の検定ができる場合
    • 実験前のデータがない or ほぼ相関してない場合

とまとめることができそうだ。

簡単なシミュレーション

さて、数式だけだと味気ないので最後にPythonで簡単なシミュレーションもしてみよう。
CUPEDを使わない場合と、使った場合で標準誤差がどのくらい変わるか見てみる。
なお、今回はPythonだが統計分析だとRが用いられることも多い。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# Data generation
np.random.seed(42)
n = 4000  # Sample size

# Pre-experiment data (pre-metric)
pre_metric = np.random.normal(50, 10, n)

# Post-experiment target (adding a small effect)
treatment_effect = 1.5  # Effect size
post_metric_control = pre_metric + np.random.normal(0, 5, n)  # Control group
post_metric_treatment = pre_metric + treatment_effect + np.random.normal(0, 5, n)  # Treatment group

# A/B test variance comparison (before applying CUPED)
ab_diff = post_metric_treatment.mean() - post_metric_control.mean()
ab_std = np.sqrt(np.var(post_metric_treatment) / n + np.var(post_metric_control) / n)

# Applying CUPED
# Subtracting predicted values based on the covariate
X = pre_metric.reshape(-1, 1)
y_control = post_metric_control
y_treatment = post_metric_treatment

model_control = LinearRegression().fit(X, y_control)
model_treatment = LinearRegression().fit(X, y_treatment)

post_metric_control_cuped = y_control - model_control.predict(X)
post_metric_treatment_cuped = y_treatment - model_treatment.predict(X)

# A/B test results after applying CUPED
ab_diff_cuped = post_metric_treatment_cuped.mean() - post_metric_control_cuped.mean()
ab_std_cuped = np.sqrt(np.var(post_metric_treatment_cuped) / n + np.var(post_metric_control_cuped) / n)

# Visualization
plt.figure(figsize=(10, 6))
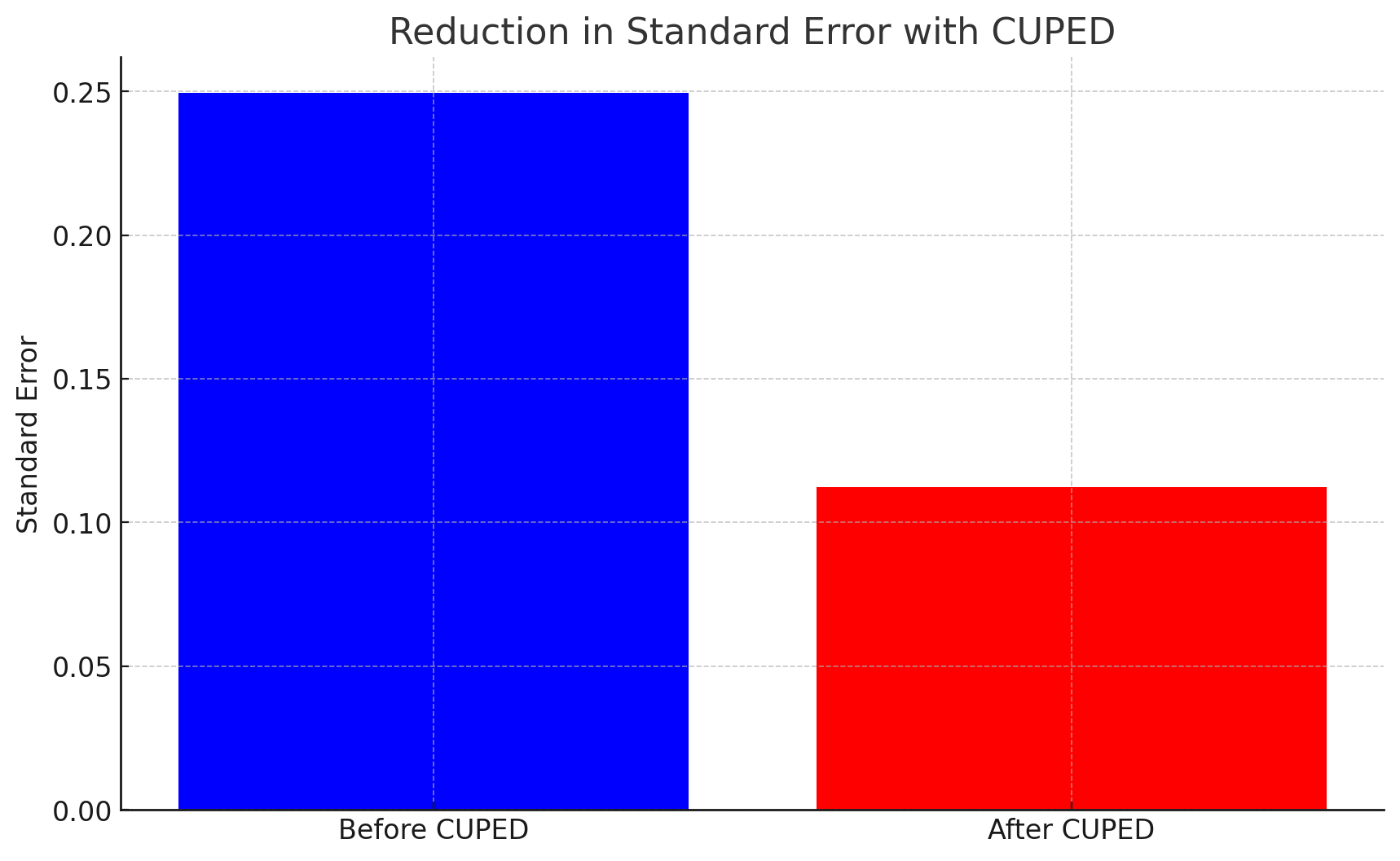
plt.bar(["Before CUPED", "After CUPED"], [ab_std, ab_std_cuped], color=['blue', 'red'])
plt.ylabel("Standard Error")
plt.title("Reduction in Standard Error with CUPED")
plt.show()
description

まず実験前の値として正規分布で乱数を発生させている。
そのあとに実験中の指標を再現するためにさらにノイズを加えたデータを作る。
単純な比較の場合はここで得られた値をそのまま分散として使う。
CUPEDを使う場合はここから実験前のデータのを用いて線形回帰を行い、予測値を用いて指標を補正している。
補正後のほうが分散が小さくなっていることがグラフからわかる。

まとめ

  • CUPEDを使うとA/Bテストの分散を削減し、より良い精度で検定を行うことが可能
  • 実験前のデータが使える & 相関を持っていることが必要

参考文献

1
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?