はじめに
二値分類の評価指標について
「AUCとGini係数ってどんな関係だっけ?」
と毎回忘れては調べているので、いい加減覚える意味で体系的にまとめてみる。
この記事では
- AUCとは何か?
- Gini係数とは何か
- 両者はどんな関係があるか?
を理解することを目的とする。
最初に結論
AUCとGini係数の間には
Gini=2AUC−1
の関係がある。
AUCは0.5から1の範囲を取るため、Gini係数は0から1までの範囲を取る。
どちらも値が大きいほど分類性能が良いことを表す。
最終的にこの式を理解することを目的としよう。
AUCを理解しよう
AUC (Area Under the Curve)は二値分類における有名な評価指標の一つであり、文字通り、「ROC曲線下の面積」を表す。
ROC曲線とは?
ROC (Receiver Operating Charastaristic Curve)は受信者操作特性と呼ばれるカーブを表す。
以下の図にあるようなカーブがROC曲線だ。(図はすべてWikipediaより拝借)

軸の定義はそれぞれ以下のようになる。
縦: 真陽性 (True Poritive) = 全体の正例のうち何%を正しく正例として分類できたか
横: 偽陽性 (False Positive) = 全体の負例のうち何%を誤って正例として分類してしまったか
どちらも正例と分類しているところがポイント。
True Positive, False PositiveはそれぞれTP、FPと表記されることもある。
また、正例を正しく正例と分類できたかを敏感度 (sensitivity)、負例を正しく負例と分類できたかを特異度 (specificity) とも呼ぶ。
つまり、
TP = \rm{sensitivity}, \\
\it{FP} =\rm{ (1-specificity})
である。
イメージ的には敏感度は陽性を見つけたい場合にどれくらい「敏感」な分類器であるか、特異度はどれくらい「特異=陽性とは異なっている」であるかと覚えておけば良い。
自分の場合はこの辺の細かい定義をすぐに忘れてしまうので、「縦をTP、横をFPでplotしたものがROCカーブ!」と覚えている。
二値分類としきい値
今回の議論したい評価指標である二値分類について考えよう。
ここでは「正例を正しく正例と判断し、負例を正しく負例と判断するためのしきい値」を考えよう。
例えば、病院の診断で特定の値がしきい値以上だった場合に病気と診断するなどが挙げられる。
しきい値をどのように設定すべきか、下の図を見ながら考えよう。
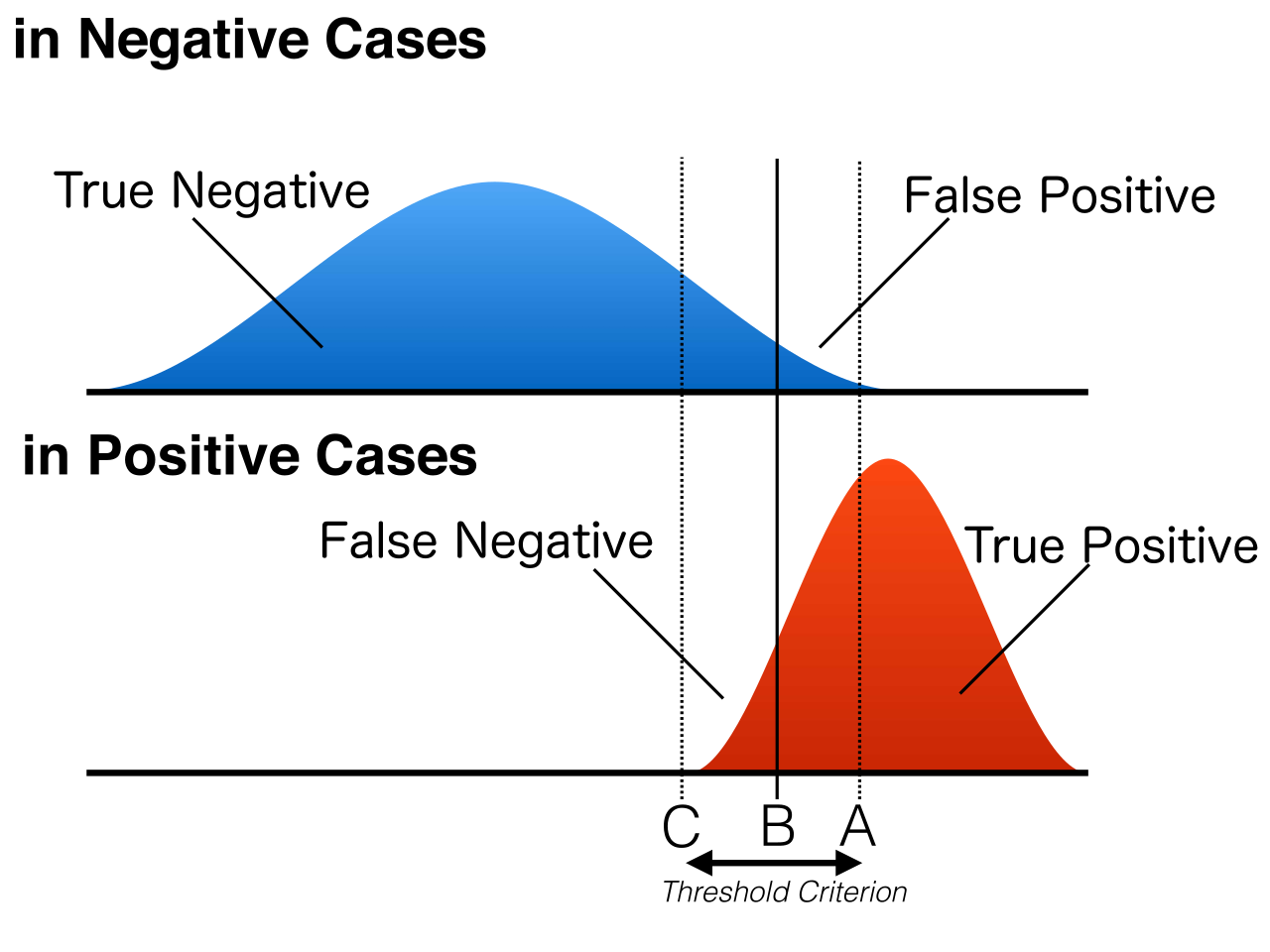
上の青い分布が負例、下の赤い図が正例を表す。
先ほど説明したTP, FPに加えて
- True Negative = TN = 負例を正しく負例と分類した
- False Negative = FN = 正例を誤って負例と分類した
が加わっていることをおさえよう。
この4パターンですべての場合を網羅できる。
さて、上の図において縦線のしきい値を指定し、この値を超えたサンプルを正例と判断することにしよう。
上の図においては、どのようなしきい値を設定しても正例と負例を完全に分類することは難しいことがわかるだろう。
例えばしきい値が左(図のC側)にある場合、FNを小さくできるがFPが大きくなってしまう。
逆にしきい値が右(図のA側)にある場合、FPを小さくできるがFNが大きくなってしまう。
このように、両者にはトレードオフの関係があり、FNとFPをしきい値操作によって同時に小さくすることができない。
しきい値をどちらに振るべきかはケースバーケースだ。
例えば健康診断の場合は健康な人を誤って病気と診断してしまうより、病気の可能性がある人を取りこぼすほうが危険だ。
(FPの場合は再検査すれば良いが、FNの場合は病気が進行して手遅れになる恐れがある)
したがって、しきい値は左寄りにすべきだ。
では裁判で判決を考える場合はどうだろう?
「推定無罪」の原則があるように、冤罪で死刑にしてしまっては取り返しがつかないためしきい値は右に振るべきだ。
これは犯罪者を無罪と判断してしまうリスクを許容することでもある。
AUCの導入
このしきい値の考え方を先ほどのROC曲線で考えよう。
ROC曲線の図に書いてあるABCがそのまま先ほどのしきい値で議論したABCに当てはまる。
しきい値をずらしていくことでカーブ上を推移する。
同じように、分類性能が高いほどこの曲線は上側を描くカーブになり、性能が低いと下側しなることもイメージできるだろう。
そして、完全にランダムに分類した場合(つまり、分類性能が最悪)の場合はy=xの直線を描くようになる。
これは分類性能の評価に使えそうだ。
でも
「ROC曲線が上側にあるから精度が良いっぽい」
とかだと定性的すぎて判断が難しい。
これをもっと定量的に数字で表せるようにしたい。
そこでROC曲線下の面積(つまりAUC)に着目する。
ROC曲線が上側にカーブを描くほど曲線によって作られる面積は大きくなるだろう。
AUCは1に近いほど分類性能が高く、0.5に近いほど精度が低いと言える。
これがAUCが二値分類の性能評価として使える理由である。
ROC曲線をPythonでplotしてみよう。
以下のコードで可視化してみる。
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
import numpy as np
# 仮の分類結果を生成
# y_trueは実際のクラスラベル, y_scoresはモデルの予測スコア
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
# ROC曲線のデータを計算
fpr, tpr, thresholds = roc_curve(y_true, y_scores)
roc_auc = auc(fpr, tpr)
# ROC曲線をプロット
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic Example')
plt.legend(loc="lower right")
plt.show()

オレンジの線がROC曲線で青い点線がランダムに分類したときの線である。
(この例だとサンプルが4つしかないので、曲線というよりはギザギザな直線だ)
オレンジの下側の面積が0.75なのでAUC=0.75となる。
コード中の
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
の部分について。
y_trueは仮にサンプルを順番にABCDとしたとすると、ABが負例でCDが正例であることを表す。
y_scoreは実際に予測したスコアだ。
図の原点から考えよう。
ここは先ほどの二値分類の図でいうと「しきい値を一番右側に振った状態 = すべてを負例と予測した場合」に相当する。
この場合は正例を正しく正例と認識できていないが、負例を間違って正例としてしまうことがない。
つまり(0,0)の点を表し、コードにおいてはしきい値を1と考えれば良いだろう。
さて、しきい値を0.7くらいまで下げたときを考えよう。
この場合、y_scoreを見ればABCを負例、Dを正例と識別することになるだろう。
CDと二つある正例のうちDを正しく分類できたのでTP=0.5になる。
さらにしきい値を0.38まで下げると、Dに加えて次にスコアの高いBも正例に分類されることになる。
だが、Bは本来は負例であるためFPの値が0->0.5になる。
同様にしてしきい値を0まで下げれば上図のオレンジの線の軌跡がそのまま出てくるだろう。
ここで、AUCを評価指標として使う場合の2つの重要な性質を抑えたい。
それは
- しきい値の場所によらず分類器全体の精度を評価できる
- 予測値の順番だけに左右され、値自体によらない
ことだ。
2点目について説明しよう。
例えばコードのy_scoresを以下のいずれの場合に変更しても、スコアの順番が変わらない限りAUCの値は変わらない。
y_scores = np.array([0.01, 0.8, 0.2, 0.99])
y_scores = np.array([0.50, 0.54, 0.53, 0.55])
逆にloglossなどのように"スコアそのもの"を利用する指標の場合はそれぞれ異なる値となる。
この場合は順番よりもむしろ「正例をできるだけ1に近い値、負例をできるだけ0に近い値」で予測することが重要になる。
同じ二値分類による評価指標でも微妙に性質が異なるのであるので覚えておこう。
データセットが正例や負例に極端に偏っている場合はloglossなど確率値をそのまま使うよりもAUCのように値の方が有効だ。
Gini係数を理解しよう
さて、長くなったが次にGini係数について考えよう。
Gini係数(ジニ係数)は二値分類の評価指標というよりは「社会における所得の不平等さを測る」という経済学的な背景から考えられた指標だ。
1912年にイタリアの統計学者、コッラド・ジニによって考案されたらしい。
Gini係数は誰か一人がすべての富を独占している状態を1、所得が均一で平等な状態を0とする。
要は社会における富がどれくらい偏っているかということだ。
これも図を見ながら考えよう。

横軸を左から右に、所得の低い人から順番に累積和を計算していくことを考えよう。
この累積和が図上に描く曲線をローレンツ曲線と呼ぶ。
仮にすべての人の所得が同じであれば、この曲線は斜め45度を描くように推移するだろう。
このときの線を均等分配線(Line of equality)という。
すべての人の所得が同じだった場合、「ローレンツ曲線と均等分配線は一致する」という言い方もできる。
一方で所得格差が激しければ、累積和はなかなか増えず、最後で一気に上昇するような曲線になるだろう。
図にあるように均等分配線とローレンツ曲線で囲まれる面積をA、ローレンツ曲線下の面積をBとしたとき、Gini係数は
\begin{align}
Gini &= \frac{A}{A+B} \\
&= 2A
\end{align}
と定義される。
(1行目から二行目はA+B=0.5であることを利用した)
もしごく一部の人に富が集中していた場合、Bの面積は限りなく0に近づくのでGini係数は1となる。
逆に完全に平等な場合はAの面積が0になるのでGini係数は0となり、最初の説明の感覚とも合う。
さて、これを富の不平等のではなく"分類"の観点で見るとどうなるだろう。
つまり、全人数を所得の合計が少ないグループと多いグループに分類したいと考える。
すべての人の所得が等しい場合は所得の偏りがあるように分けるのは難しいが、一部に富が偏っていれば簡単に分類できるだろう。
先ほどのROC曲線はカーブが上にあるほど精度が良かったが、ローレンツカーブの場合は下にあるほど精度が高いといえる。
AUCとGini係数の関係を理解しよう
ROC曲線とローレンツ曲線、やや近い形にはなってきた。
ROCとAUCの図を少し変形してみよう。

AUCがROC曲線以下の面積だったことを思い出そう。
ROC曲線とy=xの直線で囲まれた面積をAとおけば、これは
A = AUC - 0.5
と表すことができる。
そして縦軸と横軸を入れ替えればGini係数の説明で出てきた図と同じ形にできる。
Gini係数の図を低所得と高所得の分類とし、
「低所得の人間をちゃんと低所得としてカウントできるか?」
の問題と考えよう。
そうすれば縦軸、横軸を
- FP (本当は高所得なのに間違って低所得にカウントしてしまった)
- TP (低所得の人間をちゃんと低所得としてカウントできているか)
と(多少強引ではあるが)解釈できる。
ここでは低所得が正例にあたり、正確に低所得の人間だけを選べば累計所得は小さくなるとイメージすれば良い。
Gini係数は2Aとシンプルに表すことができたことを思い出そう。
すると
\begin{align}
2A = Gini = 2(AUC - 0.5) \\
Gini = 2AUC - 1
\end{align}
となり、当初目指していた式に辿りづけた!
結局のところ、別々の観点からスタートししたものの、AUCとGini係数は同じような指標だということだ。
単にAUCが0.5~1の範囲を取るのに対してGini係数は0~1の範囲を取るというだけということがこの式を見ればわかるだろう。
まとめ
- AUCは二値分類の精度を表す指標である (0.5~1の範囲)
- この値はしきい値に依らず、スコアの順番だけで決まる
- Gini係数は元々は経済の観点で提唱された指標である (0~1の範囲)
- 富の偏りを表す指標である
- $Gini = 2AUC - 1$の関係がある
余談
- Kaggleだと2018年のHOME CREDIT DEFAULT RISKのコンペでこの指標が用いられた
- 2024年、復刻版とも言えるようなコンペ(HOME CREDIT DEFAULT RISK MODEL STABILITY)が再び開催されているが、どのような指標を設定するべきかで公式に議論が巻き起こっているようだ