【機械学習】決定木を使ってFX予測をする

機械学習とFX

こんにちは。Qiitaにまともな記事を投稿するのは初めてです。
最近機械学習のお勉強をはじめました。
機械学習、もはや言うまでもないけど、いろんなところで使われますね。
スパムメールのフィルタリングや商品のレコメンドなどなど...実例を挙げればきりがないですね。
そんな中でも僕は機械学習を使った株価とかFXの予測に興味を持ったので、今日は
機械学習の１つである__決定木を用いてFXを予測__してみたいと思います。
もし良い精度で株価とかFXの予測できれば何もしなくても儲けることができるので非常に夢がある話ですよね。
ただ実際にはそんなに簡単に予測できるほど甘いものではないので、勝つ、儲けるというよりも最近勉強した機械学習を何かに適用したいというのが一番のモチベーションです。
なので最初に言っておきますが、もしこの記事を読んでる人で__「機械学習とかどうでもいいからAIでFXを予測して明日のドル円が上がるか下がるか教えてくれ！」__という人にとってはまったく有益な情報はないです。機械学習やFX予測に興味がある人にとってはもしかしたら少しだけ楽しめるかもしれません。その程度です。

FXって？

株の場合、株を購入して株価が上がれば儲かる、下がれば損をする、というのは誰でも知っていると思います。FXについてはもしかしたら知らない方もいるかもしれないので一応説明しておきます。
例えば１ドル100円で取引されていたとします。この状態で1ドルの「買い」注文を入れたとしましょう。
明日この1ドルが

• 110円に上がる→10円の利益
• 90円に下がる→しまえば10円の損失

ですよね。このような為替の取引のことをFXと言います。
FXの場合はレバレッジというものをかけることができるので、例えばレバレッジを10倍にすれば10倍のお金を動かすことができます。この場合利益も10倍、損失も10倍なので注意が必要です。
ドルと円の取引の場合はドル円と呼ばれ。1ドル100円->110円のようにドルの価値が上がればドル高（円安）となり、逆に1ドル100円->９0円のようにドルの価値が下がればドル安（円高）となります。
FXについてはわかりやすく説明している本やサイトなどが腐る程あるのでこれ以上は説明しませんが、要は株と同じように__上がるか、下がるかを予測できれば利益を生むことができる__ということです。

参考にしたサイト

ここを参考にしました。決定木の丁寧な説明もここに載っているので、この記事ではあまり詳しい解説はしないです。
一言で説明すれば、決定木には標準化と呼ばれる特徴量をスケーリングする作業がいらなかったり、どういう過程でその結果が得られたのかという解釈がしやすい（意味解釈性がある）などの利点があります。
リンク先のページで行われていることをざっくりとまとめます。

• 2018年時点での500日分の日足のドル円データを使って明日のドル円が上がるか下がるかを予測する
• 決定木を使う
• 他の分類器は使っていない。Grid Searchや交差検証などは行なっていない
• 素性として使ったのはドル円の「始値」「終値」「高値」「安値」
• トレーニングデータ（学習データ）とテストデータを8:2で分割している
• testデータに適用した結果、適合率は約50%だった。（あんまりうまく予測できてない）

といった感じです。
本気で予測するよりもあくまで機械学習（決定木）をFXに適用する方法を紹介することをメインとしているので、予測精度はそんなに高くないですね。

このページでやりたいこと

• 上で紹介したページと同様の方法を自分の環境で適用する
• 2019年終わりまでの最新の日足データを使う
• 何日分のデータを使うと精度がよくなるのかを調べたい（500日？200日？）
• 素性を増やすと精度が向上するかを確かめたい
• grid searchを使って決定木の最適なパラメータを求めたい
• 交差検証をちゃんと行う

といったところです。素性を増やすことについては、上のページでは数百日分のデータを学習していますが、実際に予測する際の素性として使っているのは「始値」「終値」「高値」「安値」の4つのみなんですよね。
つまり明日のドル円が上がるか下がるかを決める際に”その日の”ローソク足のみで判断して決めているわけです。
でも、実際にトレーダーが判断する際には移動平均（過去n日の平均値）やボリンジャーバンドやMACDなどと呼ばれるさまざまなテクニカル指標ってやつを使うことが多いんですよね。
そんなわけで、今回は以上の4つの素性に加えて__「5日、25日、50日、75日の終値の平均と分散」、「過去3日までの始値、終値、高値、安値」__などを新たに加えたいと思います。これらの値はさきほど言及したテクニカル指標に関連しています。
何を言っているかよくわからないって？
明日のドル円を予測する際に今日の値動きだけじゃなくて、過去数日〜数週間の平均値やどれくらいばらつきがあったかも参考にした方がいい予測ができるよね？ってことです。
すごくわかりづらい例えで言うと、
「今日のご飯はお母さんが作ってくれたカレーライスだった。過去の傾向からカレーライスの次の日のご飯はハンバーグである確率が高いので明日はハンバーグだ！」
と予測するのが上でやっている方法です。僕がやりたいのは
「今日のご飯はカレーライスだった。昨日は肉じゃが、先週は中華料理が多かった。今日のメニューと直近数週間の傾向から推測すると...明日はハンバーグ！」
って感じです。わかりづらいですね。

jupyterで実装してみる

前準備

上のページと同じようにjupyterでPythonを使ってごりごり書きます。
途中までは上で紹介したページとほぼ同じですが、順番にやっていこうと思います。
まずは必要なライブラリをいろいろとimportします。

import pandas as pd
import numpy as np 
# データ可視化のライブラリ
import matplotlib.pyplot as plt
# 機械学習ライブラリ
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
# graphvizのインポート
import graphviz
# grid searchとcross validation用
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV

下２つはgrid searchや交差検証を行うときに必要です。次にデータを読み込みます。
今回は2017年から2019年までの2年分のcsvデータを用意しました。
僕はMT4というソフトで取引を行なっているのですが、そこで提供されているデータをcsv形式で持ってきました。

# CSVファイルの読み込み。2017-2019の２年分
df = pd.read_csv('usd_jpy_api_2017_2019.csv')
# 最後の5行を確認
df.tail()

最初の5行はこんな感じです。それぞれ取引が行われた時間、終値、始値、高値、安値、取引量を表してます。

ここらへんまでの作業は上で紹介したページなのでざっくりと飛ばしていきますが、ついの日の終値が上がるかどうかで正解ラベルを0, 1で付与します。

# 翌日終値 - 当日終値で差分を計算
# shift(-1)でcloseを上に1つずらす
df['close+1'] = df.close.shift(-1)
df['diff'] = df['close+1'] - df['close']
# 最終日はclose+1がNaNになるので削る
df = df[:-1]

一応上昇、下降データの割合を確認してみます。

# 上昇と下降のデータ割合を確認
m = len(df['close'])
# df['diff']>0で全行に対してtrueかfalseで返してくれる。df[(df['diff'] > 0)]でdff>0に絞って全てのカラムを出力
print(len(df[(df['diff'] > 0)]) / m * 100)
print(len(df[(df['diff'] < 0)]) / m * 100)

52.16284987277354
47.837150127226465

わずかに上昇した日の方が多いですね。次に不要な列を削除してラベルの名前をtargetにします。

• targetと書いてあるのが学習する際に必要な正解のクラスラベルにあたる
• 次の日の終値が上がる場合は1、下がる場合は0が割り当てられている

df.rename(columns={"diff" : "target"}, inplace=True)
# 不要なカラムを削除
del df['close+1']
del df['time']
# カラムの並び替え
df = df[['target', 'volume', 'open', 'high', 'low', 'close']]
# 最初の5行を出力
df.head()

素性の追加

ここから新しい素性を計算してゴリゴリ追加していきます。

# 移動平均の計算、5日、25日、50日、75日
# ついでにstdも計算する。（=ボリンジャーバンドと同等の情報を持ってる）
# 75日分のデータ確保
for i in range(1, 75):
    df['close-'+str(i)] = df.close.shift(+i)
# 移動平均の値とstdを計算する, skipnaの設定で一つでもNanがあるやつはNanを返すようにする
nclose = 5    
df['MA5'] = df.iloc[:, np.arange(nclose, nclose+5)].mean(axis='columns', skipna=False)
df['MA25'] = df.iloc[:, np.arange(nclose, nclose+25)].mean(axis='columns', skipna=False)
df['MA50'] = df.iloc[:, np.arange(nclose, nclose+50)].mean(axis='columns', skipna=False)
df['MA75'] = df.iloc[:, np.arange(nclose, nclose+75)].mean(axis='columns', skipna=False)

df['STD5'] = df.iloc[:, np.arange(nclose, nclose+5)].std(axis='columns', skipna=False)
df['STD25'] = df.iloc[:, np.arange(nclose, nclose+25)].std(axis='columns', skipna=False)
df['STD50'] = df.iloc[:, np.arange(nclose, nclose+50)].std(axis='columns', skipna=False)
df['STD75'] = df.iloc[:, np.arange(nclose, nclose+75)].std(axis='columns', skipna=False)
# 計算終わったら余分な列は削除
for i in range(1, 75):
    del df['close-'+str(i)]
# それぞれの平均線の前日からの変化（移動平均線が上向か、下向きかわかる）
# shift(-1)でcloseを上に1つずらす
df['diff_MA5'] = df['MA5'] - df.MA5.shift(1) 
df['diff_MA25'] = df['MA25'] - df.MA25.shift(1) 
df['diff_MA50'] = df['MA50'] - df.MA50.shift(1) 
df['diff_MA75'] = df['MA50'] - df.MA50.shift(1) 
# 3日前までのopen, close, high, lowも素性に加えたい
for i in range(1, 4):
    df['close-'+str(i)] = df.close.shift(+i)
    df['open-'+str(i)] = df.open.shift(+i)
    df['high-'+str(i)] = df.high.shift(+i)
    df['low-'+str(i)] = df.low.shift(+i)
# NaNを含む行を削除
df = df.dropna()
# 何日分使うか決める
nday = 500
df = df[-nday:]
# df.head()
df

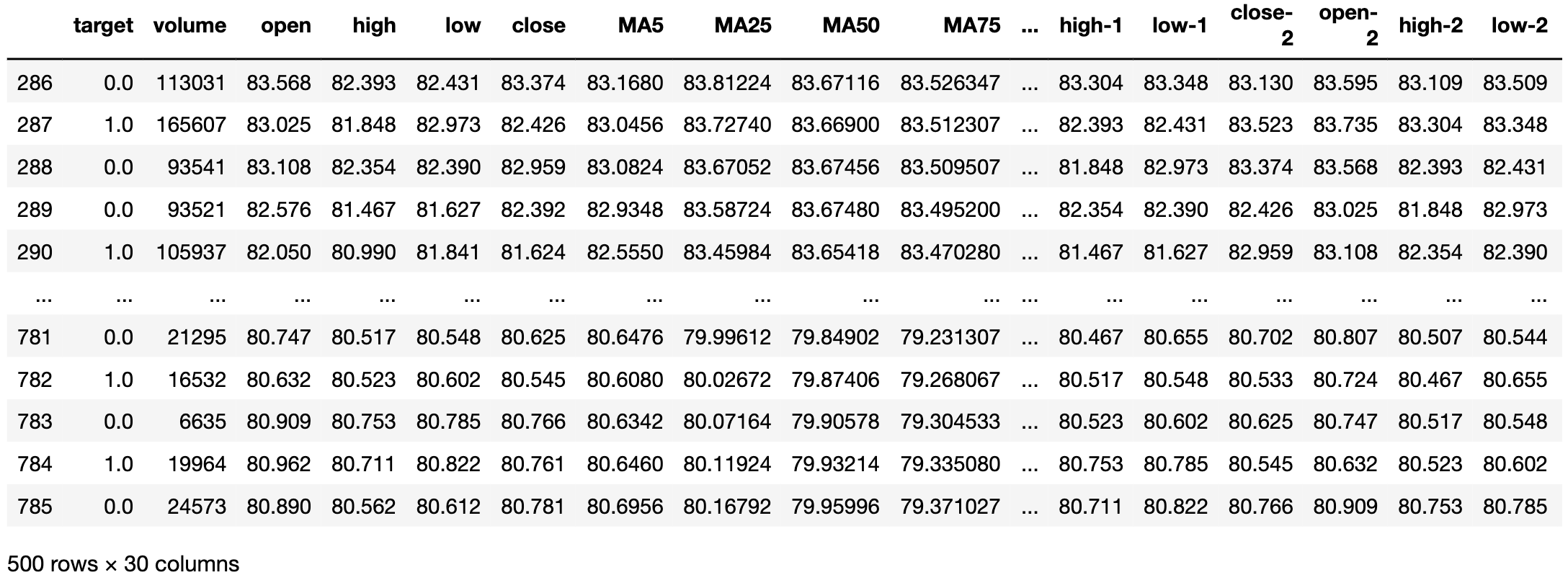
右の方見切れてますが、こんな感じです。

• MAと書いてあるのは移動平均。例えばMA5はその日から過去5日間での終値の平均
• close-nはn日前の終値を表す（openやhigh、lowも同様）
• STDとかいてあるのは標準偏差
• 移動平均が上を向いているのか、下を向いているのかも知りたかったので前日からの変化もdiff_という名前で加えた

とりあえず500日分のデータを選びました。
最初にデータを読み込んだ時に指定してもよかったんですが、75日平均を計算するときなどは75日分遡ったデータが必要となるので、一通り計算が済んでから500日分のデータを使っています。これで500行30列のデータができあがりました。

決定木の学習

準備は整ったので、trainとtestに分割して評価していこう。

n = df.shape[0]
p = df.shape[1]
print(n,p)
# 訓練データとテストデータへ分割。シャッフルはしない
train_start = 0
train_end = int(np.floor(0.8*n))
test_start = train_end + 1
test_end = n
data_train = np.arange(train_start, train_end)
data_train = df.iloc[np.arange(train_start, train_end), :]
data_test = df.iloc[np.arange(test_start, test_end), :]
# 訓練データとテストデータのサイズを確認
print(data_train.shape)
print(data_test.shape)

今回は8:2で分割しました。

(400, 30)
(99, 30)

次に正解ラベルの部分を分離して、決定木で学習を行なっていきます。
木の深さを表すハイパーパラメータであるmax_depthはとりあえず5にしてありますが、適切な値はこの後grid searchで決定します。

# targetを分離
X_train = data_train.iloc[:, 1:]
y_train = data_train.iloc[:, 0]
X_test = data_test.iloc[:, 1:]
y_test = data_test.iloc[:, 0]
# 決定技モデルの訓練
clf_2 = DecisionTreeClassifier(max_depth=5)

ようやく決定木が出てきましたね。k=10の交差検証とgrid searchを行います。

# grid searchでmax_depthの最適なパラメータを決める
# k=10のk分割交差検証も行う
params = {'max_depth': [2, 5, 10, 20]}

grid = GridSearchCV(estimator=clf_2,
                    param_grid=params,
                    cv=10,
                    scoring='roc_auc')
grid.fit(X_train, y_train)
for r, _ in enumerate(grid.cv_results_['mean_test_score']):
    print("%0.3f +/- %0.2f %r"
          % (grid.cv_results_['mean_test_score'][r],
             grid.cv_results_['std_test_score'][r] / 2.0,
             grid.cv_results_['params'][r]))
print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)

出力はこんな感じ。深さ10の時が一番正答率高くで69%と出ていますね。

0.630 +/- 0.05 {'max_depth': 2}
0.679 +/- 0.06 {'max_depth': 5}
0.690 +/- 0.06 {'max_depth': 10}
0.665 +/- 0.05 {'max_depth': 20}
Best parameters: {'max_depth': 10}
Accuracy: 0.69

テストデータでの評価

上で出てきた正答率はあくまで学習データでの正答率なので、testデータを予測できるか試してみます。

# grid searchで最適だったパラメータを使って学習する
clf_2 = grid.best_estimator_
clf_2 = clf_2.fit(X_train, y_train)
clf_2

パラメータはこんな感じで設定されていることがわかる。

DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=10,
                       max_features=None, max_leaf_nodes=None,
                       min_impurity_decrease=0.0, min_impurity_split=None,
                       min_samples_leaf=1, min_samples_split=2,
                       min_weight_fraction_leaf=0.0, presort=False,
                       random_state=None, splitter='best')

せっかくなので可視化してみよう。max_depth=1０なのでえぐいことになっとる。。
一番上の部分だけ切り取るとこんな感じ。
この場合だと3日前の高値が82.068以上なのか以下なのかで最初に分割を行い、次に当日の安値でしきい値を決めて分割してってるのがわかる。
giniと買いてあるのは、gini不純度という値が小さくなるように分割を行なっているという意味。
value=の部分は上昇、下降それぞれいくつあるかを表す。

testの正答率を調べてみよう。

pred_test_2 = clf_2.predict(X_test)
# テストデータ 正解率
accuracy_score(y_test, pred_test_2)

0.555555555555

うーん。。いろいろ頑張った割には..って感じだけど、まあこんなもんか。
どの素性が重要なのか（feature impotance）もみてみよう。

# 重要度の高い素性を表示
importances = clf_2.feature_importances_
indices = np.argsort(importances)[::-1]

for f in range(X_train.shape[1]):
    print("%2d) %-*s %f" % (f + 1, 30, 
                            df.columns[1+indices[f]],
                            importances[indices[f]]))    

移動平均とか色々計算してはみたけど、結局当日とか前日の値動きが重要みたいね。

 1) low                            0.407248
 2) close                          0.184738
 3) low-1                          0.078743
 4) high-3                         0.069653
 5) high                           0.043982
 6) diff_MA5                       0.039119
 7) close-3                        0.035420
 8) STD50                          0.035032
 9) diff_MA25                      0.029473
10) MA75                           0.028125
11) MA50                           0.009830
12) open-3                         0.009540
13) STD25                          0.009159
14) low-3                          0.007632
15) high-1                         0.007632
16) volume                         0.004674
以下0なので略

いろいろ値をいじってみる

今回の検証の条件を今一度まとめてみよう

• 集計期間：2019年12月31日までの500日分

• 分類器：決定木

  • パラメータ：max_depth=10

• 交差検証：10分割

• トレーニングとテストの分割：8:2

• 結果：正答率0.55
  ここで決定木のパラメータはgrid searchで決めたのでいいとして、集計期間や分割の比率などはいじれそうなので試してみました。

• 分割比率を9:1に変えた結果　→ 正答率:61% (max_depth=20)

• 集計期間を200日にした結果 → 正答率:56% (max_depth=10)
  となりました。正答率は50-60%くらいってとこですかね。
  grid searchは条件を変えるたびにやり直してますが、だいたいmax_depth=10-20くらいが一番いいスコアでした。

今回わかったこと

• ドル円の日足データから決定木でいろいろ頑張って予測するととだいたい50-60%くらいの精度がでる

今後やりたいこと

• 決定木以外の分類器で試す （ロジスティック回帰、kNN、etc.）
• アンサンブルの手法を使う （いくつかの分類機を組み合わせる。）
• 次元削減などを適切に行う　（今回は決定木の性質上あまり必要なかった）
• 素性を考える　（もっといい特徴量があるかも...??）

思ったより長くなってしまった。。
おわり