きっかけ
最近ひろゆきが以下のようなツイートをしていた。
「人間が生涯に払う税金は4000万円、国が1000万円払っても元は取れるどこかプラスになる」
とう旨のもの。
政治的な是非は置いといて、効果検証の題材としてちょうどいいなーと思ったので、これを元に効果検証の考え方を一通り紹介したい。
注意事項
子どもを作る/作らないというのは非常にセンシティブな問題だ。
なんらかの信条で作らない人もいるだろうし、健康上の理由で欲しくてもできない人もいる。
ここではそう言った子供を作ること自体の是非を問うつもりはないし、政治的な意見を述べるつもりもない。
この記事の目的は「子どもができたら1000万円を配る」という施策が「税収アップに対して有効か」という単純化された問題設定に対してどうアプローチするのが適切かを考えることなので、ご容赦いただきたい。
効果検証ってなに?
ざっくり言えば、「なんらかのマーケティング施策を打った時に、どれくらいの効果があったかを測る」ことだ。
今回は「子ども1人につき1000万配る」という施策を行った時にどれくらい効果が出るかを知りたいわけだ。
実はこういう効果を測りたいケースはビジネスシーンだと非常に多い。
例えばあなたがピザ屋さんだとして、「割引クーポンのチラシを配るとピザの売り上げが増えるか?」という効果を知ることは重要だ。
もしクーポンが効果的であればたくさんチラシを配りたいだろうし、効果がなければ辞めたい。
このように、効果検証の結果は今後の意思決定を左右し、企業の利益に大きく関わる。
今回の例で言えば「将来の日本の税収はプラスになるか?」というかなりスケールの大きな問題を考えることになる。
そんなに簡単なものではない
まず最初に言っておきたいのは、このような効果を測るのは決して簡単なことではないということだ。
ひろゆきのツイートを見ると、「1000万配って4000万の税収が得られるなら確かにお得だ」と簡単に納得してしまう人もいるかもしれないが、今一度しっかり考えてみてほしい。
「子どもができたら1000万配ります」と宣言したところで、最初から子どもを作るつもりがない人には響かないだろう。
つまりこういった人たちは効果がない。
また見落としがちなのが、1000万円を貰える/貰えないにかかわらず子どもを作る予定の人もいるだろうということだ。
こういった人たちにお金を配ったところで税収アップにはつながらないどころが、(今回の問題設定においては)1000万円をドブに捨てることになってしまう。
4パターンで考える
話を整理しよう。
今考えられるのは
- 1000万円を配る施策をする/しないの2パターン
- 各条件で実際に子どもをつくるかどうかの2パターン
の掛け合わせの4パターンである。
これを図にしたのが以下だ。

説得可能
- 1000万を貰えないなら子どもは作らないが、もらえるなら作りたい人たち
- この人たちに1000万円を配れば効果的に税収アップが期待できる
無関心
- 1000万を貰える/貰いないに関わらず、子どもを作るつもりがない人たち
- 子どもを作らない理由/事情については非常にセンシティブな話題であるためここでは触れない
- 「子どもを作ったら1000万円貰える」という施策の性質上、無関心なユーザーの存在は結果に寄与しない
テッパン
- 1000万を貰える/貰いないに関わらず、子どもを作るつもりの人たち
- この人たちはお金を配らなくても子供を作るため、1000万配っても税収アップにはつながらない
天邪鬼
- 1000万を配ると逆に子供を作る気がなくなる稀有な人たち
さて、ここから見えてくることがいっぱいあるが、特に重要なのが「説得可能」と「テッパン」だ。
まず、天邪鬼な人は無視できる。
というのも、「もともと子ども作る気だったけど、1000万円貰えるなら作らなくていいや」という思考の持ち主は普通に考えていないだろうし、もしいるとしても無視できるくらい少数だろう。
また、無関心な人も無視できる。
今回の施策は「1000万円をまず配って、子供が増えるといいな」ではなく、「子どもをつくると1000万円あげますよー」というルールを作ることなので、そもそも子どもができなければ1000万が配られない。
その場合、税収アップにもつながらないが、出費にもならない。
国からすると収入、支出の両方がゼロということだ。
なお、これは今回の問題設定においては無視できるという話なので、問題設定次第では異なることには注意が必要だ。
例えば最初の「ピザ屋さんのチラシ」の例だと、チラシを配るコストが発生するため、無関心なユーザーの存在も考慮する必要があるだろう。
まとめると、施策を成功させるカギはは「説得可能」な人にできるだけ増やして「テッパン」をできるだけ減らすことにある。
それを踏まえて上の図をもう一度眺めてみると、あることがわかってくる。
「説得可能」も「テッパン」も1000万を配った場合の結果は同じで、「配らなかった場合の結果」のみが異なる。
つまり、これらを分離しようと思ったら配った場合の結果だけでなく「配らなかった場合」の結果が必要ということだ。
直感的には(1000万を配った場合の税収)-(1000万を配らなかった場合の税収)を計算すれば、施策による効果が見えてきそうだ。
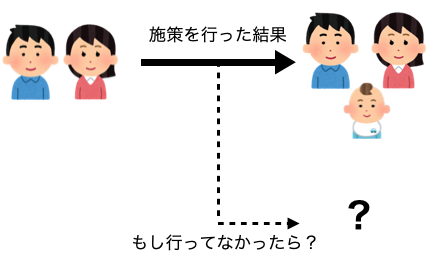
反実仮想をどうやって表現するか?
当たり前だが、特定の人に対して「1000万円を配った場合」と「配らなかった場合」の両方の結果を知ることは不可能だ。
1000万円を配って実際にその人が子どもを作ったとして、もし配らなかった場合にどうだったかを知ることはできないということだ。
よくあるアイディアとして、介入した後に上がったかどうかを確かめればいいのではないか?というものがある。
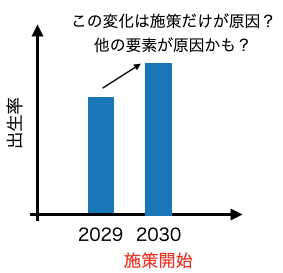
例えば2030年からこの施策を開始したとして、2029年と比べて出生率が上がっていれば施策が効果あったのではないか、というアイディアだ。
しかし、これは十分とは言い難い。
2030年に出生率が上がったは何か別の要因かもしれないからだ。
例えば、「2029年に比べて2030年の景気が上向いた」など別の要因によって出生率が上がった可能性もあり、今回の施策による効果がどれくらいか?を
見積もるのはすごく難しい。
ここで広く用いられる方法として、統計学を使った方法がある。
まず、母集団を「介入群」と「非介入群」に分ける。
例えば10000人いたとして、ランダムに5000人に1000万円配る(=介入する)ことにし、5000人には何も配らない。
そして1000万を配った群の平均の出生率が上がれば、効果があったと言えそうだ。
このアイディアの良いことろは、介入群と非介入群を同じ時期、同じ条件で比較することができるということだ。
つまり、先ほどの例のような「2029年と2030年の違い」のような要素を排除することができる。

webサービスなどではこのような手法はA/Bテストと呼ばれており、さまざまなサービスで広く行われている。
例えばAmazonのようなECサイトで新しい仕組みをリリースする時に、A/Bテストを行って新しい仕組み有効だとわかった場合のみリリースする、
といった具合だ。
有名な話だと、かつてGoogleがハイパーリンクの適切な色を調べるために41種類もの青色でA/Bテストを行い、一番クリック率が高かった青色を採用した、という例がある。
Googleはこれにより2億ドルの広告収入が増えたらしい。
式で表してみよう
さて、効果検証の分野では介入したユーザー群ことを"treatment group"、介入しない場合を"control group"と言う。
今後はそれぞれをtreat, ctrlと呼ぶことにする。
また、それぞれの対象となる人数を$N_{treat}, N_{ctrl}$と置くことにしよう。
また、treat, ctrlそれぞれにおいてどれくらいの割合の人が将来的に子どもを作るか(つまり出生率)をBTR (Birth Rate)として定義してみる。
例えば$BTR_{ctrl}=0.4$であれば、100人中40人が将来的に子供をつくる、という意味になる。
介入した場合は出生率が上がることが見込まれるため$BTR_{treat} > BTR_{ctrl}$となるはずだ。
今回の介入によってどれくらい人口が増えるかは
N_{treat}(BTR_{treat} - BTR_{ctrl})
によって計算可能だ。
もし最終的に全国民に適用された場合は$N_{treat}$は日本の人口と等しくなり、$N_{ctrl}=0$となる。
ここで、一人当たりの税収をIと定義する。
最初の前提だとI=4000万円となる。
そうすれば得られる税収は
I*N_{treat}(BTR_{treat} - BTR_{ctrl})
となる。
一方で必要なコストはどれくらいになるだろうか?
一人当たりに配る金額をMと定義してみる。(今回はM=1000万円となる)
このとき
M*N_{treat}BTR_{treat}
となる。
したがって
(得られる税収) - (費用)
は
I*N_{treat}(BTR_{treat} - BTR_{ctrl}) - M*N_{treat}*BTR_{treat}
で計算可能だ。この値がプラスになればお得、マイナスになれば損となる。
ちょっとわかりづらいので実際に数値を入れてみよう。
現在の日本の出生率は1.34なので、$BTR_{ctrl}=1.34$とおく。
仮にこの施策によって出生率が1.5まで上昇したとしよう。
すると$BTR_{treat}=1.5$となる。
施策対象者を日本全体とすると、男女2人ペアで考えるので、日本の人口1億2000万を2で割って$N=60,000,000$とおく。
これで得られる税収を計算できそうだ。
\begin{align}
I*N_{treat}(BTR_{treat} - BTR_{ctrl})&=40,000,000*60,000,000*(1.50-1.34)\\
&= 384,000,000,000,000
\end{align}
となり、384兆円のプラスになる。
一方でかかる費用は
\begin{align}
M*N_{treat}*BTR_{treat}&=10,000,000*60,000,000*1.5\\
&=900,000,000,000,000
\end{align}
となり、900兆のマイナスとなる。
どうやら出生率を1.34->1.5に上げたくらいだと損になってしまうようだ。
可視化してみよう
上の計算は1.5という数字を適当に入れただけなので、どれくらい出生率が上がれば元が取れるのか、可視化してみよう。
import matplotlib.pyplot as plt
def income(I, N, BTR_t, BTR_c):
return I*N*(BTR_t - BTR_c)
def cost(M, N, BTR_t):
return M*N*BTR_t
x = []
# 人口/2
N = 60000000
# 1000万配る
M = 10000000
# 4000万の税収
I = 40000000
# 日本の出生率
BTR_c = 1.34
# ctrlと同じ値で初期化
BTR_t = BTR_c
income_list = []
cost_list = []
diff_list = []
for i in range(14):
BTR_t = BTR_t + 0.01 * i
x.append(BTR_t)
_income = income(I, N, BTR_t, BTR_c)
_cost = cost(M, N, BTR_t)
income_list.append(_income)
cost_list.append(_cost)
diff_list.append(_income - _cost)
plt.plot(x, income_list, marker = 'o', color='b', label="income")
plt.plot(x, cost_list, marker = 'o', color='r', label="cost")
plt.plot(x, diff_list, marker = 's', color='g', label="income-cost")
plt.title('Hiroyuki Simulation', fontsize = 20)
plt.xlabel('Treatment Birth Rate', fontsize = 16)
plt.ylabel('Money', fontsize = 16)
plt.legend()
plt.grid(True)
plt.show()
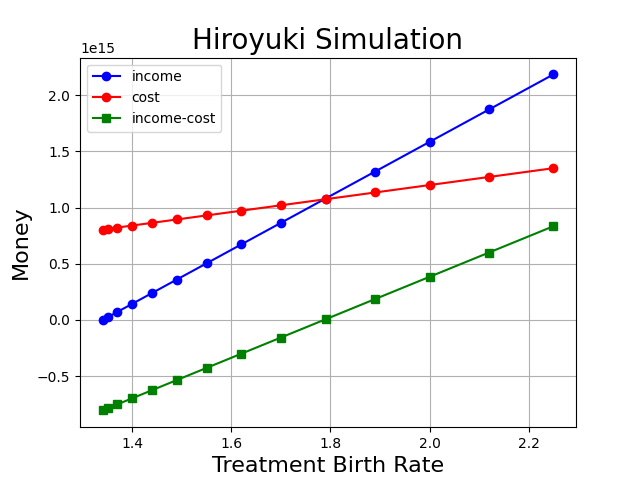
こんな感じ。
横軸は出生率。
青は税収、赤は費用、差分を緑で表示してある。
図を見ると、出生率が1.8を越えたあたりで差分がプラスになっている。
つまり、1000万円を配って利益を出すには出生率を1.34->1.8以上に上げる必要があるということだ。
とりあえず1000万円配ればOKというわけではないっぽい。
Uplift Modelingを用いた手法
上記のsimulationは最終的にすべての人に施策を適用した場合を考えているが、もう少し効率的な方法はないだろうか?
前述の議論で、「説得可能」な人には施策を実行したいが、「テッパン」には実行したくない、という話があった。
つまり、必ずしも全員に施策を適用する必要はなく、効果がありそうな人だけに絞れば良さそうだ。
実は機械学習などの手法を使えば、「説得可能」な人を優先して施策を実行することが可能になる。
上で議論した数式ではtreat, ctrl群それぞれに対してBTRを計算したが、もし一人一人に対して
$BTR_{treat}$, $BTR_{ctrl}$を計算することができれば、そのユーザーが「施策を介入した時だけ子どもを作るか?」を計算することが可能になる。
具体的には一人一人に対して$BTR_{treat} - BTR_{ctrl}$(これをuplift scoreという)を計算し、この値が大きい順に介入すれば良い。この方法をUplift Modelingという。
一人一人の「年収」「性別」「年齢」などを特徴量として学習すれば、uplift scoreを精度良く求められるだろう。
webサービスなどではこれらの手法は広く用いられている。
詳しく知りたい人は[1]などの書籍を参考にしてほしい。
現実問題としてどうすればいいか?
さて、復讐も兼ねて、ここまで紹介してきた2種類の手法を振り返る。
一つ目はA/Bテストだ。
最終的に全国民を対象に施策を実施する場合でも、事前にA/Bテストを行うことで施策の効果を検証できる。
treatの対象人数を少なくすることで、もし効果がなかった場合のダメージを軽減することが可能になるだろう。
施策が有効であった場合のみ実際に適当すれば良い。
二つ目はUplift modelingだ。
treat, ctrl両方のデータで学習することで、一人一人についてuplift scoreを計算することができる。
一度upliftスコアがもとまれば、スコアの高い順に○○%などの条件を付けて施策を実行すれば良い。
さて、いずれにせよ効果を見積もるには全国民を「介入群」と「非介入群」に分けたデータを取得する必要がある。
前述webサービスの例と同じように、今回の問題で同じ手法が行えるだろうか?
結論から言えば不可能ではない。
過去の事例で言えば、コロンビアの大学で「学費の割引券をランダムに配る」という介入を行うことで、学生の学費を軽減することの効果を見積もった例などがある。[2]
今回で言えば、例えば「ランダムに100万人を抽出して、子どもが生まれたら1000万円キャンペーン」などをを実施する、といった方法が考えられる。
だが実際に注意しなければならない点として、人によって待遇が違うため不平等であるとクレームが湧く可能性がある。
またこの問題は時に倫理面にも関連しており、例えば過去には「医療の効果を確認するため、あえて一部の人に必要とされる医療を提供しない」といった実験が行われたこともあった。
現在ではこのような実験は人道的観点から禁止されているが、社会福祉などに関わる施策を実行する場合は注意する必要がある。
(やや衝撃的な内容なのでメンタルが弱い人にはお勧めしないが、気になる人はタスキギー梅毒実験でググってみてほしい。)
セレクションバイアスと問題点
ランダムに対象を選んで介入を行うことをRCT (Randomazied Controlled Trial)という。
できればRCTを使ってtreat, ctrl群に分けた検証を行うことが望ましいが、なんらかの事情により行えないこともある。
例えばRCTのシステムを実装すること自体にコストがかかる場合や、前述の倫理的問題などによるものだ。
RCTが行えない場合の代替案はいくつかあるが、いずれにせよ大事なのは「セレクションバイアス」をなくすことだ。
セレクションバイアスとは介入を行う/行わないの母集団の決定の際に入り込むバイアスのことだ。
例えばツイッターのアンケートで「あなたはツイッターを使ったことがありますか?」というアンケートをとった場合、100%の人間がYesと答えるだろう。
だが、これをもって「すべての人間はツイッターを使っている」と結論付けるのは明らかに間違いだ。
これはアンケートをとる母集団の決定に「ツイッターユーザーである」というバイアスが入ってしまうためだ。
生存者バイアスと呼ばれるものもこの一つである。
以下の(有名な)画像は戦争中に帰還した飛行機の被弾した位置に赤いマークを付けたものだ。
ぱっと見赤いマークの被弾した箇所の装甲を強化する必要がありそうだが、実際には「赤いマークのない箇所の装甲を強化せよ」という命令が下されたというもの。
赤いマークの付いていない箇所に被弾した飛行機は帰還できなかったと考えられるため、本当に致命傷となるのはむしろ被弾していない箇所、というわけだ。
なお、この逸話が実話ではないという指摘もあるが、ニュートンのりんごのようなもので実話かどうかは本質的でないと個人的に思っている。
画像は以下のもの

今回の施策に関して言えば、例えば所得制限を付けて「所得が○○万円以下の人だけに施策を実行しよう」といったケースが考えられるが、これも「所得」を基準としたバイアスが入ってしまうため正しく効果を見積もれないことがある。
これに対処するための方法はいくつかあるが、詳しく知りたい人は[3]の書籍をあたってほしい。
このように、treat, ctrl群に分けた検証を行うためのハードルは高い。
そもそも上記のUplft Modelingを現実的に行えるか?という点も怪しい。
AIによって計算されたよくわからないスコアを基準にお金をもらえる/もらえないを決定することに関しては不満の声は大きいだろう。
さらに言えば、もし機械学習の結果、特定の性別や人種に偏ってスコアが高くなってしまった場合、差別問題にも発展してしまう恐れもある。
実際にAmazonは過去に優秀な人だけを書類選考通そうとした結果、意図せず「男性の方が女性より受かりやすい」という結果になってしまい、問題になった。
したがってこれらの手法を直接適用するのは難しそうだ。
現実的な落とし所
散々議論しておいてあれなのだが、結局のところ本当に実行しようと思ったら所得制限を設けるというのが一番手軽だと思われる。
理由は主に3つあって
- 実装コストが容易
- 国民に説明がしやすい
- 富裕層ほど「テッパン」が多く、貧困層ほど「説得可能」な人が多いと思われるため、効率が多い
特に3つ目については、所得が低い人に優先的に配ることで、Uplift scoreが高い人に介入したのと同じような効果が見込める。
RCTを用いた正確な効果検証が難しい場合、このへんが落とし所なのかなと思う。
まとめ
- 条件を付けずに「子どもが生まれたら1000万円」施策を実行した場合、出生率を1.8以上に上げないと元は取れない
- 所得に制限をつけることで、現実的で効率良い施策を実行できそう
- ちゃんと効果検証をするならtreat/ctrl群に分けて効果を見積もることができると良い
参考書籍
[1]仕事で始める機械学習
[2]効果検証入門
[3]A/Bテスト実践ガイド