はじめに
A/Bテストをやるときに避けて通れないのがt検定をはじめとする統計的仮説検定(以下仮説検定) だ。
QiitaだとRやPythonを使ってt検定を実践しているページはたくさんあったが、
「t検定とは何か」
「そもそもなぜそんなものが必要なのか?」
にフォーカスを当てた記事があまりなかった。
そこで、この記事ではA/Bテストにおけるt検定をゼロから理解することを目的にする。
Pythonを用いたおけるコードを用いた説明も最後に少し載せている。
この記事はt検定をよく聞く or 使ったことがあるけどいまいち何なのか掴めてない人や、そもそも統計何もわからない人をターゲットに想定している。
A/Bテストとは?
この記事では基本的にA/Bテストにおける統計検定を想定しているので、まずはA/Bテストについて説明しておく。
例えばあるECサイトで飲み物を売っているとする。
サイト内において、現在文字の色を青にしているが、文字色を赤にしたら売り上げが増えるかどうかを知りたいとする。

どうやったらこの効果がわかるだろうか?
一番わかりやすいのはとりあえずAからBに変更してみて、売り上げや クリック率(CTR) などの指標(メトリクスと呼ぶ)が上がるかどうかを調べてみることだ。
例えば文字の色を赤にして売り上げが上がればそのまま赤い文字を採用し、下がってしまった場合は青に戻せばいい。
要は文字色を変更した時のメトリクスの変化を見れば良いわけだ。
でも、これって実はすごく効果を見るのが難しい。
例えばBに変更している間だけ物凄い猛暑日で、たまたま飲み物がバカ売れしたとする。
そうすると、文字色が赤だから売れたのか?、それとも猛暑日だから売れたのか?の切り分けができなくなってしまう。
これを解決するのがA/Bテストだ。
サイトに訪れるユーザーをランダムにAとBに半分ずつ振り分け、それぞれでメトリクスを計算するのだ。
例えば10000人のユーザーが訪れたとして、5000人をA(青色表示)、もう半分の5000人にはB(赤色表示)を見せる。
その結果、もし赤を見せた5000人の方が売り上げやCTRが高ければ、B案を採用すればいいことになる。
A/Bテストを行えば先ほどの「たまたま猛暑日だった」のような違いを取り除き、ほぼ同じ条件での比較が可能になる。
仮説検定の必要性
ところがA/Bテストを行ったとしても、結果の判断はそう簡単なものではない。
Aの方が売り上げ10,000円、Bの方が売り上げ100,000円(売り上げ10倍!)だとしたら明らかにBを採用したほうが良さそうだ。
でもAの売り上げが10,000円、Bの売り上げが10,100円だったらどうだろうか?
確かにBの方が売り上げは上だが、これくらいの差は誤差の範囲ではないだろうか?
これを判断するには確率や統計の知識が必要になってくる。
サイコロと統計
確率を考える上で、まず平均値($\mu$)と分散($\sigma$)を定義しておこう。
\begin{align}
\mu &= \frac{\sum_{i=1}^{N}x_{i}}{N}, \\
\sigma^2&=\frac{\sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2}}{N}
\end{align}
Nは試行回数、$i$番目の試行で出た値を$x_i$とする。
例えばサイコロを100回投げたとすると、N=100となる。
サイコロの確率分布は一定なので、100回投げたとするとだいたい均等に
1-6までの目が出るだろう。
確率分布はこんな感じで一様。
(引用:https://bellcurve.jp/statistics/course/8011.html)
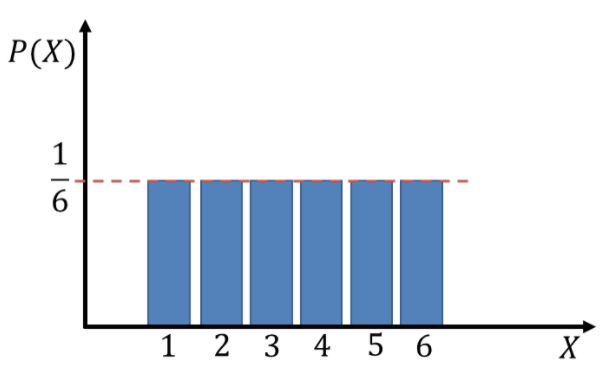
Nが少ないと平均や分散はばらつくが、数を増やしていくと$\mu=3.5$、$\sigma=2.92$あたりに収束する。
では複数回投げた平均値はどうだろうか?
実はサイコロを複数回投げた場合の平均値の分布は一様にはならず、正規分布(ガウス分布)になる。
サイコロの期待値は3.5なので、例えばサイコロを10回投げた平均は大体3.5くらいになるはずだ。
実際には3.4とか3.6とかにばらつくことはあるかもしれないが、10000回とか投げればかなりの精度で
平均値は3.5に収束するだろう。
この平均値の分布の標準偏差を数式で表すと
\frac{\sigma}{\sqrt{N}}\\
となり、これを標準誤差と呼ぶ。
N=1の時は元の分布の標準偏差である$\sigma$と一致し、Nが大きくなるとばらつきは0に近づいていくのでイメージはしやすいと思う。
ここで重要なのが、「もともとの分布は一様分布だったのに、平均値の分布は正規分布になる」ということだ。
以下の図のようにサイコロの数を増やしていくほど、平均値の分布が正規分布に近づいていることがわかる。
画像引用元:https://ai-trend.jp/basic-study/basic/central-limit-theorem/

実はサイコロのような一様分布に限らず、「あらゆる分布の平均値が従う分布は正規分布になる」という性質がある。
これを中心極限定理と呼ぶ。
最初のA/Bテストの例に戻ると、売り上げやCTRなどもともとの分布が正規分布に従っていなかったとしても、ユーザーごとのメトリクス
の平均は正規分布に従うということだ。
これは後々t検定を考える上で重要な性質となる。
正規分布はとても便利
正規分布の数式はこんな感じ。
f(x)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)
分布の期待値が$\mu$、分散が$\sigma^2$だ。
分散は分布の広がりを表し、2乗を取った$\sigma$を標準偏差と呼ぶ。
さらに分かりやすく$\mu=0$、$\sigma^2 = 1$としたものを標準正規分布と呼ぶ。
正規分布にはとても便利な性質がある。
例えば中心から1σの範囲の中に全体の面積の68%が入り、2σの範囲に約95%が収まる。
つまり、正規分布に従うサンプルを何度も発生させた時に、95%は2σより内側の値をとることになる。

引用元:https://ja.wikipedia.org/wiki/%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83
これは検定を行う上でとても便利な性質だ。
例えばサイコロを渡されて、
「本当に1-6まで均等に出るちゃんとしたサイコロかどうか調べてほしい」
と言われたとしよう。
このとき、まず最初に「このサイコロは不具合のない、ちゃんとしたサイコロだ」という仮説を最初に立てる(これ帰無仮説と呼ぶ)。
そして、サイコロを9回降って平均値を求めたとしよう。
サイコロの標準偏差$\sigma$はだいたい1.71くらいなので、この時の標準誤差は先ほどの式から
\frac{1.71}{\sqrt{9}}=0.57
と計算できる。
つまり、サイコロを9回振ったときの平均値の分布は$\mu=3.5, \sigma=0.57$の正規分布に従う。
ここで、サイコロを振って出た目の平均値が4.1だったとしよう。
これは正規分布の1σより内側なので、全体の68%のうちに入っている。
なので、まぁありえそうな値と言える。よって帰無仮説は正しい = ちゃんとしたサイコロと言えそうだ。
逆に、計算値が5.3だったとしよう。
これは分布の3σよりも外側なので、もしサイコロが正常だとしたら0.1%以下の確率でしか出ない値である。
流石にたまたま0.1%を引き当てるなんて考えづらいので、「サイコロは正常だ」という帰無仮説を棄却し、
対立する仮説(対立仮説)である「このサイコロは高い目が出やすい異常なサイコロだ」を受け入れることができるというわけだ。
このようなやり方を仮説検定という。
ちなみにここでは「1σより外側」みたいなざっくりした説明しかしていないが、正規分布の横軸の値がいくつのときに全体の何%になるか(これをp値という)、
が表として存在しているので、これを用いればより詳細にわかる。
https://www.koka.ac.jp/morigiwa/sjs/standard_normal_distribution.htm
RやPythonなどのプログラミングを使えばこれらの値を勝手に計算してくれたりもする。
p値は検定の際のしきい値として用いられる。
よく用いられる値としてp=0.05を使えば、p値が0.05以下の場合に帰無仮説を棄却し対立仮説を受け入れることになる。
A/Bテストにおける検定
さて、しばらく本筋から脱線してしまったので話を元に戻す。
僕たちが知りたいのは今までと同じ青色(A)から赤色(B)に変えるとメトリクスが改善するかどうかだ。
ここで今まで適用してきたAのことをコントロール(Control)、Bのことをテスト(Test) と呼ぼう。(treatmentと呼ぶこともある)
こういったA/Bテストは別名コントロール実験と呼ばれたりする。
そして、Controlに割り当てられたユーザー群をコントロール群、testに割り当てられたユーザー群を介入群と呼ぶ。
これはただの名称なので、あまり気にしなくても大丈夫だ。
コントロール群と介入群でそれぞれメトリクスの平均値を計算することができる。
例えば、ランダム化単位となっているユーザーごとのCTRや収益などだ。
各群でこれらの平均値を求めてやれば、これらは中心極限定理からそれぞれ正規分布に従うはずだ。
コントロール、テストの平均の従う分布の平均を($\mu_{c}, \mu_{t} $)、分散をそれぞれ($\sigma_{Mc}^2, \sigma_{Mt}^2 $)
と表すこととする。
分散については、平均値が従う分布であることを分かりやすくするために$Mt, Mc$と書いている。
実は正規分布に従う変数の差も正規分布になるという性質がある。
テストの平均値からコントロールの平均値を引いた分布を考えると、その平均、分散はそれぞれ
\begin{align}
\mu_{\Delta} &= \mu_t - \mu_c, \\
\sigma_{\Delta}^2&= \sigma_{Mt}^2 + \sigma_{Mc}^2
\end{align}
となる。
元々の分布の分散を$\sigma_t, \sigma_c$とするとこの分散は標準誤差にあたるので
\begin{align}
\sigma_{Mt}&= \frac{\sigma_t}{\sqrt{m}} \\
\sigma_{Mc}&= \frac{\sigma_c}{\sqrt{n}} \\
\end{align}
とも書ける。m, nは介入群、コントロール群それぞれのユーザー数である。
$\mu_{\Delta}, \sigma_{\Delta}$の式に戻ると、
平均値に関してはそのまま引き算になっているが、分散は足し算になっている。
「分散はなんで引き算じゃないの?」と思う人がいるかもしれない。
だが、もし引き算になってしまうと同じ分散を持つ二つの分布の差は分散0で値が確定するような分布になってしまう。
普通に考えて、引く数と引かれる数それぞれにばらつきがあるので、結果のばらつきはその両方を反映したものになっているはずだ。
細かい計算はここでは書かないが、気になった人は調べてみてほしい。
ここで、帰無仮説として
「コントロールとテストの差がない」
と仮定しよう。つまり、文字の色を変えても何も効果がないと仮定する。
すると、上の式において$\mu=0$ということになる。
ここで、正規分布を用いた検定が行える。
つまり、$\mu=0$とした時に、とりうる確率が全体の何%以内に入っているか(つまりp値)を計算する。
そして、p値が0.05より小さければ帰無仮説を棄却し、介入効果(文字色を変えることによる効果)があったとする。
逆にp値が大きければこの介入によって効果があったとは言えないということだ。
ちなみにp値が0.05よりも大きければ95%の区間内に値が収まっていることになり、これを95%の信頼区間と言ったりする。
検定などの複雑な手法を使わなくても単純に信頼区間を誤差棒で表示するやり方もある。
標準正規分布を作る
p値を計算するときには標準正規分布の表を用いたことを思い出そう。
標準正規分布というのは平均が0で分散が1になるような特別な正規分布だ。
今回は帰無仮説において$\mu=0$を考えているので平均値は問題なさそうだが、分散は$\sigma_t^2 + \sigma_c^2$という1でない値をとってしまっている。
どうすれば標準正規分布を作り出せるだろうか?
答えは単純で、全体を分散の値で割ってあげれば良い。
つまり、今までは単純に$\mu_{\Delta} = \mu_t - \mu_c$ の値の分布を見ていたが、これを標準偏差で割って$(\mu_{t} - \mu_c)/\sqrt{\sigma_{Mt}^2 + \sigma_{Mc}^2}$の分布を見ればいい。
これで標準正規分布を用いた検定が行えるはずだ。
これで無事A/Bテストにおける検定が行えるようになった。
ここで計算した$(\mu_t - \mu_c)/\sqrt{\sigma_{Mt}^2 + \sigma_{Mc}^2}$の値をt値と呼ぶ。
なぜt値と呼ぶかはこの後説明する。
t分布とt検定
実はここまで説明した方法には落とし穴がある。
それは標準正規分布を作る際に分布を$(\sigma_{Mt}^2 + \sigma_{Mc}^2)$で割った部分だ。
もしこの値が本来の分布の真の分散を表していれば、確かに割り算した後の分布は標準正規分布になる。
だが、ここで計算した分散はあくまで観測データから計算した分散であり、真の分布の分散からはずれている可能性がある。
もし統計数が十分、つまり各群に十分なユーザー数がいれば確かに分散は真の分散に近づき、標準正規分布になるだろう。
しかしもしユーザー数が不十分であれば、分散は正確に定まらず、分布はより広がった形になるだろう。
実際この分布は標準正規分布にはならず、t分布と呼ばれる分布に従う。

図のようにt分布は正規分布に比べて裾が横に広がったような分布をしているが、自由度$\nu$が大きくなるほど正規分布に近づく。
コントロール群、介入群のユーザー数(メトリクスの計算単位)をそれぞれ$m,n$とすると、この分布は自由度$m+n$の
t分布に従うことがわかっている。
各群のユーザー数が十分大きければ通常の正規分布を使って検定すれば問題ないが、ユーザー数が少ない場合は正規分布を用いて
p値を求めると、正しい値が出ない。
だがこれも心配いらない。
t分布の各自由度ごとにどのt値がどのp値に対応しているかという表がある。
https://www.koka.ac.jp/morigiwa/sjs/td.htm
プログラミングの場合はわざわざ表を用いなくてもt値からp値を勝手に計算してくれたりする。
このようなt値やt分布を使った検定のことをt検定という。
A/Bテストの場合ユーザー数は大きいことが多いので、t検定は実質標準正規分布を使った検定となる。
t分布をもう少し詳しく
さて、t値の式をもう一度見直してみると、以下のように変形できる。
\frac{\mu_t - \mu_c}{\sqrt{\sigma_{Mt}^2 + \sigma_{Mc}^2}}=\frac{\mu_t - \mu_c}{\sqrt{\sigma_{t}^2/m + \sigma_{c}^2/n}}
ここでの$\sigma_t, \sigma_c$は介入(テスト)群とコントロール群でのメトリクスの分散だった。
帰無仮説の元ではもともとのメトリクスの分布は同じはずなので、本来は$\sigma_{t}$も$\sigma_{c}$も同一の値$\sigma$の推定値となるはずだ。この$\sigma$を真の分散とする。
$\sqrt{\sigma_{t}^2/m + \sigma_{c}^2/n}$の部分はもし$\sigma=\sigma_t=\sigma_c$であれば$\sqrt{\sigma^2(1/n+1/m)}$と変形できるはずだ。
この$\sigma$の推定値をSとおくと、
S^2=\frac{1}{m+n-2}(\Sigma_i^m(x_i-\mu_c)^2 + \Sigma_i^n(y_i-\mu_t)^2)
と書ける。
通常の分散の式に似ているが、介入群もコントロール群も同じ分布に従うものとして扱っているので一緒に和を取っている。
$m+n$ではなく$m+n-2$で割っているのは、この値が標本から母集団の分散を見積もる不変推定量だからである。
一般に不変推定量は$S=\frac{\Sigma_i^m(x_i-\mu)^2}{n-1}$のように$n$ではなくn-1で割る。
今回は分布が2つあるので2を引いて$n+m-2$で割っているというわけだ。
従って、t値の式はSを使って
\frac{\mu_t - \mu_c}{\sqrt{S^2(1/n+1/m)}}
となる。
さて、これらを踏まえた上でt値の分子と分母を$\sqrt{\sigma^2(1/n+1/m)}$で割ってみる。
すると上の式の分子は
\frac{\mu_t - \mu_c}{\sqrt{\sigma^2/m + \sigma^2/n}}
となり、$\sigma$は真の値であるためこれは標準正規分布に従う。
一方分母の部分は
\frac{\sqrt{S^2(1/n+1/m)}}{\sqrt{\sigma^2/m + \sigma^2/n}}=\frac{S}{\sigma} \\
= \sqrt{\frac{1}{m+n-2}(\Sigma_i^m(\frac{x_i-\mu_c}{\sigma})^2 + \Sigma_i^n(\frac{y_i-\mu_t}{\sigma})^2)}
となる。
この式を眺めると、標準正規分布に従う変数の和をm+n-1で割った形をしている。
この正規分布に従う変数の和の分布は$\chi$二乗分布と呼ばれる分布だ。($\chi$はカイと読む)
結局のところt分布というのは正規分布をカイ二乗分布で割ったような形をしている。
一般に自由度nのカイ二乗分布の期待値は$n$、分散は$2n$(標準偏差は$\sqrt{2n}$)となる。
これを自由度nで割ると$\mu, \sigma$はそれぞれ1/n倍になるため、期待値が1、標準偏差は$\frac{1}{\sqrt{2n}}$となり、
$n\rightarrow\infty$で分散0で1に収束するため、分子の標準正規分布に収束する。
カイ二乗分布は標準正規分布の2乗和であり、これをnで割るということは標準正規分布の2乗の値が従う分布を用いて
標準誤差を計算しているとも言える。
3つの前提条件を理解する
さて、この後Pythonを用いた具体的な実装についてみていくが、今までの議論では以下の前提をもとにしていたことに気を付けよう。
1. 比較する2つの分布が独立である
今回はA/Bテストを前提としてるため、2つの分布はそれぞれ独立である。
つまり、片方の分布がもう片方に影響することはない。
このような前提でのt検定を「対応なしt検定」と呼ぶ。
実際にはA/Bテストであっても本当の意味で独立であることを担保するのは難しいケースがある。
例えばECサイトの場合だと各ユーザーはおおよそ独立と考えられるが、SNSの場合だと特定ユーザーの変更が口コミなどで他のユーザーに影響する場合がある。
(このケースだとそもそもA/Bテストの設計自体に問題がある可能性もある)
一方で、前後比較のように明確に対応関係があるものには「対応ありt検定」を行う。
例えば特定のサプリメントが効果的かどうかを知りたい場合はサプリメントを飲む前と飲む後での比較となるため「対応あり」となる。
このような場合、一人ひとりがサプリメントを飲む前と後のペアを考え、その差がガウス分布に従うことを仮定したりする。
2. 2群はそれぞれガウス分布に従う
2点目はt検定に使う分布が正規分布に従っていなければならないということだ。
例えばユーザーごとのメトリクス平均値を採用すれば、中心極限定理より正規分布に従うため今回の仮定は成り立つ。
CTRであればユーザーごとのCTRの各群での平均値である。
しかし、売り上げなどの場合は定義上0以上の値しか取らず、高い値に長いtailを引くような分布になっていることが多い。
このような場合はたとえユーザーごとの売り上げ平均を取った場合でもサンプル数が少ないと正規分布には従わないことがあるので注意が必要だ。
この時に必要なサンプル数は分布の左右の偏り(skreness)が大きいほど多くなる。
3. 2群は分散が等しい
前述の帰無仮説の話で$\sigma=\sigma_t=\sigma_c$と置いたことを思い出そう。
ここでは2群の分散は等しいとおいているが、これが本当に成り立っているかも重要だ。
何らかの原因で2群の性質が異なっていたり、母集団の数が異なっている場合はこと仮定が崩れる。
その場合はウィルチのt検定 (Welch's t-test) と呼ばれる手法を用いる必要がある。
ウィルチのt検定においては等分散を仮定していないため、前述のように単純に自由度をn+n-2で割ったりせず、分散の値に応じて調整される。
本筋からそれるため詳しい数式についてはここでは述べない。
SciPyでサクッと計算してみる
Pythonの場合、SciPyのstats.ttest_ind()を使って簡単に計算することができる。
import numpy as np
from scipy import stats
# 2つの標本データを生成(ここでは乱数を使用)
np.random.seed(0) # 乱数生成の再現性を確保
sample1 = np.random.normal(loc=0, scale=1, size=100) # 平均0、標準偏差1の正規分布から100個のデータを生成
sample2 = np.random.normal(loc=0.5, scale=1, size=100) # 平均0.5、標準偏差1の正規分布から100個のデータを生成
# 独立2標本t検定を実行
t_stat, p_value = stats.ttest_ind(sample1, sample2)
print(f"t統計量: {t_stat}, p値: {p_value}")
ここでindは2群が独立な場合のt検定であることを示している。
なお、等分散性を仮定しない場合は以下のようにequal_var=Flaseを設定するだけで簡単にウィルチのt検定を行うことができる。(デフォルトだとTrue)
# ウェルチのt検定を実行
t_stat, p_value = stats.ttest_ind(sample1, sample2, equal_var=False)
まとめ
- コントロール群と介入群のメトリクスの平均値の差が有意がどうかはt検定を用いればよい
- 統計数が多い場合はt検定は実質正規分布を用いた検定となる
- 統計数が少ない場合はt値を用いたt検定を用いればよい
- t分布は標準正規分布をカイ2乗分布で割ったような形をしている
- t検定独立性や等分散性などいくつかの前提条件があるので注意する必要がある
- RやPythonでは簡単にt検定を行うことができる