概要
東京都知事選挙が行われましたが、小池百合子当確(当選確実)の速報がかなり早い段階で出ましたね。
ふと、「当確ってどれくらい開票すればわかるんだろう?」と思ったのでざっくり見積もってみます。
まず最初に知っておきたいのが、当確がわかるまでに必要な票数はどれくらい僅差の勝負かによるということです。圧倒的に票数を獲得している人がいる場合はすぐに確定しそうですし、1位と2位が僅差である場合はいっぱい開票しないとわからないのはなんとなくイメージできると思います。
速報結果をみる
今回は2020年7月5日に行われた都知事選挙を考え1位の小池百合子と2位の宇都宮健児に注目して見ていきます。
では早速速報結果をみていきます。以下のページを参考にしました。
https://www3.nhk.or.jp/news/html/20200705/k10012497581000.html
これをみると、1位の小池百合子が約60%、2位の宇都宮健児が15%ほどに見えますね。
それ以外の候補者はだいたい10%に満たないので今回は考えません。
そもそも当確ってなんだ
そもそも「当確」ってなんだろう?というところから考えていきましょう。
これを決定するためには「誤差」あるいは「信頼区間」を考える必要があります。
例えば全体のうち100票開票して小池百合子が60票だった場合、「だいたい小池百合子が60%くらいだな」ということはわかると思います。
でも、これだけで60%ぴったりと決めてしまうのは危険ですよね。
全部開票したら実は少し多くて62%かもしれないし、59%かもしれない。
だいたい59-61%の間だろうな、と決められるとき、「60%で誤差±1%」と言ったりします。
これは小学校の算数とかでも習う書き方ですね。
一方で統計学の検定という手法を使ったやり方だと
「95%の確率で小池百合子の得票率は59~61%の間にあるだろう」というような言い方をします。
この時に59-61の区間のことを信頼区間と言います。
今回はこれをPythonで実装してみました。
以下の方法で信頼区間○○%の場合、N票開票した結果の得票率がr%だった場合、信頼区間の上限と下限が求まります。
詳しい数式についはとりあえず置いておきますが、だいたいどの統計学の教科書にも載っていて導出可能なので興味のある方は導出してみると統計学の理解が深まると思います。
例えば以下のサイトとかが参考になります:
def getR(r, N):
"""
return: 信頼度x%での得票率の下限と上限, 下限、上限の順で返す
r: 開票結果から計算した得票率
N: 開票した数
信頼区間(x)の決め方
k = 1.96 : 信頼区間95%の場合
k = 2.58 : 信頼区間99%の場合
k = 3.29 : 信頼区間99.9%の場合
"""
k = 3.29 #99.9%
# 下限と上限
lower_limit = r - k * math.sqrt(r*(1-r)/N)
upper_limit = r + k * math.sqrt(r*(1-r)/N)
return lower_limit, upper_limit
matplotlibで可視化してみる
せっかくPythonで関数を定義したので可視化してみましょう。
小池百合子(以下Yuriko)、宇都宮健児(以下Kenji)のだいたいの得票率と信頼区間をplotしてみます。
横軸を開票する票の数として見ていきます。
得票率の平均は開票数によらず小池百合子0.6, 宇都宮健児0.15で固定します。
(本来であればこの値も開票するごとに変化していくはずですが、知るすべがないので...)
まぁでもそんなにずれた結果にはならないはずです。
信頼区間は通常95%のケースで計算することが多いですが、99.9%で計算してみます。
あくまで「当選確実」なので、5%の確率で信頼区間から外れてしまうというのは少し怖いからです。
これを何パーセントにするかは上で定義した関数でkの値を変えれば簡単に変えれます。
ちなみにこのkの値は標準正規分布表というところから引っ張ってきてます。
https://www.koka.ac.jp/morigiwa/sjs/standard_normal_distribution.htm
import numpy as np
import matplotlib.pyplot as plt
import math
# だいたいの得票率
yuriko_rate = 0.6
kenji_rate = 0.15
yuriko_upper = []
yuriko_lower = []
kenji_upper = []
kenji_lower = []
# 100人ずつ1000人まで
N_open = [i for i in range(100,1000, 100)]
for n_open in N_open:
yuriko_lower.append( getR(yuriko_rate, n_open)[0])
yuriko_upper.append( getR(yuriko_rate, n_open)[1])
kenji_lower.append( getR(kenji_rate, n_open) [0])
kenji_upper.append( getR(kenji_rate, n_open) [1])
yuriko_upper = np.array(yuriko_upper)
yuriko_lower = np.array(yuriko_lower)
yuriko_mean = (yuriko_lower + yuriko_upper) / 2
kenji_upper = np.array(kenji_upper)
kenji_lower = np.array(kenji_lower)
kenji_mean = (kenji_lower + kenji_upper) / 2
plt.plot(N_open, yuriko_mean,
color='blue', marker='o',
markersize=5, label='Yuriko')
plt.fill_between(N_open,
yuriko_upper,
yuriko_lower,
alpha=0.15, color='blue')
plt.plot(N_open, kenji_mean,
color='green', linestyle='--',
marker='s', markersize=5,
label='Kenji')
plt.fill_between(N_open,
kenji_upper,
kenji_lower,
alpha=0.15, color='green')
plt.grid()
plt.xlabel('Number of votes')
plt.ylabel('Rates')
plt.legend(loc='upper right')
plt.ylim([0., 1.0])
plt.tight_layout()
plt.show()
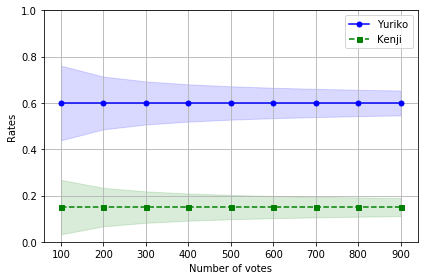
出力結果が以下になります。
信頼区間99.9%とかなり厳しめにしたにも関わらず、わずか100票開票した時点でKenjiの上限よりYurikoの下限のほうが上にありますね。横軸の値が増えるにしたがって精度が上がるためこの区間も収束していきますが、わずかな票数でYurikoが当選確実だということがわかります。
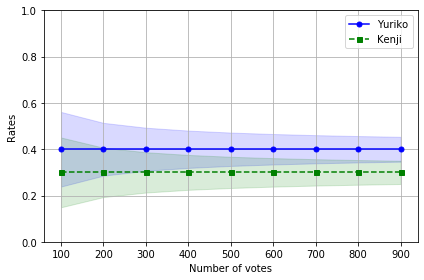
もしYurikoとKenjiがもう少し接戦だった場合はどうなるかも見てみましょう。
今回は速報の時点でYuriko 60%、Kenji 15%とYuriko圧勝でしたが、もう少し僅差だったとしてYurikoが40%、Kenjiが30%だった場合をみてみます。
グラフをみると1000票開票した時でも二人の信頼区間が重なっていますね。
これは1000票開票した結果Yurikoの票数がKenjiより多かったとしても、まだ統計的に十分とは言えないことを示しています。
結論 - 百合子は100票あれば当確 -
今回の都知事選ではかなり早い段階で小池百合子当選確実の報が出たが、1位と2位の得票率の差を考えれば、必要な開票数がかなり少ないことがわかる。
「こんな早くに選挙結果が出るはずがない!不当選挙だ!都民がいったい何人いると思っているんだ!」と言ってる人も世の中にはいたりしますが、そういう人にこそ統計学を勉強してほしいですね。
前にツイッターでみて納得した言い回しが
「味噌汁の味見をするのにすべて飲み干す必要があるかい?」
というものです。だいたい一口味見すれば味噌汁がしょっぱいかどうかなんてわかりますよね?
都民が何人いようと当確の速報を流すのにすべて開票する必要などないのです。
注意点 - データの偏り -
上の計算には一つの重要な仮定が入っています。
それは開票する票に偏りがないということです。
たとえば同じ100票を開票するにしても、「宇都宮健児の地元の票から開票する」とか「20代に絞って開票する」とかいう偏りがあると正しい結果はでません。
偏りを完全になくすことは難しいですが、できるだけ減らすようにランダムに抽出する必要があります。
そういった偏りも考えて実際に当確速報に必要な票数はもう少し多いかもしれませんが、上の図からわかるように100票でも優位な差があるため、どっちにしろそんなに多くの開票は必要ないでしょう。
偏りについても味噌汁の例で説明すると、お湯に味噌をドボンと入れた後にちゃんとかき混ぜないと同じ一口でもすごくしょっぱかったり味がしなかったりするということです。できるだけ混ぜて均一にしてから味見しますよね?
開票と速報もそれと一緒です。
データの偏りの例をいくつか考えてみます。
- 地域差
開票する地域によって支持者は異なるので、少数の票で当確を決定するのであればできるだけランダムに抽出する必要があります。
- 男女差、年代差
同じ投票箱に投票しているのだから年代差や男女差など発生しないはずでは?という疑問もあるかもしれませんが、偏りというのは予期せぬところから発生したりします。例えば、もしかしたら「年配の方が早い時間に投票し、若い人、仕事のある人が遅い時間に投票する」といった投票時間による偏りがある可能性などが考えられます。(あくまで例なので、本当にそうかはわかりませんが)
その場合、早い時間に投票された票から開票した場合に思わぬ偏りが発生する可能性があります。
なお、ここでいう「偏り」というのは選挙で投票された票全体に対する「開票する票」の偏りです。
「今回の選挙は年配の人が多かった」などの母集団全体の性質、偏りとは別だということにも気をつける必要があります。
おまけ - 信頼区間の計算方法 -
少々発展的な内容なので、ここを読み飛ばして最後の追記:乱数を用いたシミュレーションに飛んでもらっても大丈夫です。
上のgetR()で出てきた信頼区間の下限と上限
lower_limit = r - k * math.sqrt(r*(1-r)/N)
upper_limit = r + k * math.sqrt(r*(1-r)/N)
の導出について触れたいと思います。
コードを数式に直します。真の(すべて開票した時の)得票率をRとすると
信頼区間は(下限)< R <(上限)とかけます。つまり
r - k\sqrt{r(1-r)/N}<R<r + k\sqrt{r(1-r)/N}
と書けます。少し変形してみます。
- k\sqrt{r(1-r)/N}< R-r < k\sqrt{r(1-r)/N} \\
- k< \frac{R-r}{\sqrt{r(1-r)/N}} < k
と書けます。この式の意味を考えてみましょう。
「-kからkの間にある」というのは実は意味があります。
このkというのは上でも少し述べたように、標準正規分布表から持ってきたものです。
標準正規分布とは平均値が0、分散(=σ^2)が1の正規分布を表しています。
つまり、このkというのは標準正規分布において信頼区間x%以内に入るのは横軸の値がいくつより内側のときか?というのを計算したものです。
つまり上の式をみると
\frac{R-r}{\sqrt{r(1-r)/N}}
が標準正規分布に従うのだろうな。ということがわかります。
ではこの値が本当に標準正規分布に従うのかを考えていきます。
一般に分散がσ^2、期待値μ、観測値Xの分布があった場合、以下の式は標準正規分布に従います。
\frac{X-\mu}{\sigma}
ちなみに正規分布は左右対称なので、分子は入れ替えても同じです。
こう考えると、R-rのrは途中(N票だけ)開票した時の得票率、Rは真の得票率なのでそのままμ-Xに対応します。
そうすると残りの√r(1-r)/Nの部分はσに対応しそうです。
これも導いてみましょう。
今回のように「開示した票が小池百合子かどうか」という二択を繰り返すことによる分布は二項分布と考えることができます。
一般に二項分布における平均と分散は
\mu = r \\
\sigma^2 = r(1-r)
と表せます。rはある試行において成功する確率です。今回のケースだと「開票した票が小池百合子である確率」にあたります。
今回はこれをN票開票した時の分散を計算します。
一般に平均値の従う分散は(標準誤差)はσ/√Nで計算可能です。従ってこのケースでは
\sqrt{r(1-r)/N}
となり、上の式と一致しましたね。
以上から
\frac{R-r}{\sqrt{r(1-r)/N}}
が標準正規分布に従うことが導け、定義より信頼区間が-k<R<kで計算可能であることがわかりました。
追記:乱数を用いたシミュレーション
上のグラフで一つだけ納得いかなかった点があります。
縦軸にplotした得票率の平均値です。(Yuriko = 0.6, Kenji = 0.15)
上でも少し述べたように、この値は開票するごとに刻々と変化する観測値です。
例えば「10票開票しました!小池百合子5票です!」とか「100票開票しました!小池百合子62票です!」とかそういう値を元に縦軸にplotし、信頼区間で誤差を見積もるのです。
N票開票した時点で誰に何票入っていたかという情報はこちらでは知りようがないので定数として扱っていますが、やや不自然ですね。
なのでこれを乱数を使って簡単にシミュレーションしてみようかと思います。
乱数と言うと難しそうですが、原理は簡単です。
例えば「コインを10回投げて何回表がでるか」といったシミュレーションをしたいとします。
この場合コインで表が出る確率は50%なので、0-1の乱数を10回発生させて、0.5以上が何回出たかを数えれば良いのです。
今回も真の得票率(Yuriko = 0.6, Kenji = 0.15)がわかっていれば以下の関数で計算可能です。
def getMeanRate(R, N):
"""
R : その候補者の真の得票率
N : 開票した票数
p : 0-1の乱数
"""
num = 0 #対象の候補者の票数
for i in range(N):
p = random.random() #0-1の乱数を発生
if(p < R): #開票判定、ドキドキ
num = num + 1 #名前が書いてあったらincrement
return num / N
これを使って縦軸の値をよりリアルにしてみましょう。
上の可視化のコードの前半部分を以下に差し替えます。
# だいたいの得票率
yuriko_rate = 0.6
kenji_rate = 0.15
yuriko_upper = []
yuriko_lower = []
yuriko_mean = [] #追加部分
kenji_upper = []
kenji_lower = []
kenji_mean = [] #追加部分
# 100人ずつ1000人まで
N_open = [i for i in range(100,1000, 100)]
for n_open in N_open:
yuriko_lower.append( getR(yuriko_rate, n_open)[0])
yuriko_upper.append( getR(yuriko_rate, n_open)[1])
yuriko_mean.append( getMeanRate(yuriko_rate, n_open)) #追加部分
kenji_lower.append( getR(kenji_rate, n_open) [0])
kenji_upper.append( getR(kenji_rate, n_open) [1])
kenji_mean.append( getMeanRate(kenji_rate, n_open)) #追加部分
yuriko_upper = np.array(yuriko_upper)
yuriko_lower = np.array(yuriko_lower)
yuriko_mean = np.array(yuriko_mean) #変更部分
kenji_upper = np.array(kenji_upper)
kenji_lower = np.array(kenji_lower)
kenji_mean = np.array(kenji_mean) #変更部分
print(yuriko_mean)
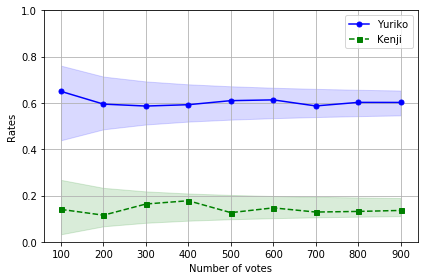
平均値がいい感じにバラついていますね!
信頼区間99.9%なので、プロットした点は全部区間内に収まっています。
これがkの値を少し小さくして95%とかにすると、確率的に20個plotすると1個くらいは信頼区間の外側にはみ出る計算になります。
以上乱数を使った簡単なシミュレーションでした。