はじめに
新しい施策が効果的かどうか知りたいとする。
オンラインでのA/Bテストは最も効果的な方法の一つだ。
どのような施策でテストを行うか、また得られた結果をどのように分析するかは当然大事である。
そしてつい軽視されがちであるが、実験前に必要なサンプル数を見積もるのも同じくらい大事だ。
サンプル数が少なすぎると本来見たい効果が見れないかもしれない。
一方で工数やコスト、リスクの観点からサンプル数をとにかく増やせばいいというものではない。
ここではコンバージョンするかしないか?に絞ったよくあるケースについて、必要なサンプル数を見積もる方法について考えてみよう
おおよその計算式
有意水準5%、検出力80%の場合、A/Bテストに必要なサンプル数nは以下の式で見積もることができる。
(有意水準、検出力の説明については後述)
\begin{aligned}
n&\sim\frac{8({\sigma_T}^2 + {\sigma_C}^2)}{\delta^2}\\
&=\frac{16\sigma^2}{\delta^2}\\
\end{aligned}
$\sigma_C$, $\sigma_{T}$はそれぞれcontrol group、treatment groupの分布の標準偏差である。
実際にはこの二つはおおよそ同じような分布になるので1行目から2行目の変形において$\sigma=\sigma_{C}=\sigma_{T}$と置いている。
ちなみに$σ^2$は分散と呼ばれる。
$\delta$はtreatmentがcontrolを比べてどれくらい精度が上昇したかを表す。
要は$\sigma$と$\delta$の二つが分かれば必要なサンプル数$n$がわかるということだ。
この記事では最終的にこれらの式を導きたい。
卵が先か、鶏が先か
ここまでの話を聞いて「あれ?」と思った人がいるかもしれない。
そもそもA/Bテストにおいてサンプル数nは実験前に決定するものである。
そして実験により「treatmentはcontrolに比べてδ精度が向上しました!」という結果が得られるのである。
実験前のサンプル数の見積もりにδが必要なのは一見矛盾しているように見える。
このδをどのように考えればいいだろうか?
結論から言うと「最低これくらいの改善を計測できるようになりたい」という数値を入れれば良い。
ECサイトを例に考えてみよう。
新しいモデルを導入することにより購入率(CVR)をあげるのが目標としよう。
ビジネス的な観点から、少なくとも5%以上CVRを超えることが見込まれているとする。
そして5%以上CVRが向上すれば新しいモデルを導入し、逆にそれ以下であれは導入は見送るとしよう。
この時、treatmentがcontrolに比べて5%以上の差がある時にちゃんと検出できれば問題ないことになる。
「treatmentがcontrolより0.001%上昇した」として、その差が見えなくても全然問題ないということだ。
ではσはどうだろう?
treatmentの結果は当然A/Bテストを行ったあとしかわからないが、controlであれば実験前に見積もることが可能だ。
例えばユーザーごとに購入に至る確率(つまりConversion Rate)がp(10%)だったとしよう。
この時、ユーザーごとに「買うか買わないか」というp=0.1に従うベルヌーイ試行を考えればいい。
つまり、分布の標準偏差は二項分布で考えることができる。
二項分布において標準偏差は
\sigma=\sqrt{p(1-p)}
で考えることができる。
購入率p=0.1であれば分散は
\sigma^2 = 0.1(1-0.1)=0.09
となる。
ここまで来れば最初の式に代入すれば必要なサンプル数を見積もることができる。
δを仮に0.05と置けば、
n=\frac{16*0.009}{0.0025}=576
つまり必要なサンプル数(今の例ではユーザー数)はだいたい600くらいになる。
n=の式において分母にδがあるため、細かい精度まで見たい場合はδは小さくなり、nは大きくなる。
直感とも合ってそうだ。
帰無仮説
ここで、伝統的な有意差検定において重要な概念である「帰無仮説」を理解しておこう。
これはtreatmentとcontrolに有意な差がないという仮説だ。
この仮説がもし正しければ両者に差はないということになる。
逆にこの仮説が棄却された場合、treatmentとcontrolに有意な差があるということになる。
A/Bテストにおいては帰無仮説が棄却されて初めて「施策に効果がありそう」と見積もることができる。
検出力と有意水準
さて、仮説検定においては帰無仮説が
- 正しいときに、正しく棄却しない選択ができるか
- 正しくないときに、正しく棄却する選択ができるか
が重要となる。
1を間違えるエラーを"Type I Error" (第一種の過誤)と呼ぶ。
これは帰無仮説が正しいにもかかわらず「有意差あり」と判断してしまうケースであり、偽陽性とも言う。
このType I Errorになる確率をαとおこう。
ここで、αは有意水準とも呼ばれる。
例えば、有意水準(α)=5%とは、帰無仮説が正しい場合に間違って棄却してしまう確率が5%以下ということだ。
これは滅多に起こらないため、もしp値がこの値より小さければ帰無仮説を棄却し「有意差あり」と判断する一つの基準になる。
一方で2を間違えるエラーを"Type II Error" (第二種の過誤)と呼ぶ。
これは帰無仮説が正しくないにもかかわらず「有意差なし」と判断してしまうケースであり、偽陰性とも言う。
このType II Errorになる確率をβとおこう。
ここで、1-βは
「帰無仮説が正しくない場合にちゃんと有意差ありと判断できるか?」
を意味し、これを検出力 (Power)と呼ぶ。
このらは後にサンプルサイズを見積もる式の導出で使う。
帰無仮説が正しい場合
さて、帰無仮説が正しい場合、差の従う分布はどうなるだろうか?
具体的に分布をプロットして考えてみよう。
今TreatmentとControlの平均値が従う見たてた2つの標準ガウス分布を発生させ、その差もプロットしてみる。
(平均値が従う分布であるため、元の分布の形に依らず、中心極限定理からガウス分布になる)
PythonでMatplotlibを使ってやってみよう。
ここでは共通の値を使ってみる。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters for two normal distributions
mu1, mu2 = 0, 0
sigma1, sigma2 = 2, 2
x = np.linspace(-10, 10, 1000)
# Calculate PDFs for the control and treatment distributions
y1 = norm.pdf(x, mu1, sigma1)
y2 = norm.pdf(x, mu2, sigma2)
# Calculate the distribution of the difference
diff_stddev = np.sqrt(sigma1**2 + sigma2**2) # Standard deviation of the difference
y_diff = norm.pdf(x, mu2-mu1, diff_stddev)
# Calculate the 95% confidence interval bounds based on the actual distribution
lower_bound_actual, upper_bound_actual = mu2 - mu1 + norm.ppf(0.025) * diff_stddev, mu2 - mu1 + norm.ppf(0.975) * diff_stddev
# Plot Control Distribution
plt.figure(figsize=(8, 3))
plt.plot(x, y1, label=f'Control Distribution\n($\mu$ = {mu1}, $\sigma^2$ = {sigma1**2:.2f})')
plt.title('Control Distribution')
plt.legend(loc='upper left', fontsize='small')
plt.show()
# Plot Treatment Distribution
plt.figure(figsize=(8, 3))
plt.plot(x, y2, label=f'Treatment Distribution\n($\mu$ = {mu2}, $\sigma^2$ = {sigma2**2:.2f})')
plt.title('Treatment Distribution')
plt.legend(loc='upper left', fontsize='small')
plt.show()
# Plot Diff Distribution with confidence interval (using actual distribution, not standardized)
plt.figure(figsize=(8, 3))
plt.plot(x, y_diff, label=f'Diff Distribution\n($\mu$ = 0, $\sigma^2$ = {diff_stddev**2:.2f})')
# Fill the confidence interval area
plt.fill_between(x, y_diff, where=(lower_bound_actual <= x) & (x <= upper_bound_actual), color='skyblue', alpha=0.5, label='95% Confidence Interval')
# Add vertical lines for the confidence interval bounds
plt.axvline(lower_bound_actual, color='r', linestyle='--', label=f'2.5th percentile: {lower_bound_actual:.2f}')
plt.axvline(upper_bound_actual, color='r', linestyle='--', label=f'97.5th percentile: {upper_bound_actual:.2f}')
# Titles and legends
plt.title('Diff Distribution with 95% Confidence Interval')
plt.legend(loc='upper left', fontsize='small')
plt.show()
最初と二番目のグラフはそれぞれctrl/trestに見立てたガウス分布である。
μ、σともに共通の値を使っているため、この二つの分布は同一になる。
今回発生させた分布の分散は"平均値"の従う分布であるため、これらの分散はctrl, treatでそれぞれ標準誤差
$\sigma_C^2/n$, $\sigma_T^2/n$である考えよう。
3つめのグラフは差の従う分布である。
一般に差の従う分布の分散はそれぞれの分散の二乗和で表せるため、
$\frac{\sigma_C^2}{n} + \frac{\sigma_T^2}{n} = \sigma_\Delta^2$
今回のケースでは$\sigma_\Delta$は4+4=8 となる。
やや幅の広い分布になっていることがわかるだろう。
今回は有意水準5%を考え、ガウス分布の両端の裾の割合が2.5%になるように赤い点線が引かれている。
この内側の水色の面積は全体の95%を占めており、この区間を95%の信頼区間と呼ぶ。
もし帰無仮説が正しい場合はほぼ赤線の内側の値を取るはずであり、外側の値を取る確率は5%以下のレアケースである。
レアケースは頻繁には発生しないので、このような値を取ったときに帰無仮説を棄却して「有意差あり」と結論付けたりする。
(もちろん、本当に5%以下のレアケースだった可能性もあり、これがType I Errorにあたる)
$\sigma=1$である標準ガウス分布であればこのラインは
Z_{\alpha/2} = 1.96
くらいになる。
なぜα/2と書いているのかと言えば、ガウス分布の両端が2.5%ずつになっているからである。
もし片側のみを考えるのであれば
Z_{\alpha} = 1.64
の外側を考えれば同じく5%有意水準となる。
今回は分散が1ではないため、実際の分散の値を考えて、赤い線は
Z_{\alpha/2}\sqrt{\frac{\sigma_C^2}{n} + \frac{\sigma_T^2}{n}}
となり、今回の図だと5.54あたりになる。
帰無仮説が正しくない場合
さて、次に帰無仮説が正しくない場合を考えよう。
帰無仮説が正しい場合ではType I Errorを考えたが、正しくない場合はType II Errorについて考える。
ここでも具体的に分布をプロットして考えてみよう。
Treatmentの平均値が従う分布については期待値$\mu$が特定の値(=5)を持つようにする。
# Parameters for two normal distributions
mu1, mu2 = 0, 5 # Treatment mean is now 5
sigma1, sigma2 = 2, 2
x = np.linspace(-10, 15, 1000)
# Calculate PDFs for the control and treatment distributions
y1 = norm.pdf(x, mu1, sigma1)
y2 = norm.pdf(x, mu2, sigma2)
# Calculate the distribution of the difference
diff_stddev = np.sqrt(sigma1**2 + sigma2**2) # Standard deviation of the difference
y_diff = norm.pdf(x, mu2-mu1, diff_stddev)
# Calculate the confidence interval bounds based on the actual distribution
lower_bound_actual, upper_bound_actual = mu2 - mu1 + norm.ppf(0.025) * diff_stddev, mu2 - mu1 + norm.ppf(0.975) * diff_stddev
# Type II Error (False Negative): 80% power, beta = 0.2
# For power = 0.8, we calculate the point where we would fail to reject the null hypothesis
beta_bound = mu2 - mu1 + norm.ppf(0.2) * diff_stddev
# Plot Control Distribution
plt.figure(figsize=(8, 3))
plt.plot(x, y1, label=f'Control Distribution\n($\mu$ = {mu1}, $\sigma^2$ = {sigma1**2:.2f})')
plt.title('Control Distribution')
plt.legend(loc='upper left', fontsize='small')
plt.show()
# Plot Treatment Distribution
plt.figure(figsize=(8, 3))
plt.plot(x, y2, label=f'Treatment Distribution\n($\mu$ = {mu2}, $\sigma^2$ = {sigma2**2:.2f})')
plt.title('Treatment Distribution')
plt.legend(loc='upper left', fontsize='small')
plt.show()
# Plot Diff Distribution with confidence interval and Type II Error region
plt.figure(figsize=(8, 3))
plt.plot(x, y_diff, label=f'Diff Distribution\n($\mu$ = {mu2-mu1}, $\sigma^2$ = {diff_stddev**2:.2f})')
# Highlight Type II Error region (fail to reject null hypothesis despite a real effect)
plt.fill_between(x, y_diff, where=(x > beta_bound), color='lightblue', alpha=0.7)
# Add vertical lines for beta bound
plt.axvline(beta_bound, color='green', linestyle='--', label=f'Power = 80% boundary: {beta_bound:.2f}')
# Titles and legends
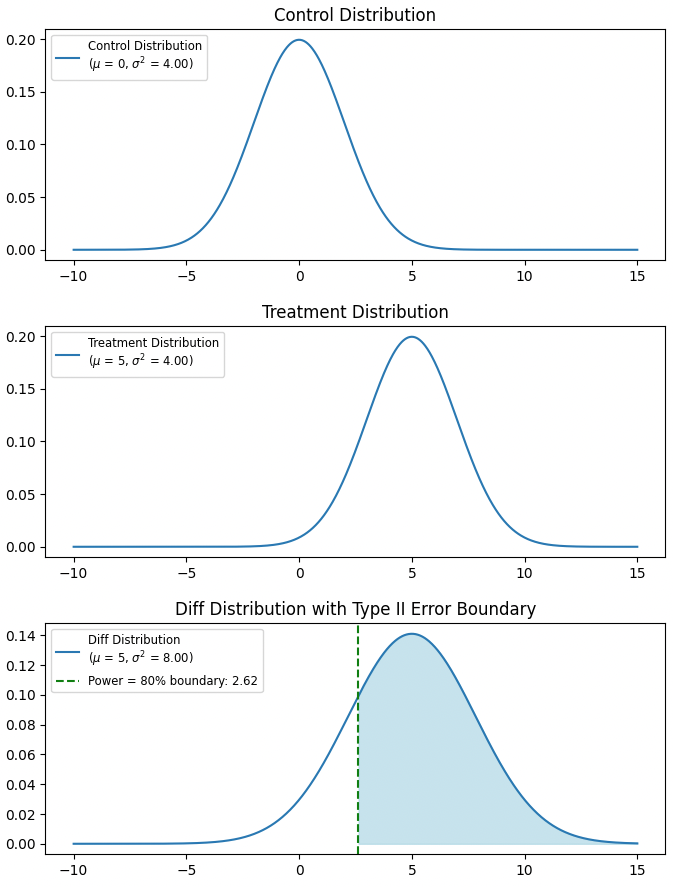
plt.title('Diff Distribution with Type II Error Boundary')
plt.legend(loc='upper left', fontsize='small')
plt.show(
3つ目のグラフは帰無仮説が正しい場合と同じ分散を持つが、期待値μだけがことなることに注目だ。
緑のラインより右側の値が実現したときに「正しく」帰無仮説を棄却できるとしよう。
検出力は80%を満たしたいため、この値は
\mu - Z_{\beta}\sqrt{\frac{\sigma_C^2}{n} + \frac{\sigma_T^2}{n}}
Z_{\beta} = 0.84
となる。
詳細な式を導く
さて、以上の結果を用いていよいよ有意水準α、件出力1-βにおける必要なサンプルサイズの式を導いてみよう。
我々は帰無仮説を仮定して
Z_{\alpha/2}\sqrt{\frac{\sigma_C^2}{n} + \frac{\sigma_T^2}{n}}
よりのラインより大きい値を棄却することで有意水準αを満たせる。
そして本当に有意差があるとき、その差を$\delta$とすると、検出力1-$\beta$を満たすためにはこのラインは
\delta - Z_{\beta}\sqrt{\frac{\sigma_C^2}{n} + \frac{\sigma_T^2}{n}}
である必要がある。
(前述の式の$\mu$を$\delta$とおいた)
従ってこれらを同時に満たすには
\begin{aligned}
Z_{\alpha/2}\sqrt{\frac{\sigma_C^2}{n} + \frac{\sigma_T^2}{n}} &= \delta - Z_{\beta}\sqrt{\frac{\sigma_C^2}{n} + \frac{\sigma_T^2}{n}}\\
\delta &= (Z_{\alpha/2}+Z_{\beta})\sqrt{\frac{\sigma_C^2+\sigma_T^2}{n}}\\
n &= (Z_{\alpha/2}+Z_{\beta})^2 \frac{\sigma_C^2+\sigma_T^2}{\delta^2}
\end{aligned}
となる。
ようやく具体的な形が見えてきた。
ここで
\begin{aligned}
Z_{\alpha/2} = 1.96 \\
Z_{\beta} = 0.84
\end{aligned}
を入れてみると
\begin{aligned}
n &= 7.84 \frac{\sigma_C^2+\sigma_T^2}{\delta^2}\\
& \sim 8 \frac{\sigma_C^2+\sigma_T^2}{\delta^2}
\end{aligned}
となり最初の式が導けた。
最初の式で出てきた8というのはあくまで近似値だったということだ。
また、この式はあくまで
有意水準5%、検出力80%の時に導かれるものであるということに注意が必要だ。
そういう意味では最終系の式を丸暗記するよりも
n = (Z_{\alpha/2}+Z_{\beta})^2 \frac{\sigma_C^2+\sigma_T^2}{\delta^2}
の式から自分で変形しておく方が有効かもしれない。
便利なツール等
以上を踏まえた上で、自分で毎回計算するのは大変なのでツール等を使うと便利だ。
自分は以下のサイトをよく利用している。
各種パラメータを入力すると以下のように必要なサンプルサイズを表示してくれる。

まとめ
- A/Bテストにおいて、よくある条件においてサンプルサイズを求める式を導いた
- より一般的な形の式を覚えておくと、いろんな条件に対応できるかも
- 便利なツールもあるよ
参考文献
- A/Bテスト実践ガイド
-
その他、統計検定準一級、一級関連の書籍やサイト等