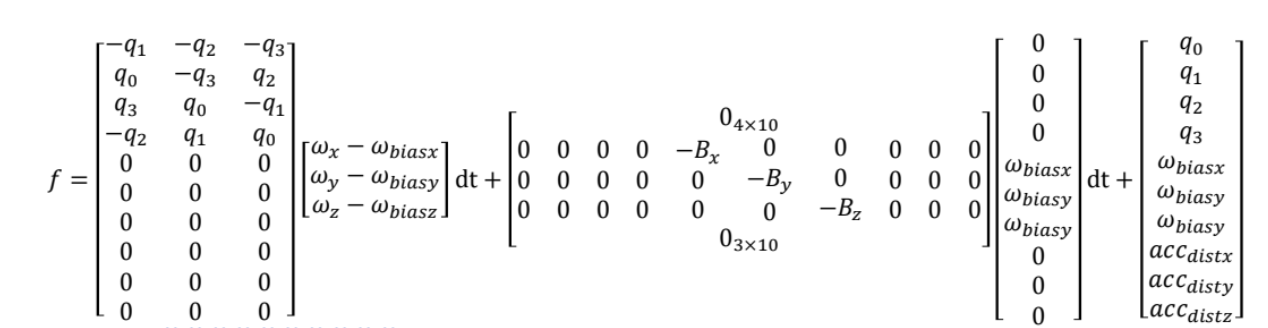はじめに
この記事はABEJA Advent Calendar 2021の2日目の記事です。
こんにちは、ABEJAに2021年新卒で入社した栗林です。1年ほど前にABEJAでエンジニアインターンを経験し、そのときにRaspberry Piの楽しさ・奥深さを知り、それ以来さまざまな工作をしております。この記事の内容は以下の通りです。
- Raspberry Pi zeroを用いた、ドローン用の簡易な姿勢角推定装置を実装する方法をまとめています
- 実際にドローンに搭載するものは500Hz程度での計算が必要になるのでCで実装する必要がありますが、理論の確認ではRaspberry Piでも十分かと思われます。10000円程度で姿勢角推定装置を自作できます!
概要
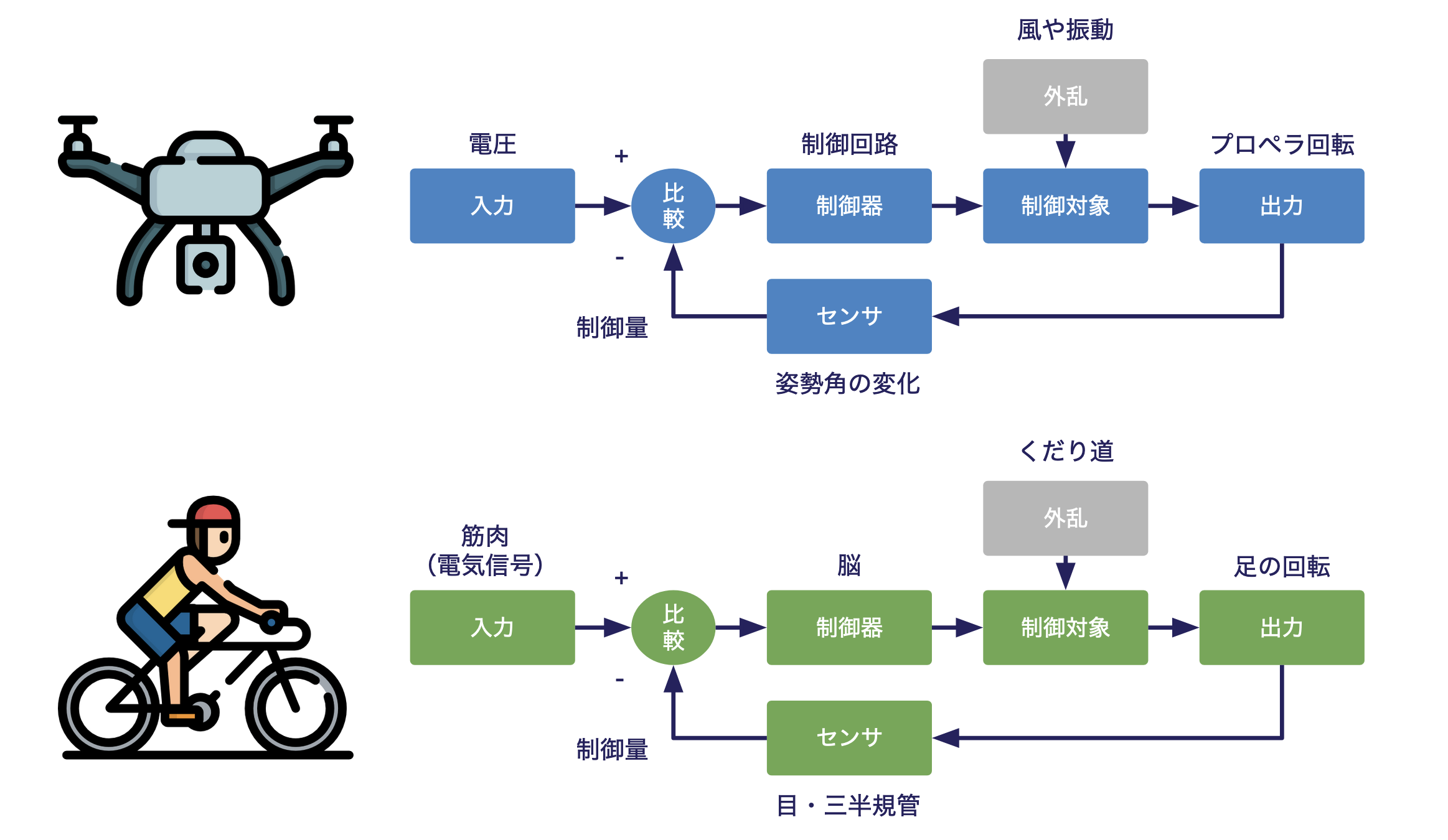
ドローンなどの小型無人航空機(SUAV:Small Unmanned Aerial Vehicle)において、飛行制御を行う際には機体の基本的な状態量を取得することが必要不可欠です。ここでの基本的な状態量とは機体の角度や、速度、位置を指します。もう少し噛み砕いた説明をすると、自転車で直進する際には無意識のうちに次のような動作を行なっているはずです。
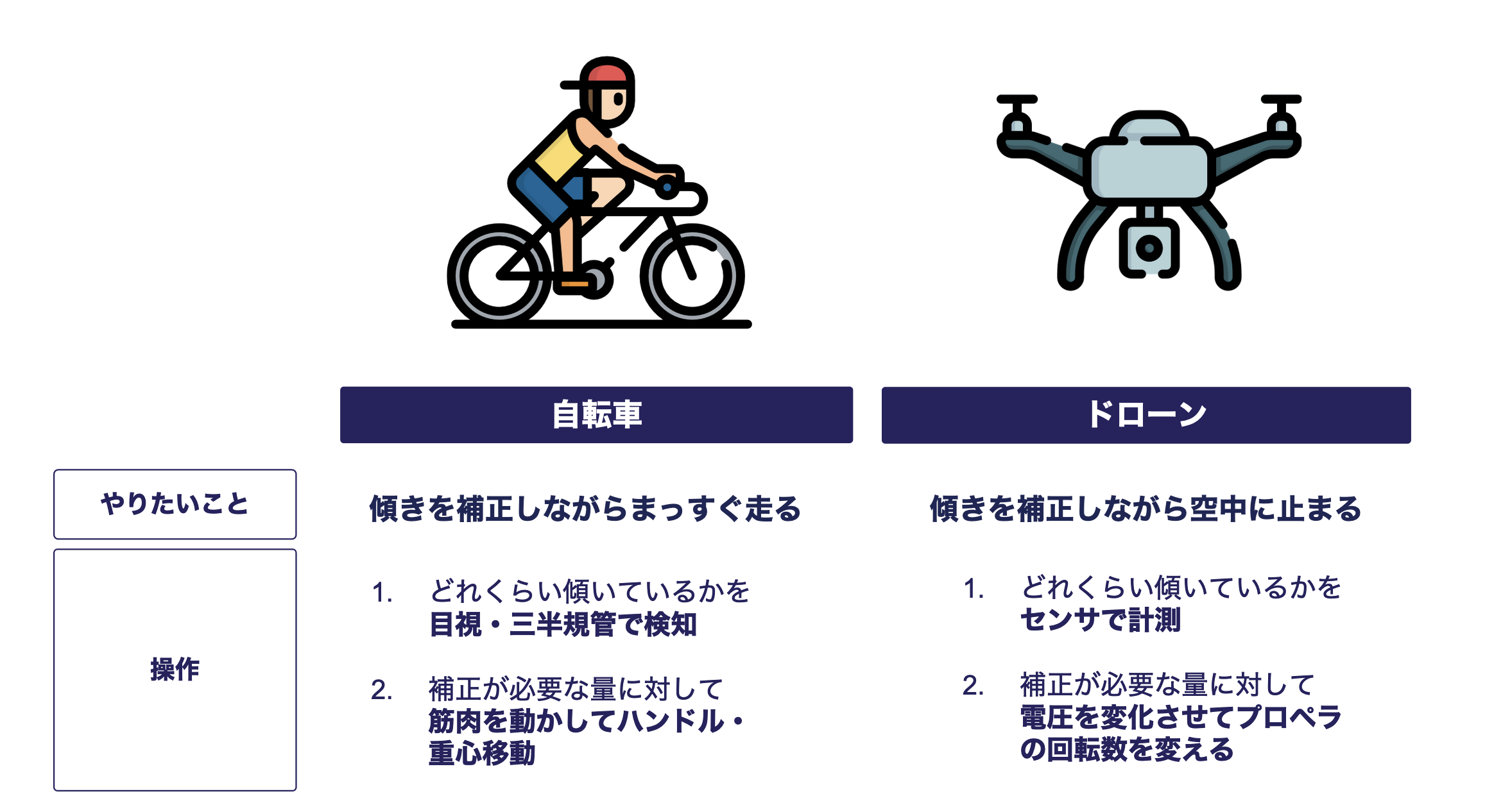
- どれくらい傾いているかを目視・三半規管で検知
- 傾いている補正が必要な量に対して、筋肉を動かしてハンドルや重心を操作
この行程においてわかるのが自転車のハンドル操作(制御)を行うには、自分がどういう状態にあるのかをまず把握する必要があるということです。人間の場合、目視・三半規管によって自己状態の把握を行っていますがSUAVの場合センサで行う必要があります。
一般的には慣性センサと呼ばれる、3cm以下程度の加速度センサや角速度センサが用いられます。そして、これらのセンサを用いて3次元空間における機体の角度(姿勢角)推定を行う、慣性航法システム(INS:Inertial Navigation System)とよばれる技術手法が確立されています。
本日ご紹介するのはこのINSを安価なセンサとRaspberry Piで製作する方法になります!

必要なもの
前提条件の整理
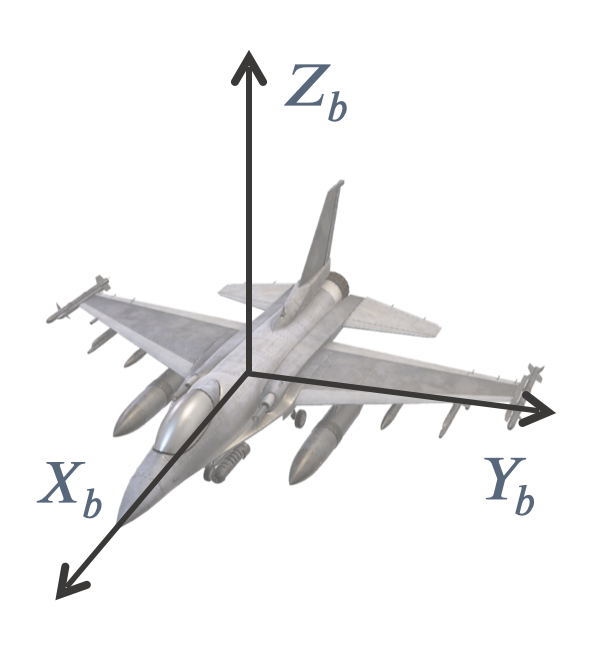
はじめに、何を推定したいかというと機体の姿勢角です。姿勢角とは地上座標から見た時の機体の3軸方向の角度です(一部の表現を省略しています)。静止状態においては以下のような方法で推定することが可能です。
- 加速度センサと磁気センサを使用
各軸方向に発生する重力加速度の大きさを計測し、垂線からの傾きを把握。その傾きと磁気センサを考慮することで方位を決定。
ただし、実際には機体は運動を行うため重力加速度に加えて運動時の加速度が印加されます。これを取り除く必要がありますがどのようにしたらよいでしょうか?答えのひとつは角速度センサを用いることです。時間ごとの角度変化量情報を加えることで、運動によって発生した加速度の大きさを推定します。
理論
上記までの内容を数式で説明します。
カルマンフィルタ
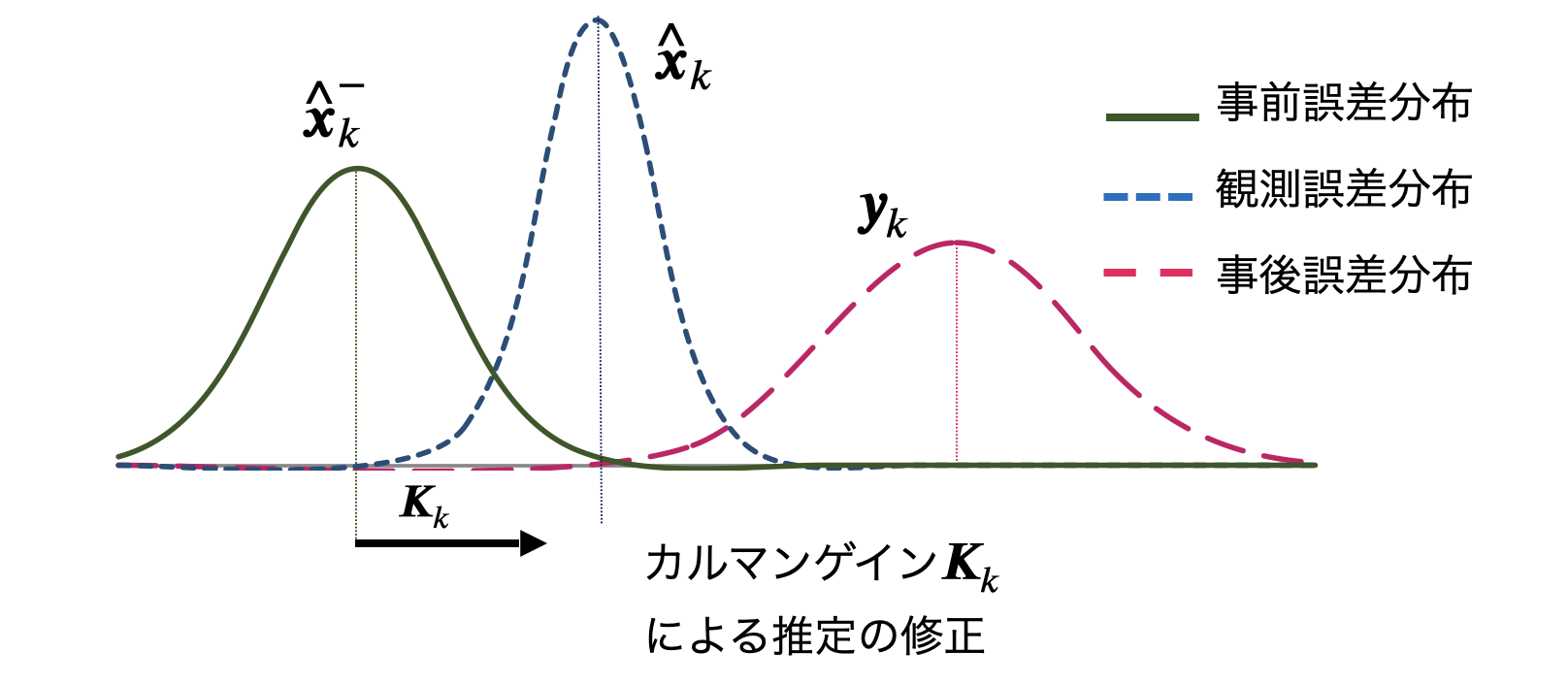
センサから取得された過去・現在の値を利用して、最も確からしい値を推定するために拡張カルマンフィルタを用います。カルマンフィルタについての基本的な説明はこちらの記事( https://qiita.com/IshitaTakeshi/items/740ac7e9b549eee4cc04 )などがおすすめです。
INSでは非線形システムを対象とするため、システム各時間において線形化された時変のカルマンフィルタを適用します。事前誤差分布が前ステップまでに計算ができており、現ステップにおいて新たな観測値および観測(センサ値)誤差分布が取得できた際に次ステップの誤差分布を計算します。
離散時間状態方程式および、観測方程式は次式で表されます。
状態遷移行列、観測行列をテイラー級数展開を用いて線形近似します。

時間更新式 k=0, 1, 2, ... Nに対して次式を計算します。
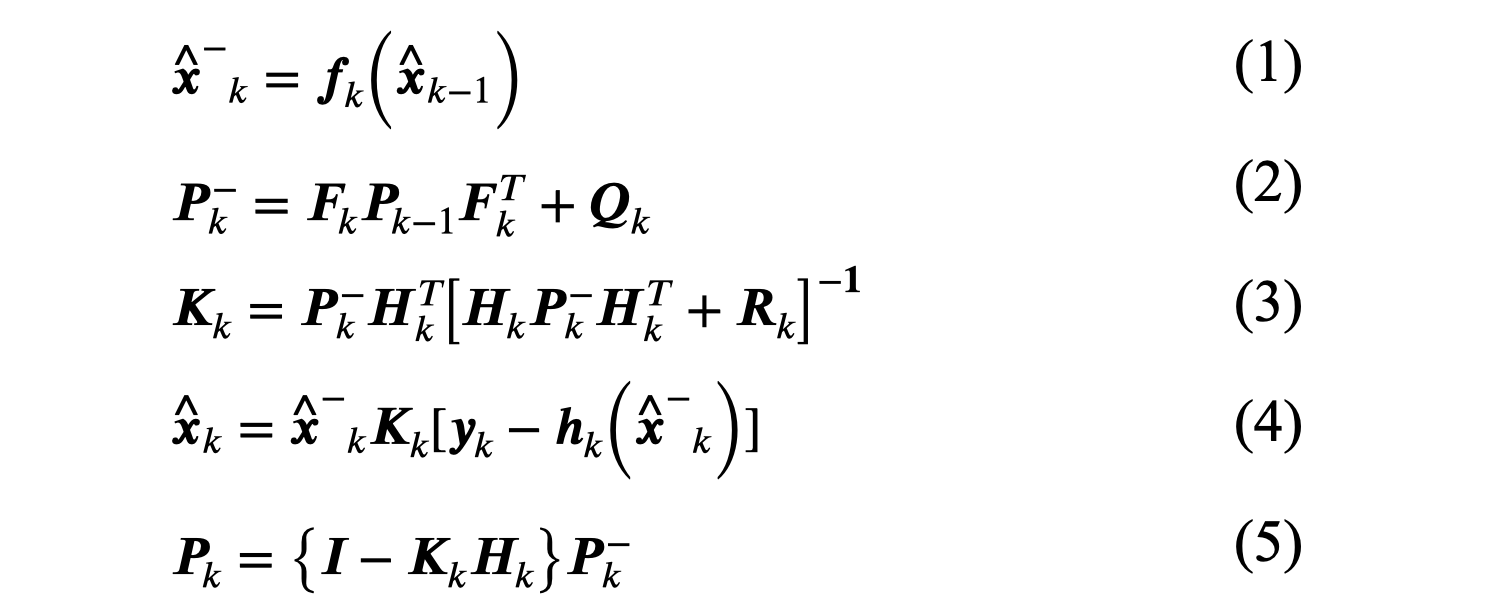
次に状態方程式についてです。ここで姿勢角表現にクオータニオンを用います。クオータニオンの導入理由としては計算特異点がないこと、計算速度が早いことが挙げられます(くわしくはこちらをご参照ください:https://qiita.com/drken/items/0639cf34cce14e8d58a5 )。

実装
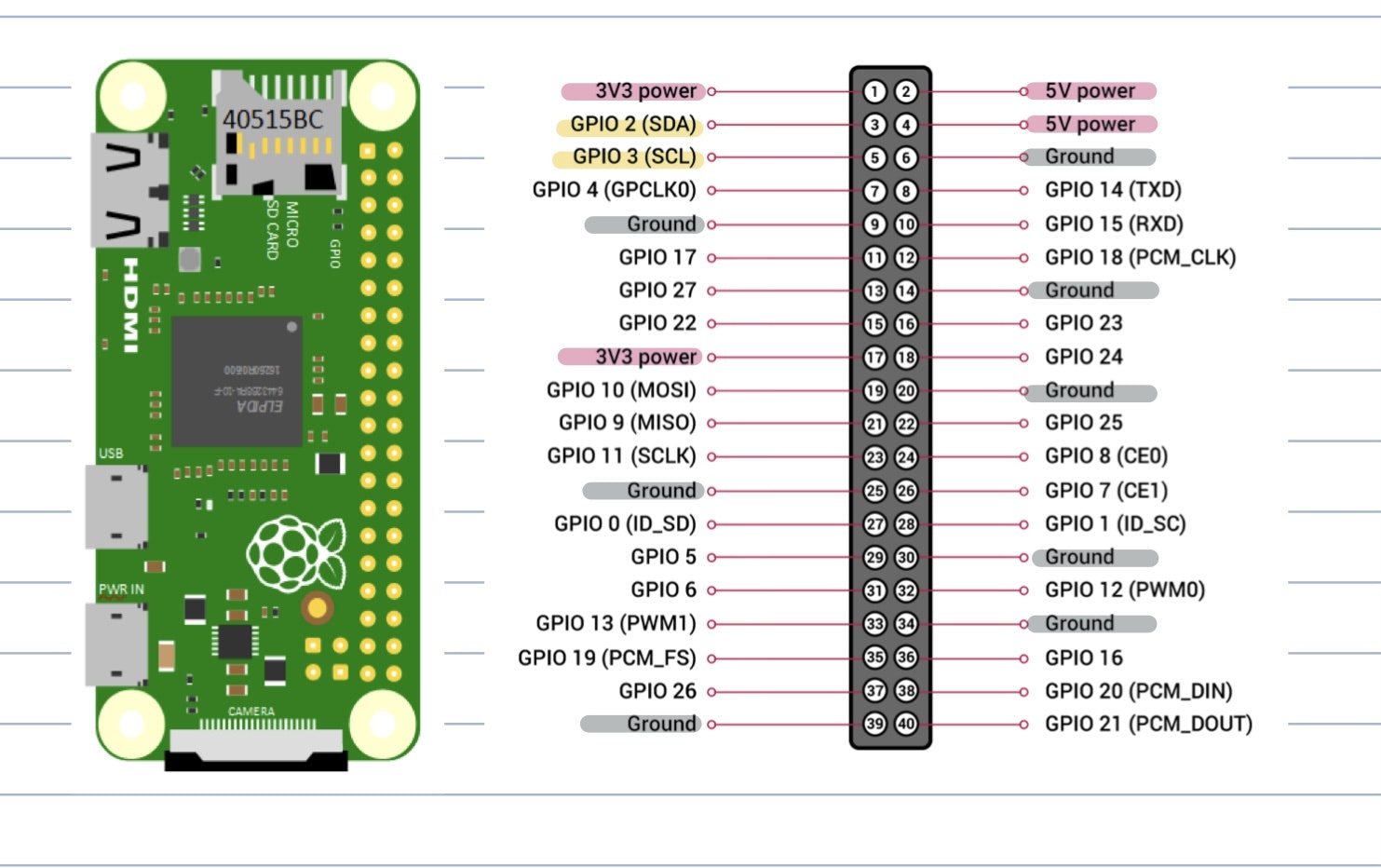
Raspberry Pi zeroおよびセンサのセッティング
簡単に整理すると以下の順で姿勢角の計算が行われます。
- y :センサによる観測値の取得・更新
- f,F :状態遷移行列の計算および線形近似
- h,H :変換行列の計算および線形近似
- K :カルマンフィルタ(カルマンゲイン)計算
- Ang :姿勢角推定
- Pb :次ステップでの計算に使われる、事後共分散行列計算
ですので、一番はじめの観測値を取得するためにセンサとの連携を設定します。
Raspberry Piによるセンサデータ取得
基本的にはI2C通信を利用して接続するだけです。
こちらの記事を参考にさせていただきました。
https://asukiaaa.blogspot.com/2018/04/raspberry-pi-mpu9250.html
class UART:
def __init__(self):
# シリアル通信設定
# ボーレートはラズパイのデフォルト値:115200に設定
try:
self.uartport = serial.Serial(
port="/dev/ttyS0",
baudrate=115200,
bytesize=serial.EIGHTBITS,
parity=serial.PARITY_NONE,
stopbits=serial.STOPBITS_ONE,
timeout=None,
)
except serial.SerialException:
print(traceback.format_exc())
# 受信バッファ、送信バッファクリア
self.uartport.reset_input_buffer()
self.uartport.reset_output_buffer()
time.sleep(0.5)
def send_serial(self, cmd):
print("send data : {0}".format(cmd))
try:
# 改行コードを必ずつけるために、1回削除して、送信時に再度付与する
cmd = cmd.rstrip()
# 改行コードを付与 文字列をバイナリに変換して送信
self.uartport.write((cmd + "\n").encode("utf-8"))
except serial.SerialException:
print(traceback.format_exc())
def receive_serial(self):
"""UART受信関数
シリアルポートで受信したcharデータを1行読み取り文字コードutf-8に変換.dataとして返す.
Args:
-
Returns:
data: char型,1行分の文字列
"""
try:
rcvdata = self.uartport.readline()
except serial.SerialException:
print(traceback.format_exc())
try:
# 受信したバイナリデータを文字列に変換 改行コードを削除
return rcvdata.decode("utf-8").rstrip()
except UnicodeDecodeError:
print("unicode decode error. wait a second")
def raw_data(self,data):
"""受信データをそのまま数値として出力する
UART受信データにオフセット,係数倍をせず出力する.キャリブレーション用.
Args:
data: char型. シリアル通信による1行の文字データ
Returns:
sens[0]: float. MAVC3の時間カウント
sens_raw: floatリスト.各センサごとの数値データ.
"""
try:
received_data = data.split(',')
sens_raw = [0]*11
#char型をfloat型に変換
if received_data[0]=="Tms":
sens_raw[0] = float(received_data[1])
if received_data[2]=="Acc":
sens_raw[1] = float(received_data[3])
sens_raw[2] = float(received_data[4])
sens_raw[3] = float(received_data[5])
if received_data[6]=="Gyr":
sens_raw[4] = float(received_data[7])
sens_raw[5] = float(received_data[8])
sens_raw[6] = float(received_data[9])
if received_data[10]=="Mag":
sens_raw[7] = float(received_data[11])
sens_raw[8] = float(received_data[12])
sens_raw[9] = float(received_data[13])
sens_raw[10] = received_data[14]
except ValueError:
print("data isn't correct: ValueError")
except IndexError:
print("data isn't correct: IndexError")
except AttributeError:
print("nonetype object has no attribute 'split': AttributeError")
return sens_raw[0],sens_raw
上記で取得されたセンサーの値(sens_raw)を状態遷移行列に観測値(y_obs)として与え計算します。
# 初期値例等
xa = np.zeros(M_x)
xb = np.zeros(M_x)
xb_norm = np.zeros(4)
xa_norm = np.zeros(4)
xa_temp_1 = np.zeros(M_y)
xa_temp_2 = np.zeros(M_x)
# ノイズのパラメータ
Bx = 0.5
By = 0.5
Bz = 0.5
f = np.zeros(M_x)
P = np.identity(M_x)*0.01
Pa = np.identity(M_x)*0.01
Pb = np.zeros((M_x,M_x))
eyeF = np.identity(M_x) #Fと同じ行列サイズの単位行列
y_before = np.zeros(Y)
y_obs_raw = np.zeros(Y)
y_obs = np.zeros(Y)
# 角速度バイアス,加速度外乱初期値
w_bias_init = np.array([0.001,0.001,0.001])
a_dist_init = np.array([0.0,0.0,0.0])
q_init = np.array([1,0,0,0])
F = np.zeros((M_x,M_x))
F_tran = np.zeros((M_x,M_x))
G = np.array([[0,0,0],
[0,0,0],
[0,0,0],
[0,0,0],
[dt,0,0],
[0,dt,0],
[0,0,dt],
[0,0,0],
[0,0,0],
[0,0,0]])
G_tran = np.zeros((3,M_x))
Qn = np.array([[Qn_var,0,0],
[0,Qn_var,0],
[0,0,Qn_var]])
Rn = np.array([[Rn_var_1,0,0,0,0,0],
[0,Rn_var_1,0,0,0,0],
[0,0,Rn_var_1,0,0,0],
[0,0,0, Rn_var_2,0,0],
[0,0,0, 0,Rn_var_2,0],
[0,0,0, 0,0,Rn_var_2]])
Rot_Q = np.zeros(9)
Rot_R = np.zeros(9)
h = np.zeros(M_y)
Q_dot_1 = np.zeros((3,M_x))
Q_dot_2 = np.zeros((3,M_x))
Q_dot_3 = np.zeros((3,M_x))
# H行列算出のため
H = np.zeros((M_y,M_x))
H_g_z = np.zeros((3,M_x))
H_dist_x = np.zeros((3,M_x))
H_dist_y = np.zeros((3,M_x))
H_dist_z = np.zeros((3,M_x))
H_mag_x = np.zeros((3,M_x))
H_mag_y = np.zeros((3,M_x))
H_mag_z = np.zeros((3,M_x))
H_acc = np.zeros((3,M_x))
H_mag = np.zeros((3,M_x))
H_tran = np.zeros((M_x,M_y))
K_temp = np.zeros((M_x,M_x))
K_temp_inv = np.zeros((M_x,M_x))
ang_temp = np.zeros(3)
ang = np.zeros(3)
# 状態遷移行列
F = np.array([
[1, -0.5*(y_obs[3]-xb[4])*dt, -0.5*(y_obs[4]-xb[5])*dt, -0.5*(y_obs[5]-xb[6])*dt, 0.5*xb[1]*dt, 0.5*xb[2]*dt, 0.5*xb[3]*dt, 0, 0, 0],
[0.5*(y_obs[3]-xb[4])*dt, 1, 0.5*(y_obs[5]-xb[6])*dt, -0.5*(y_obs[4]-xb[5])*dt, -0.5*xb[0]*dt, 0.5*xb[3]*dt, -0.5*xb[2]*dt, 0, 0, 0],
[0.5*(y_obs[4]-xb[5])*dt, -0.5*(y_obs[5]-xb[6])*dt, 1, 0.5*(y_obs[3]-xb[4])*dt, -0.5*xb[3]*dt, -0.5*xb[0]*dt, 0.5*xb[1]*dt, 0, 0, 0],
[0.5*(y_obs[5]-xb[6])*dt, 0.5*(y_obs[4]-xb[5])*dt, -0.5*(y_obs[3]-xb[4])*dt, 1, 0.5*xb[2]*dt, -0.5*xb[1]*dt, -0.5*xb[0]*dt, 0, 0, 0],
[0, 0, 0, 0, 1-Bx*dt, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 1-By*dt, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1-Bz*dt, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
])
機体軸および、地上軸での加速度や地磁気を変換する行列の計算です。
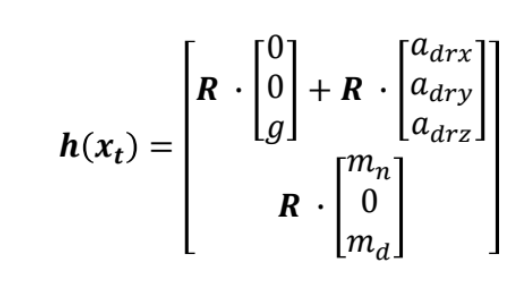
# 変換行列
h = np.array([
Rot_Q[2]*g + Rot_Q[0]*xb[7] + Rot_Q[1]*xb[8] + Rot_Q[2]*xb[9],
Rot_Q[5]*g + Rot_Q[3]*xb[7] + Rot_Q[4]*xb[8] + Rot_Q[5]*xb[9],
Rot_Q[8]*g + Rot_Q[6]*xb[7] + Rot_Q[7]*xb[8] + Rot_Q[8]*xb[9],
Rot_Q[0]*m_x + Rot_Q[1]*m_y + Rot_Q[2]*m_z,
Rot_Q[3]*m_x + Rot_Q[4]*m_y + Rot_Q[5]*m_z,
Rot_Q[6]*m_x + Rot_Q[7]*m_y + Rot_Q[8]*m_z
])
カルマンフィルタ計算時に必要になる転置行列を事前に計算します
# 転置行列計算
F_tran = F.T
G_tran = G.T
H_tran = H.T
# 事前共分散行列 Pb (10*10)
Pb = (F @ P) @ F_tran + (G @ Qn) @ G_tran
# カルマンゲイン K (10*6)
# 事前に分母を計算,逆行列にする
K_temp = H @ Pb @ H_tran + Rn
K_temp_inv = np.linalg.inv(K_temp)
K = (Pb @ H_tran) @ K_temp_inv
計算したカルマンゲインから推定を行い、クオータニオンを姿勢角に変換します。
# クオータニオンの正規化
for k in range(4):
xa_norm[k] = xa_temp_2[k]/math.sqrt(xa_temp_2[0]*xa_temp_2[0]+xa_temp_2[1]*xa_temp_2[1]+xa_temp_2[2]*xa_temp_2[2]+xa_temp_2[3]*xa_temp_2[3])
xa[0] = xa_norm[0]
xa[1] = xa_norm[1]
xa[2] = xa_norm[2]
xa[3] = xa_norm[3]
xa[4] = xa_temp_2[4]
xa[5] = xa_temp_2[5]
xa[6] = xa_temp_2[6]
xa[7] = xa_temp_2[7]
xa[8] = xa_temp_2[8]
xa[9] = xa_temp_2[9]
以上の観測値取得から推定までの処理をまとめると以下のようになります。
def calc_kalmanfilter(self):
global main_count
if main_count==0:
ins.kf_init()
for j in range(Y):
y_before[j] = y_obs_raw[j]
main_count = 1
else:
#初回以降,前回のデータと併せて平滑化を適用
ratio = 0.5
for j in range(Y):
y_obs[j] = ratio*y_obs_raw[j] + (1-ratio)*y_before[j]
#現ステップの観測値を1ステップ前の観測値として保存
y_before[j] = y_obs[j]
f =[
(-0.5*dt*xa[1]*(y_obs[3]-xa[4]) - 0.5*dt*xa[2]*(y_obs[4]-xa[5]) -0.5*dt*xa[3]*(y_obs[5]-xa[6]) + xa[0]),
(0.5*dt*(xa[0])*(y_obs[3]-xa[4]) - 0.5*dt*xa[3]*(y_obs[4]-xa[5]) +0.5*dt*(xa[2])*(y_obs[5]-xa[6]) + xa[1]),
(0.5*dt*(xa[3])*(y_obs[3]-xa[4]) + 0.5*dt*(xa[0])*(y_obs[4]-xa[5]) - 0.5*dt*xa[1]*(y_obs[5]-xa[6]) + xa[2]),
(-0.5*dt*xa[2]*(y_obs[3]-xa[4]) + 0.5*dt*(xa[1])*(y_obs[4]-xa[5]) + 0.5*dt*(xa[0])*(y_obs[5]-xa[6]) + xa[3]),
xa[4]*(1-Bx*dt),
xa[5]*(1-By*dt),
xa[6]*(1-Bz*dt),
xa[7],
xa[8],
xa[9]
]
#クオータニオンの正規化
for k in range(4):
xb_norm[k] = f[k]/math.sqrt(f[0]*f[0]+f[1]*f[1]+f[2]*f[2]+f[3]*f[3])
#正規化したクオータニオンの値を事前推定値xbに代入
xb[0] = xb_norm[0]
xb[1] = xb_norm[1]
xb[2] = xb_norm[2]
xb[3] = xb_norm[3]
xb[4] = f[4]#w_bias_x 推定値
xb[5] = f[5]
xb[6] = f[6]
xb[7] = f[7]#a_disturbance_x 推定値
xb[8] = f[8]
xb[9] = f[9]
F = np.array([
[1, -0.5*(y_obs[3]-xb[4])*dt, -0.5*(y_obs[4]-xb[5])*dt, -0.5*(y_obs[5]-xb[6])*dt, 0.5*xb[1]*dt, 0.5*xb[2]*dt, 0.5*xb[3]*dt, 0, 0, 0],
[0.5*(y_obs[3]-xb[4])*dt, 1, 0.5*(y_obs[5]-xb[6])*dt, -0.5*(y_obs[4]-xb[5])*dt, -0.5*xb[0]*dt, 0.5*xb[3]*dt, -0.5*xb[2]*dt, 0, 0, 0],
[0.5*(y_obs[4]-xb[5])*dt, -0.5*(y_obs[5]-xb[6])*dt, 1, 0.5*(y_obs[3]-xb[4])*dt, -0.5*xb[3]*dt, -0.5*xb[0]*dt, 0.5*xb[1]*dt, 0, 0, 0],
[0.5*(y_obs[5]-xb[6])*dt, 0.5*(y_obs[4]-xb[5])*dt, -0.5*(y_obs[3]-xb[4])*dt, 1, 0.5*xb[2]*dt, -0.5*xb[1]*dt, -0.5*xb[0]*dt, 0, 0, 0],
[0, 0, 0, 0, 1-Bx*dt, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 1-By*dt, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1-Bz*dt, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
])
#変換行列hを定義する
#回転行列準備:計算簡略化のためクオータニオンの回転行列を以下のように定義
#Rot_Q = [Rot_Q[0] Rot_Q[1] Rot_Q[2]
# Rot_Q[3] Rot_Q[4] Rot_Q[5]
# Rot_Q[6] Rot_Q[7] Rot_Q[8]]
Rot_Q[0] = xb[0]*xb[0] + xb[1]*xb[1] - xb[2]*xb[2] - xb[3]*xb[3]
Rot_Q[1] = 2*(xb[1]*xb[2] + xb[0]*xb[3])
Rot_Q[2] = 2*(xb[3]*xb[1] - xb[2]*xb[0])
Rot_Q[3] = 2*(xb[1]*xb[2] - xb[3]*xb[0])
Rot_Q[4] = xb[0]*xb[0] - xb[1]*xb[1] + xb[2]*xb[2] - xb[3]*xb[3]
Rot_Q[5] = 2*(xb[2]*xb[3] + xb[1]*xb[0])
Rot_Q[6] = 2*(xb[3]*xb[1] + xb[2]*xb[0])
Rot_Q[7] = 2*(xb[2]*xb[3] - xb[1]*xb[0])
Rot_Q[8] = xb[0]*xb[0] - xb[2]*xb[2] + xb[3]*xb[3] - xb[1]*xb[1]
h = np.array([
Rot_Q[2]*g + Rot_Q[0]*xb[7] + Rot_Q[1]*xb[8] + Rot_Q[2]*xb[9],
Rot_Q[5]*g + Rot_Q[3]*xb[7] + Rot_Q[4]*xb[8] + Rot_Q[5]*xb[9],
Rot_Q[8]*g + Rot_Q[6]*xb[7] + Rot_Q[7]*xb[8] + Rot_Q[8]*xb[9],
Rot_Q[0]*m_x + Rot_Q[1]*m_y + Rot_Q[2]*m_z,
Rot_Q[3]*m_x + Rot_Q[4]*m_y + Rot_Q[5]*m_z,
Rot_Q[6]*m_x + Rot_Q[7]*m_y + Rot_Q[8]*m_z
])
#H行列の計算
#計算準備 回転行列の各成分を偏微分
Q_dot_1 = np.array([
[xb[0], -xb[1], -xb[2], xb[3], 0, 0, 0, 0, 0, 0],
[-xb[3], xb[2], xb[1], -xb[0], 0, 0, 0, 0, 0, 0],
[xb[2], xb[3], xb[0], xb[1], 0, 0, 0, 0, 0, 0]
])
Q_dot_2 = np.array([
[xb[3], xb[2], xb[1], xb[0], 0, 0, 0, 0, 0, 0],
[xb[0], -xb[1], xb[2], -xb[3], 0, 0, 0, 0, 0, 0],
[-xb[1], -xb[0], xb[3], xb[2], 0, 0, 0, 0, 0, 0]
])
Q_dot_3 = np.array([
[-xb[2], xb[3], -xb[0], xb[1], 0, 0, 0, 0, 0, 0],
[xb[1], xb[0], xb[3], xb[2], 0, 0, 0, 0, 0, 0],
[xb[0], -xb[1], -xb[2], xb[3], 0, 0, 0, 0, 0, 0]
])
#H = {H_acc: H_mag}となる
for k in range(3):
for l in range(M_x):
#----------------------------------
#acc,加速度
#加速度成分:重力加速度
# x 方向は重力加速度なし Q_dot_1
# y 方向は重力加速度なし Q_dot_2
H_g_z[k][l] = 2*g*Q_dot_3[k][l]
#加速度成分:外乱
H_dist_x[k][l] = 2*xb[7]*Q_dot_1[k][l]
H_dist_y[k][l] = 2*xb[8]*Q_dot_2[k][l]
H_dist_z[k][l] = 2*xb[9]*Q_dot_3[k][l]
#----------------------------------
#mag,地磁気
#地磁気成分
H_mag_x[k][l] = 2*m_x*Q_dot_1[k][l]
H_mag_y[k][l] = 2*m_y*Q_dot_2[k][l]
H_mag_z[k][l] = 2*m_z*Q_dot_3[k][l]
#----------------------------------
#H = {H_acc: H_mag}となるように加算
H_acc = H_g_z + H_dist_x + H_dist_y + H_dist_z
H_mag = H_mag_x + H_mag_y + H_mag_z
H = np.concatenate([H_acc, H_mag]) #縦方向に行列を結合
#転置行列計算 F', G', H' (')= (_tran)
F_tran = F.T
G_tran = G.T
H_tran = H.T
#事前共分散行列 Pb (10*10) = F*P*F' + G*Qn*G'
Pb = (F @ P) @ F_tran + (G @ Qn) @ G_tran
#カルマンゲイン K (10*6) = Pb*H'/H*Pb*H'+Rn
#Pb(10*10)*H'(10*6)/H(6*10)*Pb(10*10)*H'(10*6)+Rn(6*6)
#事前に分母を計算,逆行列にする
K_temp = H @ Pb @ H_tran + Rn
K_temp_inv = np.linalg.inv(K_temp)
K = (Pb @ H_tran) @ K_temp_inv
#事後推定値 xa (10*1) = xb+K*(y-h)
#加速度観測値
xa_temp_1[0] = y_obs[0] - h[0]
xa_temp_1[1] = y_obs[1] - h[1]
xa_temp_1[2] = y_obs[2] - h[2]
#地磁気観測値
xa_temp_1[3] = y_obs[6] - h[3]
xa_temp_1[4] = y_obs[7] - h[4]
xa_temp_1[5] = y_obs[8] - h[5]
#xb[0] + K@(y[0]-h[0])
xa_temp_2 = xb + K @ xa_temp_1
#クオータニオンの正規化
for k in range(4):
xa_norm[k] = xa_temp_2[k]/math.sqrt(xa_temp_2[0]*xa_temp_2[0]+xa_temp_2[1]*xa_temp_2[1]+xa_temp_2[2]*xa_temp_2[2]+xa_temp_2[3]*xa_temp_2[3])
xa[0] = xa_norm[0]
xa[1] = xa_norm[1]
xa[2] = xa_norm[2]
xa[3] = xa_norm[3]
xa[4] = xa_temp_2[4]
xa[5] = xa_temp_2[5]
xa[6] = xa_temp_2[6]
xa[7] = xa_temp_2[7]
xa[8] = xa_temp_2[8]
xa[9] = xa_temp_2[9]
#事後共分散行列計算
#Pa = eye(10*10) - K*H*Pb
Pa = (eyeF - K @ H) @ Pb
#推定値の更新
#次ステップの事前共分散行列は今回の事後共分散行列
for k in range(M_x):
for l in range(M_x):
P[k][l] = Pa[k][l]
#print("No[",main_count,"] P",P)
def calc_ang(self):
#回転行列準備:計算簡略化のためクオータニオンの回転行列を以下のように定義
#Rot_R = [Rot_R[0] Rot_R[1] Rot_R[2]
# Rot_R[3] Rot_R[4] Rot_R[5]
# Rot_R[6] Rot_R[7] Rot_R[8]]
Rot_R[0] = xa[0]*xa[0] + xa[1]*xa[1] - xa[2]*xa[2] - xa[3]*xa[3]
Rot_R[1] = 2*(xa[1]*xa[2] + xa[0]*xa[3])
Rot_R[2] = 2*(xa[3]*xa[1] - xa[2]*xa[0])
Rot_R[3] = 2*(xa[1]*xa[2] - xa[3]*xa[0])
Rot_R[4] = xa[0]*xa[0] - xa[1]*xa[1] + xa[2]*xa[2] - xa[3]*xa[3]
Rot_R[5] = 2*(xa[2]*xa[3] + xa[1]*xa[0])
Rot_R[6] = 2*(xa[3]*xa[1] + xa[2]*xa[0])
Rot_R[7] = 2*(xa[2]*xa[3] - xa[1]*xa[0])
Rot_R[8] = xa[0]*xa[0] - xa[2]*xa[2] + xa[3]*xa[3] - xa[1]*xa[1]
ang_temp[0] = math.atan2(Rot_R[5],Rot_R[8])
ang_temp[1] = -math.atan2(Rot_R[2],math.sqrt(Rot_R[5]*Rot_R[5]+Rot_R[8]*Rot_R[8]))
ang_temp[2] = math.atan2(Rot_R[1],Rot_R[0])
初期値の設定に必要な値や、誤差のモデル化方法は一部省略しております。もしご要望等ありましたら別記事でまとめようかと考えております。
まとめ
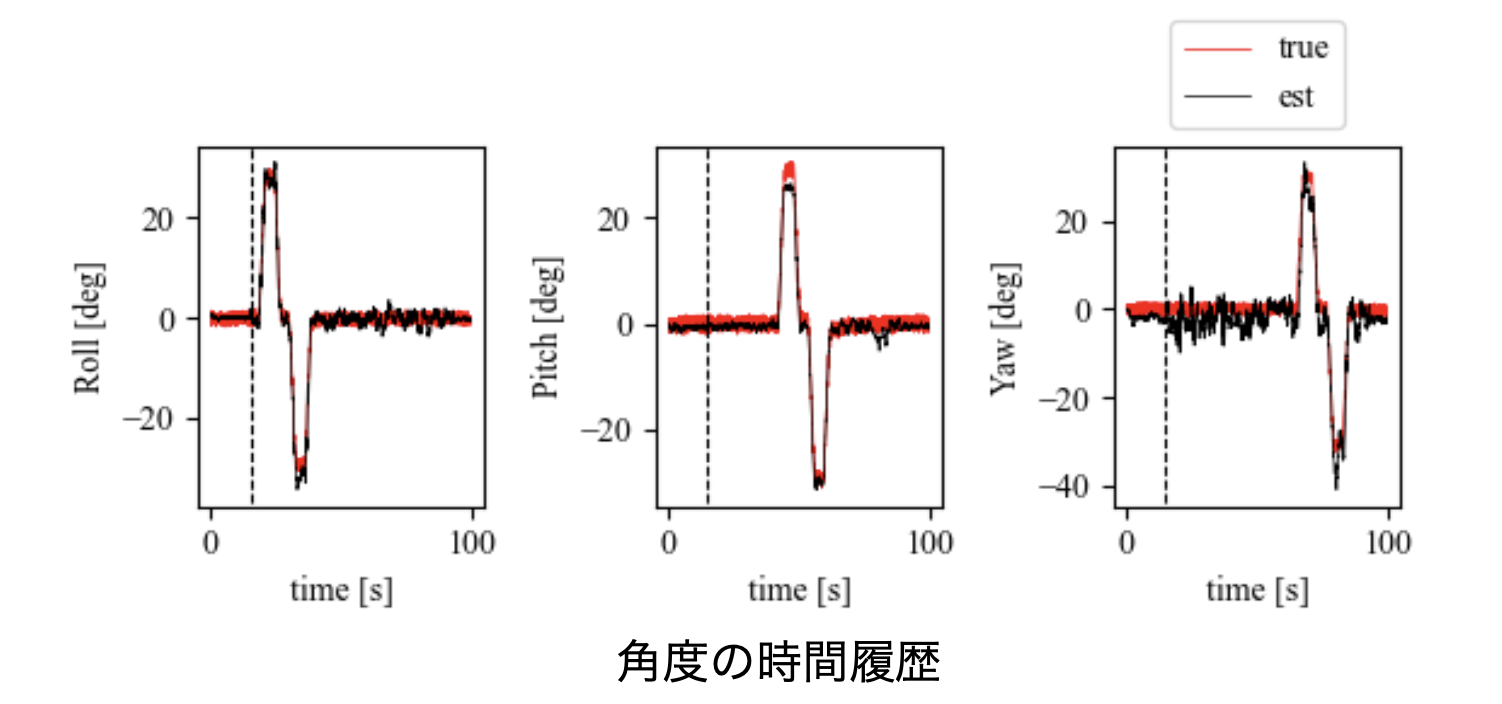
以上の理論の実装がうまくできた場合、10Hz程度以下の運動は推定可能です。
冒頭でも申し上げた通り、実際にドローンに搭載するためには300Hz以上の計算回数は必要になります。
姿勢角推定はドローンだけでなく、コントローラ(コントローラがどれくらい傾いているか、どの速度で動いたか)などを推定するためにも使用できます!
お知らせ
現在ABEJAでは一緒にAIの社会実装を進める仲間を募集しています!
世の中をアップデートする最前線の現場に、あなたも飛び込んでみませんか?
【募集職種一覧はこちら!】