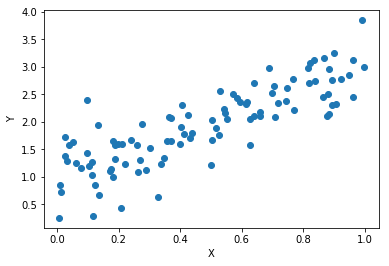
線形回帰
$N$個のデータの組 $(x_i, y_i)$ があるときにその関係 $y = a x+b$ を求めよ
推定
観測データからパラメータを計算する関数
$$\hat{a} = \phi_a(\hat{x}, \hat{y}), \hat{b} = \phi_b(\hat{x}, \hat{y})$$
を推定量と呼ぶ。
- 観測データがランダムに生成されていると、そこから計算した推定量もランダムな値を取る
- 推定量のうち、その期待値 $E[\hat{a}]$ が真のパラメータ値 $a$ に一致するものを不偏推定量と呼ぶ
最尤推定
- パラメータがある値 $a, b$ だった時にそのデータが出力される確率 $p(x,y|a,b)$ を 尤度 と呼ぶ
- 尤度を計算するにはノイズを含めた 確率モデル が必要
- ノイズは正規分布に従ってると仮定する($\sigma^2$は簡単のため既知とする):
$$ p(x,y|a,b) = \mathcal{N}_{\sigma^2}(y-(ax+b)) \propto \exp(-|y-(ax+b)|^2/2\sigma^2) $$ - 個々の観測が独立に得られていると仮定する:
$$ p(\hat{x}, \hat{y}|a, b) = \prod_i p(x_i, y_i|a, b) $$ - 尤度が最高になるように$a, b$を選ぶ(最尤推定):
$$ \phi_{a,b}(\hat{x}, \hat{y}) = \text{argmax}_{(a, b)} p(\hat{x}, \hat{y}|a, b)$$
最小二乗法
- $\log$は単調増加関数なので$p(..)$の最大値は$\log(p(..))$の最大値と同じ:
$$ \log(p(\hat{x}, \hat{y}|a, b)) = \sum_i \log(p(x_i, y_i|a, b)) = -\sum_i |y_i -(ax_i +b)|^2/2\sigma^2 $$ - これが最小二乗法のコスト関数
- $a, b$に対する2次式なので平方完成できる
- 実際$\sigma^2$は計算に出てこない
ベイズ線形回帰
- パラメータの確率分布を考える $p(a, b)$
- パラメータの事前分布を仮定する:
$$ p(a, b) \propto \exp(-(a^2 + b^2)/2\sigma_a^2)$$ - 観測データ$(x_i, y_i)$が入るたびに更新する(事後分布)
$$ p(a,b| \hat{x}) \propto p(\hat{x}|a,b) p(a,b) $$ - 事後分布に対して最尤推定を行う:
$$ \log(p(\hat{x}, \hat{y}|a,b)) = -\sum_i |y_i -(ax_i +b)|^2/2\sigma^2 - (a^2+b^2)/2\sigma_a^2$$ - 正則化項が追加され、$\sigma^2$に意味が出てくる
Evidence function
- ハイパーパラメータ$\sigma^2$, $\sigma_a^2$はどうやって決めればよかったのか?
- $\sigma^2$, $\sigma_a^2$を決めると$a$, $b$の推定量$\phi_{a,b}$が一意に決まるのでそれについて平均をとる(Eステップ)
$$
p(\hat{x}, \hat{y}|\sigma^2, \sigma_a^2) = \int da \int db p(\hat{x}, \hat{y}|a, b, \sigma) p(a, b|\sigma_a^2)
$$ - これを最大化する$\sigma^2$, $\sigma_a^2$が良いハイパーパラメータ
- でもどうやって計算する??
EMアルゴリズム
- $p(\hat{x}, \hat{y}|\sigma^2, \sigma_a^2)$ の最大化問題では$(a, b)$は積分されてしまっているので、隠れ変数とみなせる
- EMアルゴリズムは観測できる変数($X$)と隠れ変数($Z$)がある場合のパラメータ($\theta$)を最尤推定するためのアルゴリズム
$$ p(X|\theta) = \int dZ p(X, Z|\theta) $$
EMアルゴリズム(for ベイズ線形回帰)
- Eステップ:固定したハイパーパラメータ($\sigma^2, \sigma_a^2$)に対してパラメータ$a, b$の事後分布$p(a,b|\hat{x}, \hat{y})$を計算する
- Mステップ:その分布に対して平均した $E_{a,b}[\log p(\hat{x}, \hat{y}, a, b|\sigma^2, \sigma_a^2)]$を最大化する