スクリプト
- ポアソン過程でステップするトラジェクトリのステップ地点を検出するアルゴリズム
- "Assembly dynamics of microtubules at molecular resolution" Nature (2006) 709-712 を参考に作成
- 一番大きいステップをはじめに検出して、だんだん小さいステップを足していくスタイル
- このアルゴリズムのいいところはフリーパラメータが実質ゼロでCalibrationの必要がないところ
- 前に作ったpoisson_stepper.pyを使用してテスト
chi2.py
# !/usr/bin/python
import matplotlib.pyplot as plt
import numpy as np
import poisson_stepper
from scipy.optimize import curve_fit
import time
import timer
def detect_step(trajectory):
# Initialize
min_chi2 = float("inf")
min_t = 0
delta_times_length = 0.0
n = len(trajectory)
for i in range(1, n - 1):
# Array preparation
left = trajectory[0:i]
right = trajectory[i:n]
# Calculate Chi2
current_chi2 = len(left) * np.var(left) + len(right) * np.var(right)
# Update minimum values
if min_chi2 > current_chi2:
min_chi2 = current_chi2
min_t = i
delta_times_length = abs(np.average(left) - np.average(right)) * n
return min_t, delta_times_length
def plot(trajectory, border, average_trajectory):
plt.plot(trajectory)
for i in range(1, len(border)):
x = np.arange(border[i-1], border[i], 0.1)
y_value = average_trajectory[i-1]
y = [y_value for _ in range(0, len(x))]
plt.plot(x, y, color='k', linewidth=2.0)
if i == len(border) - 1:
break
y = np.arange(average_trajectory[i-1], average_trajectory[i], 0.1)
x = [border[i] for _ in range(0, len(y))]
plt.plot(x, y, color='k', linewidth=2.0)
plt.show()
def detect_step_all_ranges(trajectory, border):
max_delta_times_length = 0.0
max_step_t = 0
for iborder in range(0, len(border)-1):
start = border[iborder] + 1
end = border[iborder+1] - 1
trajectory_to_process = trajectory[start:end]
step_t, delta_times_length = detect_step(trajectory_to_process)
step_t += start
if max_delta_times_length < delta_times_length:
max_delta_times_length = delta_times_length
max_step_t = step_t
return max_step_t
def chi2(trajectory, t):
# Calculate border
border = [0, len(trajectory)]
for i in range(0, 10):
border.append(detect_step_all_ranges(trajectory, border))
border = sorted(border)
# Calculate average trajectory
average_trajectory = [np.average(trajectory[border[i]:border[i+1]])
for i in range(0, len(border) - 1)]
# Plot
plot(trajectory, border, average_trajectory)
# Calculate step size
step_size = [average_trajectory[i+1] - average_trajectory[i]
for i in range(0, len(average_trajectory)-1)]
return step_size
if __name__ == "__main__":
trajectory, t = poisson_stepper.poisson_stepper(sigma=10.0)
step_size = chi2(trajectory, t)
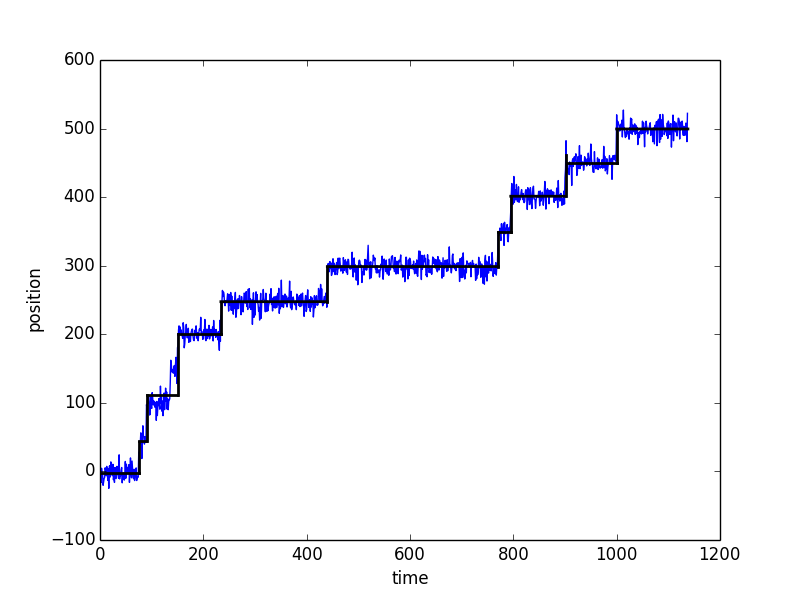
計算結果
- 青線が模擬実験データ、黒線がフィッティング
- まぁまぁ、いい精度で検出できている