はじめに
これは学生時代に勉強していたテンソルネットワークを再度まとめたものになっております。ネット上にはテンソルネットワークの解説はありますが、ソースコードが公開されているのはあまりないので、今回はテンソル繰り込み群(Tensor Renormalizations Group, 以下 TRG)を例に解説とソースコードをあげさせていただきます。
本稿が、何かに役立てば幸いです。なお、間違いなどがございましたらご指摘していただけたら幸いです。できる限り対応させていただきたいと思います。
なお、本稿及びプログラムは金沢大学の武田真滋様の資料1を参考に作成いたしました。大変わかりやすい資料ですので、一読をおすすめいたします。
また、参考資料の数式が非常に詳しく書かれているため、数式の結果だけを記述しております。なお、一部文字などを改変しております。
概要
テンソルネットワークとは、量子多体系の基底状態を求める数値計算の手法として開発されました。このテンソルネットワークはモンテカルロ法での符号問題が存在しない、巨大な体積の計算が可能という様々な利点があります。また、物理学の諸問題だけではなく機械学習の分野でも応用されるなど、個人的にホットトピックだと思っております。本稿では先に述べたとおり、二次元イジングをテンソルネットワーク表記で表し、TRG を用いて厳密解を求めてみたいと思います。
実行環境
今回の実行環境は次のようになります。
- Ubuntu 18.04LTS
- Ryzen 7 3700X
- RAM 16GB
- Python(miniconda) ver 3.8.8
- numpy ver 1.19.5
- Pytorch 1.8.0
テンソルネットワークとは
テンソルネットワークとは、量子多体系の波動関数、統計力学の分配関数などを多数のテンソルの縮約として表現する手法です。
まず、テンソルというのは、次のようなものを言います。
A_{ij}\\B_{ijk}\\C_{ijkl}
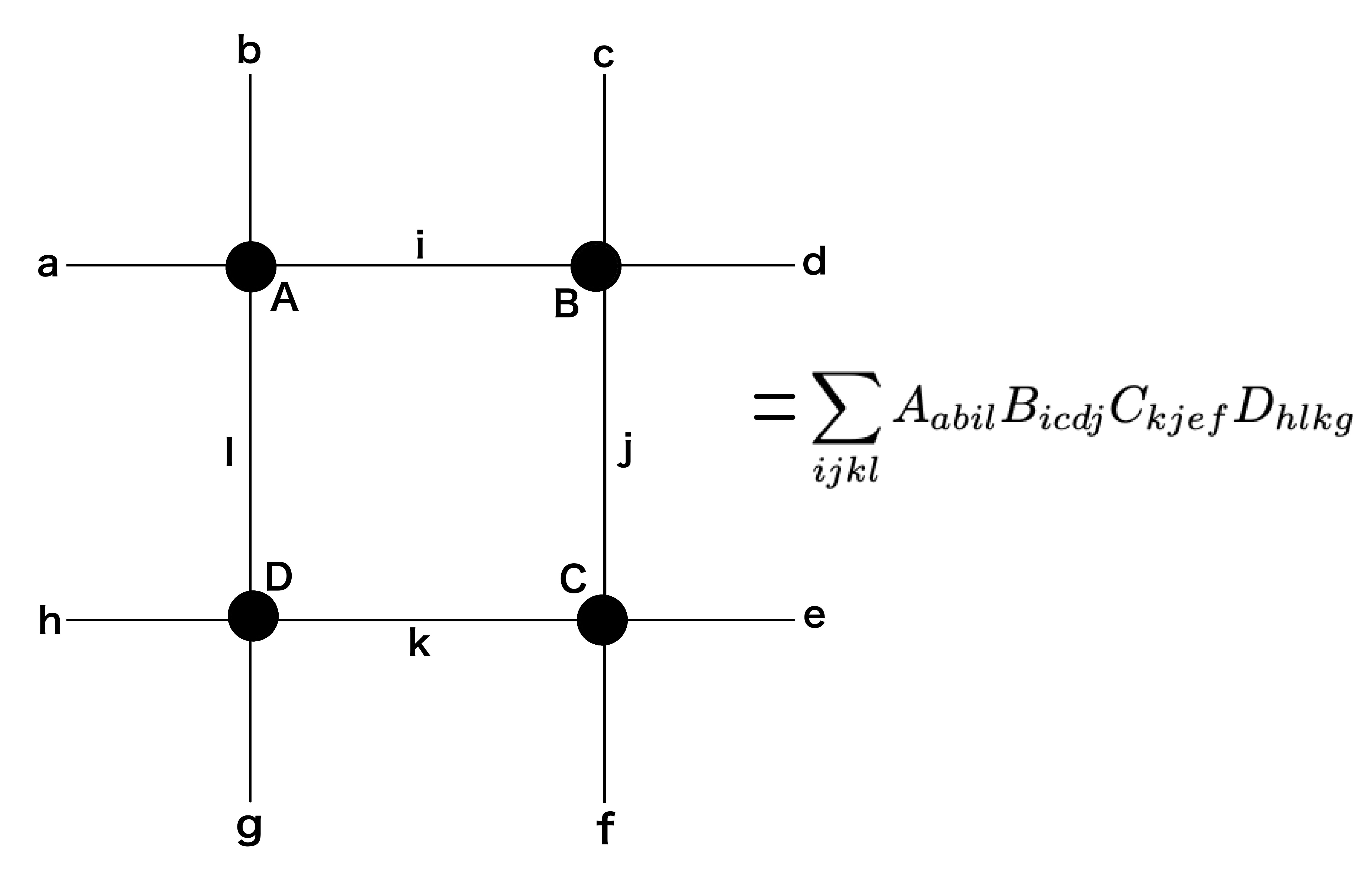
Aがランク2のテンソル、B がランク3のテンソル、C がランク4のテンソルといい、それぞれの添字は足と呼ばれます。量子力学を学んだ方ならとっつきやすいかもしれません。さて、ランク4のテンソルが4つあった場合、それらをテンソルネットワークで表すと次のようになります。
上記図の数式をみると ijkl で和を取ることになります。アインシュタインの縮約記法と似ています。
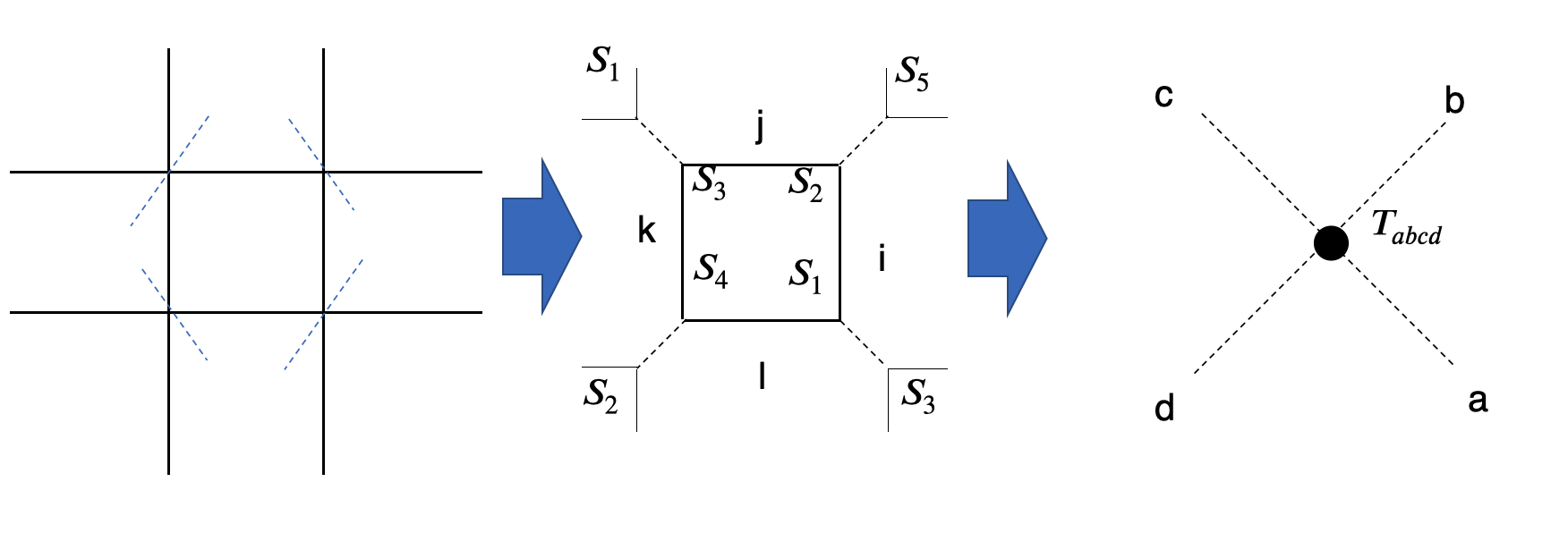
TRGでは、上記図の正方形のネットワークが複数個結合するネットワークとなります。
二次元イジングのテンソルくりこみ群
繰り込み群の流れは
- 二次元イジングの分配関数をテンソルネットワーク表示にする。
- テンソルを特異値分解し、新しい添字を用いて2つのテンソルに分ける。
- 古い添字の和を実行して新しいテンソルを作る。
- 2と3を繰り返し、途中でDをDcutにし低ランク行列による近似を行う。
- 最後にテンソルのトレースを取る。
テンソルネットワーク表示
まず、二次元イジングの分配関数Zをテンソルネットワーク表示1にします。
Z = \sum_s \exp{(\sum_{}\beta s_x s_y)} = 2^V(\cosh{\beta})^{2V}\sum_{\dots ijkl \dots} \dots T_{ijkl}T_{mnop} \dots\ \ast T_{ijkl} = (\sqrt{\tanh{\beta}})^{i_{xy}+i_{xz}+i_{xw}+i_{xv}}\delta(mod(i_{xy}+i_{xz}+i_{xw}+i_{xv},2))
このとき Tijkl を2次元の行列として表すと(4x4行列になります。添字は最初は0か1のみ数値を取るようになっております。)
\left(
\begin{array}{ccc}
T_{0000} & \dots & T_{0011}\\
\vdots & \ddots & \vdots\\
T_{1100} & \dots &T_{1111}
\end{array}
\right)
=
\left(
\begin{array}{cccc}
1&0&0&\tanh{\beta}\\
0&\tanh{\beta}&\tanh{\beta}&0\\
0&\tanh{\beta}&\tanh{\beta}&0\\
\tanh{\beta}&0&0&(\tanh{\beta})^2
\end{array}
\right)
となります。
この初期の行列を作成するソースコードは
class initial_tensor():
def Delta_func(self,x):
y= np.array([0.,1.],dtype='float64')
if x ==0:
return y[1]
else:
return y[0]
def Tensor(self,K):
K = torch.tensor(K,dtype=torch.float64,device=torch.device("cpu"))
T = torch.zeros(2,2,2,2,dtype=torch.float64)
for i in range(2):
for j in range(2):
for k in range(2):
for l in range(2):
T[i,j,k,l] += (torch.sqrt(torch.tanh(1/K))**(i+j+k+l) * self.Delta_func(np.mod(i+j+k+l,2)))
T = T.view(2,2,2,2)
return T
になります。後のテンソルの扱いを楽にするため、4次元のテンソルとして扱っています。今後添字の数=次元として扱うようにしています。
テンソルの分解
テンソルの分解は特異値分解 (SVD) を実行します。テンソルの分解方法は次の二通りあります。
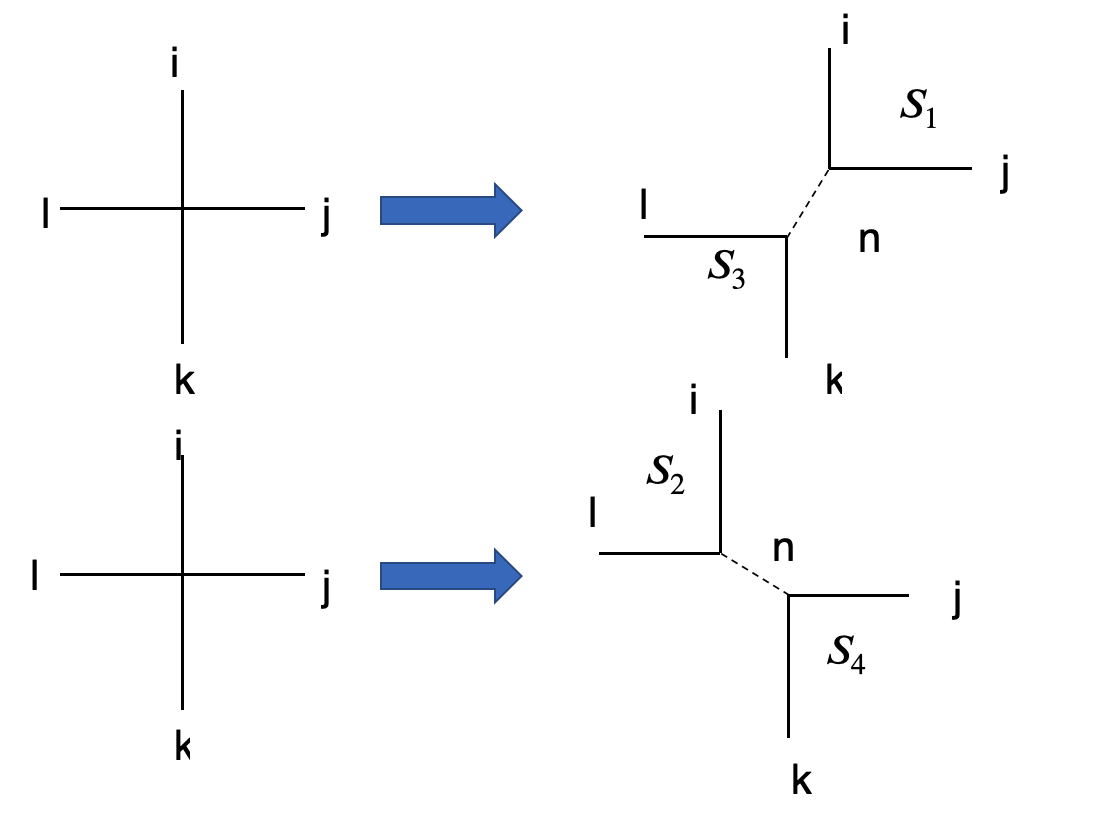
これを式で表すと
T_{ijkl} = \sum^{D^2}_{n=1}u_{ijn}\sqrt{s_n}\sqrt{s_n}v^{\dagger}_{nkl} = \sum^{D^2}_{n=1}(S_1)_{ijn}(S_3)_{kln}\\
T_{ijkl} = \sum^{D^2}_{n=1}u_{iln}\sqrt{s_n}\sqrt{s_n}v^{\dagger}_{njk} = \sum^{D^2}_{n=1}(S_2)_{iln}(S_4)_{jkn}
とそれぞれ対応しております。
このときの、記号の対応は
n = i+D(j-1)\
k,j = 1,2,\dots,D\
n = 1,2,\dots,D^2
となります。
Ma = T.view(D**2,D**2)
ua,sa,va = torch.svd(Ma)
Mb = T.permute(1,2,3,0).contiguous().view(D**2,D**2)
ub,sb,vb = torch.svd(Mb)
.viewというのはテンソルを任意の大きさに変更するものです。このときはランク4のテンソルをランク2のテンソルに変更します。このとき、要素数は一緒になります。
T.permute(1,2,3,0).contiguous()というのは、行列の入れ替えに対応します。今回はテンソルの各次元の順番を入れ替えました。たとえばij行とkl列に対応するのをjk行とli列に変更するのに一致します。行列の分解方法はしっかりと違うので注意してください。私はこれで悩みました。
新しいテンソルを作成
この式は
T_{abcd} = \sum^{ALL}{i,j,k,l}(S_1){ila}(S_2){jib}(S_3){kjc}(S_4)_{lkd}
で表せます。
ここでは
def S_n(self,x,y,D,D_cut):
u = (x[:,:D_cut]).view(D,D,D_cut)
s = torch.sqrt(y[:D_cut])
return torch.einsum('kjm,m->kjm',u,s)
低ランク近似とトレース
Dが大きくなっておくと、その分テンソルが大きくなってしまいます。そうなると、計算に時間が非常にかかってしまいます。そのため、途中で低ランク近似を行います。
T_{ijkl} = \sum^{D^2}{n=1}(S_1){ijn}(S_3){kln} \approx \sum^{Dcut}{n=1}(S_1){ijn}(S_3){kln}\
T_{ijkl} = \sum^{D^2}{n=1}(S_1){iln}(S_3){jkn} \approx \sum^{Dcut}{n=1}(S_1){ijn}(S_3){kln}
テンソルの分解と新しいテンソルの作成を繰り返し、途中で低ランク近似を行い続けると最終的に 残るテンソルは一つになります。それのテンソルのトレースが分配関数の近似になります。
プログラム全体
以上より、分配関数が求まったため、比熱を計算するとそのピークとなる温度が厳密解になります。
ソースコードを一括で表示すると
import matplotlib.pyplot as plt
import numpy as np
import torch
from torch import einsum
from torch.linalg import svd
import time
class initial_tensor():
def Delta_func(self,x):
y= np.array([0.,1.],dtype='float64')
if x ==0:
return y[1]
else:
return y[0]
def Tensor(self,beta):
beta = torch.tensor(beta,dtype=torch.float64,device=torch.device("cpu"))
T = torch.zeros(2,2,2,2,dtype=torch.float64)
for i in range(2):
for j in range(2):
for k in range(2):
for l in range(2):
T[i,j,k,l] += (torch.sqrt(torch.tanh(beta))**(i+j+k+l) * self.Delta_func(np.mod(i+j+k+l,2)))
T = T.view(2,2,2,2)
return T
class TRG():
def S_n(self,x,y,D,D_cut):
a = (x[:,:D_cut]).view(D,D,D_cut)
b = torch.sqrt(y[:D_cut])
return torch.einsum('kjm,m->kjm',a,b)
def Renorm(self,T,Dcut):
D = T.shape[0]
D_cut = min(D**2, Dcut)
Ma = T.view(D**2,D**2)
ua,sa,va = torch.svd(Ma)
Mb = T.permute(1,2,3,0).contiguous().view(D**2,D**2)
ub,sb,vb = torch.svd(Mb)
# einsum 'ila,jib,kjc,lkd->abcd' S1,S2,S3,S4
return torch.einsum('ila,jib,kjc,lkd->abcd', (self.S_n(ua,sa,D,D_cut),self.S_n(ub,sb,D,D_cut), self.S_n(va,sa,D,D_cut), self.S_n(vb,sb,D,D_cut)))
def Loop_func(self,T,loop,Dcut):
norm = 0.
for i in range(loop):
T_new = T/T.abs().max()
norm+= torch.log(T.abs().max())/(2**(i))
T = self.Renorm(T_new,Dcut)
D = T.shape[0]
logZ = torch.log(torch.trace(T.view(D*D,D*D)))
return(logZ/2**loop) +norm
Dcut = int(input("Dcut:"))
loop = int(input("Number of renormalizations:"))
s_beta = 0.4
e_beta = 0.5
step = 51
temp = []
logZ_list = []
for beta in np.linspace(s_beta,e_beta,step):
T = initial_tensor().Tensor(beta)
start = time.time()
logZ = TRG().Loop_func(T,loop,Dcut) + np.log(2) + 2*np.log(np.cosh(beta))
run_time = time.time()-start
print('beta : {:.4f},trace(logZ/V):{:.5f},run time:{:.2f}'.format(beta,logZ,run_time))
temp.append(beta)
logZ_list.append(logZ)
# temp.logZ_list
def Energy(x,y):
size = len(x)-1
E_list = []
E_Beta_list = []
for i in range(size):
d_beta = x[i+1]-x[i]
d_log = y[i+1] - y[i]
E_list.append(-1*d_log/d_beta)
E_Beta_list.append((x[i+1]+x[i])/2)
return E_Beta_list,E_list
def S_heat(x,y):
size = len(x)-1
Cv_list= []
Cv_beta_list = []
for i in range(size):
d_beta = x[i+1]-x[i]
d_E = y[i+1] - y[i]
beta = (x[i+1]+x[i])/2
Cv_list.append(-1*beta*beta*d_E/d_beta)
Cv_beta_list.append(beta)
return Cv_beta_list,Cv_list
def Sort_heat(x,y):
y_r = sorted(y)
y_r.sort(reverse = True)
a = y_r[0]
b = y.index(a)
c = x[b]
a = a.to('cpu').detach().numpy().copy()
return c,a
E_Beta_list,E_list = Energy(temp,logZ_list)
Cv_beta_list,Cv_list = S_heat(E_Beta_list,E_list)
Max_beta ,Max_Heat = Sort_heat(Cv_beta_list,Cv_list)
fig = plt.figure()
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['xtick.direction'] = 'in'
x = Max_beta*1.5
y = Max_Heat/10
fig.add_subplot(xlim=(s_beta,e_beta),ylabel="Heat",xlabel="Beta")
fig.text(x,y,'Max_heat:{:.4f}\nbeta : {:.2f}'.format(Max_Heat ,Max_beta ),size=12)
plt.plot(Cv_beta_list,Cv_list)
fig.savefig("Heat_{}_{}.png".format(Dcut,loop))
上記プログラムでの
def Loop_func(self,T,loop,Dcut):
norm = 0.
for i in range(loop):
T_new = T/T.abs().max()
norm+= torch.log(T.abs().max())/(2**(i))
T = self.Renorm(T_new,Dcut)
D = T.shape[0]
logZ = torch.log(torch.trace(T.view(D*D,D*D)))
return(logZ/2**loop) +norm
では、オーバーフローを防ぐためにくりこみをするテンソルTを規格化しています。それぞれのループではその時の体積で割ることにしています。
結果
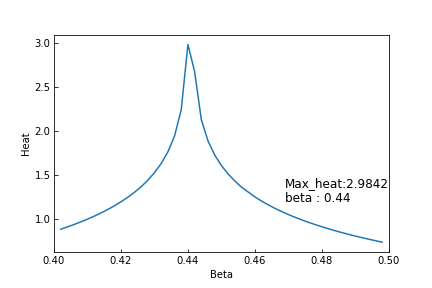
上記プログラムの実行結果がこちらになります。
Dcut=32,くりこみ回数(loop)=20のときの結果です。およその実行時間は約7分ほどとなっております。(温度のメッシュは51となっております。1度辺り7秒ほどかかっている計算になります。)
比熱は
次は β 表示ではないですが、くりこみ回数による違いは次のようになります。Dcut=32となっております。
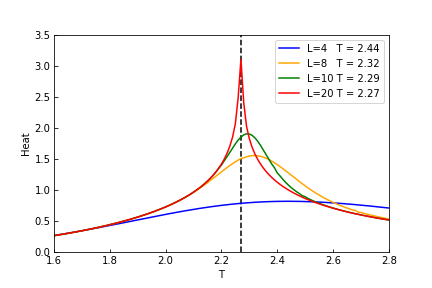
比熱のピークがT = 2.27となっており厳密解=2.269...1に近い値となっております。
上の図と下図の赤い線を比較するとスケールの違いからかBetaでの計算よりケルビンでの計算のほうがスムーズに見えます。メッシュのスケールが違うからでしょう。
まとめ
今回は、主としてプログラムや数式とプログラムの対応を中心に記述しました。
なかなか、プログラムで書き起こすのは苦労しましたが、最終的な結果は満足する出来だと思います。
テンソルネットワークは機械学習、ディープラーニングなどにも応用は利くので、今後何かしらの応用したプログラムを組んでいきたいと思います。
参考文献
-
著者:武田真滋様 タイトル:テンソルくりこみ群による素粒子物理学の諸問題へのアプローチ
- 筑波大学のシンポジウムでの資料のようです。