3Dプロットライブラリ MayaVi を Julia から使う

【注意】 この記事は、2016年12月に公開したものです。 以下のコードは Julia 0.6 向けです。

Julia advent calendar 2016 6日目の記事です。

最近 condaパッケージが提供されるようになった MayaVi というライブラリを、Julia から使ってみます。

MayaVi とは

　MayaVi は 3次元プロットのためのパッケージです。概略は、以下の通りです。

• 科学技術計算のコンサルタント会社 Enthought社 が開発している Python向け 3次元プロットパッケージ。 同社が配布する統合環境 Enthough Canopy に含まれています。また、Windows向けの科学技術計算Pythonパッケージ Python(x,y) に含まれています。
• 描画エンジンは、C++で書かれたライブラリ The Visualization Toolkit (VTK) です。 vtkは、大規模・複雑なデータの可視化に向いています。
• MayaVi は "Ma-ya-vee" と発音します。サンスクリット語で、英語の "magical" に相当するそうです。

　同じような性格を持つライブラリに ParaView があります。こちらは並列分散化を目指していて、MayaVi より有名でしょう。
　私は、MayaVi を先に使い始めており、ParaView をインストールした際には大変面倒であった経験があります。使い勝手は、だいたい似ていますし、個人プロジェクトでは MayaVi はおすすめです。

mayavi の conda パッケージをインストールする

　Juliaでの condaパッケージの扱いは、昨日の記事で解説しました。( conda パッケージを Juliaから追加しよう )
　Julia がインストールした miniconda 環境に mayavi ぱっけーじを追加するには Conda.add() を使います。

julia> using Conda

julia> Conda.add("mayavi")
Using Anaconda Cloud api site https://api.anaconda.org
Fetching package metadata .......
Solving package specifications: ..........

# All requested packages already installed.
# packages in environment at /Users/hs/.pyenv/versions/anaconda-2.4.0/envs/conda_jl:
... 以下略。

　自分で構築した anaconda環境に mayaviを追加するなら、シェル (コマンドライン、ターミナル)から conda コマンドをたたけばよいでしょう。

$ conda install mayavi -n conda_jl
Using Anaconda Cloud api site https://api.anaconda.org
Fetching package metadata .............
Solving package specifications: ..........

Package plan for installation in environment /Users/hs/.pyenv/versions/anaconda-2.4.0/envs/conda_jl:
... 以下略。

MayaVi functions gallery

　最初に MayaVi functions gallery の例題を試してみます。

julia> using PyCall

julia> @pyimport mayavi.mlab as mlab

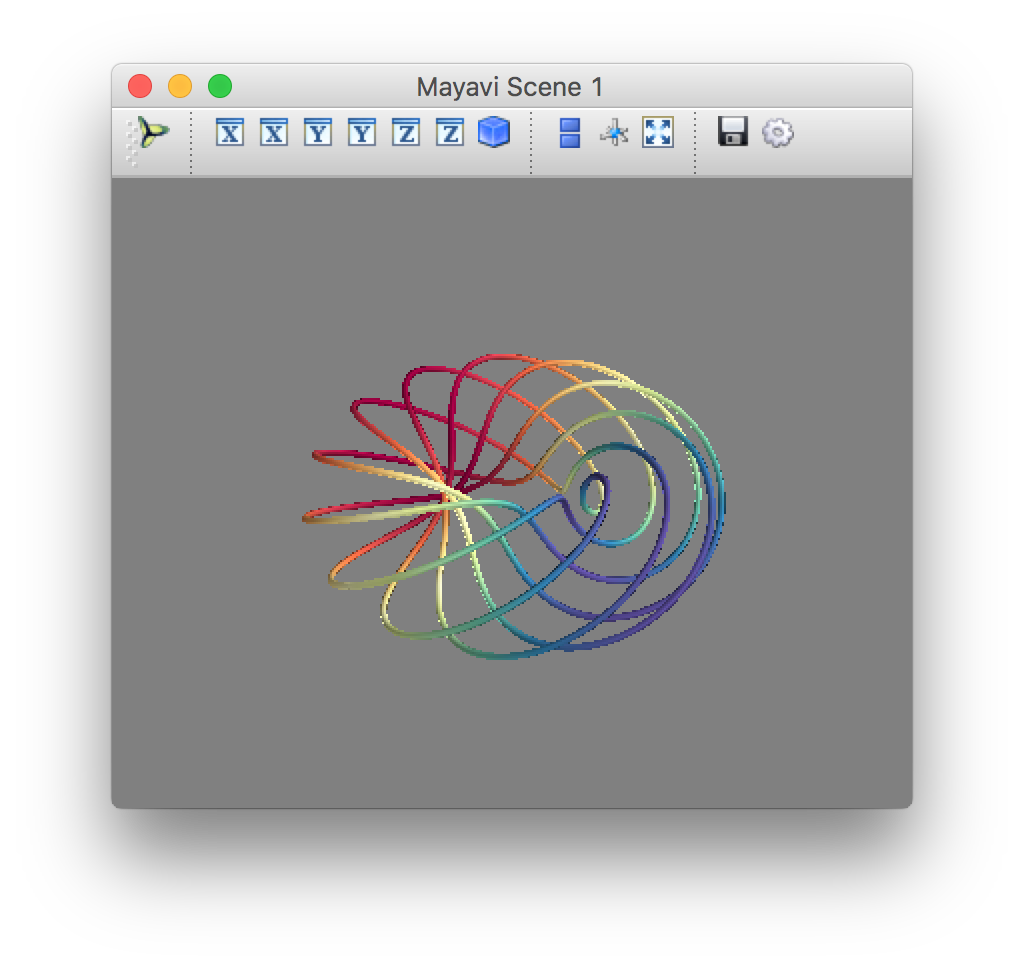
julia> mlab.test_plot3d()
PyObject <mayavi.modules.glyph.Glyph object at 0x337fc95f0>

julia> mlab.show()

上のソースファイル: plot3d() https://gist.github.com/d4578e1f4d22bbfa0f418f0caff239c7

実行結果 (スクリーンショット)

　mayavi.mlab は、Python の numpy.array を、シンプルにプロットするためのツールです。 matplotlib を知っている方には、matplotlib.pyplot に相当するといえば察していただけますか。

　mlab.show() を起動すると、実際の描画が行われます。 3次元プロットの上部に、いくつかのアイコンが並んだメニューバーがあり、図形を回転・拡大縮小することができます。この辺の機能は traits と呼ばれています (うまい訳語が見つかりません)。

　さて、Mayavi Functions gallery にある、他 8つの例題も、うまく表示できました。ソースファイルを gistに置いておきます。

• 点(球) points3d(): https://gist.github.com/a3b0b95b58a42b7b010aea779536e6f3
• 画像 imshow(): https://gist.github.com/326f9b72a56f6187f0d62b7e9e3ca4ed
• 等高面 surf(): https://gist.github.com/53d022bfcb9b268ea829f23f9e2aae4e
• 等高線 contour_surf(): https://gist.github.com/bc51e4baf2f09df352e8019e37f34bdf
• 曲面 mesh(): https://gist.github.com/8fc119d17a4bd44cefdbb7439a3a028f
• 棒グラフ barchart(): https://gist.github.com/89d6a5f3a6a321fd099d1b04e9cc7ea7
• 三角メッシュ triangular_mesh(): https://gist.github.com/3c44621b47282921458803c2c15c1aaf
• 等値面 contour3d(): https://gist.github.com/002372eecca7cc831764ea731acaf155

test_mesh() の実行結果 (スクリーンショット)

surface_from_irregular_data

　以下 4つのプログラム例を通して、Python による Mayaviプログラムを Julia に移植する際のポイントと 関連する tips を紹介します。
　surface_from_irregular_data.py というプログラムです。

• Pythonソース: http://docs.enthought.com/mayavi/mayavi/auto/example_surface_from_irregular_data.html
• 下の Julia ソース: https://gist.github.com/2cbe32c7b10a2b1c90657e06e9ba4237

function f(x, y)
  exp(-(x .^ 2 + y .^ 2))
end

srand(12345)
xs = 4.0 * (rand(500) - 0.5)
ys = 4.0 * (rand(500) - 0.5)
zs = f(xs, ys)

using PyCall
@pyimport mayavi.mlab as mlab
mlab.figure(1, fgcolor=(0, 0, 0), bgcolor=(1, 1, 1))

# Visualize the points
pts = mlab.points3d(xs, ys, zs, zs, scale_mode="none", scale_factor=0.2)

# Create and visualize the mesh
mesh = mlab.pipeline[:delaunay2d](pts)
surf = mlab.pipeline[:surface](mesh)

mlab.view(47, 57, 8.2, (0.1, 0.15, 0.14))
mlab.show()

実行結果 (スクリーンショット)

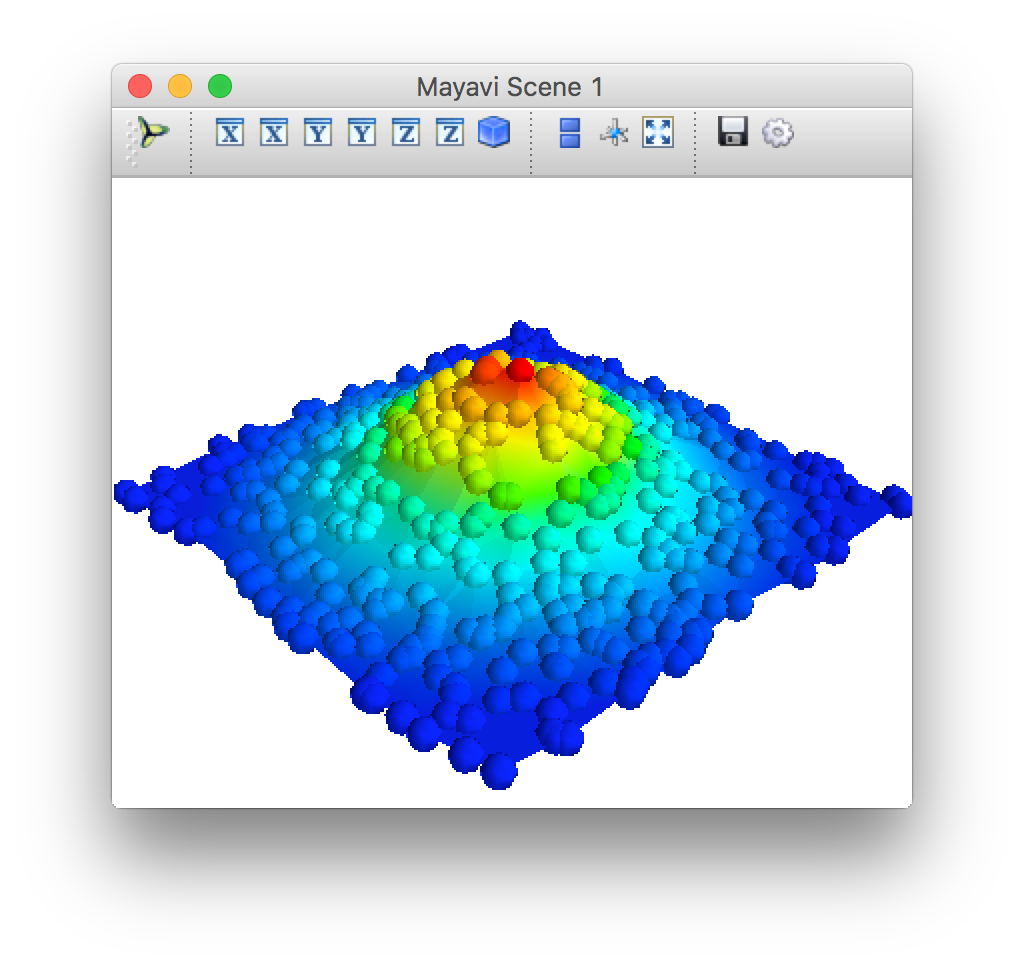
　不規則な 2次元点 (x,y) を 関数 z=f(x,y) を用いて、3次元点 (x,y,z) に拡張します。それらを点(球)として描画します(points3d)。また、3次元点を補間し(delaunay2d)、その表面を描画します (surf)。データに対して、いくつかの処理を加えていく過程はパイプライン (pipeline) と呼ばれます。
　Juliaソースは、Pythonソースとほぼ同じです。以下の点に注意しました。

• Python の mlab.pipeline.delaunay2d などは、そのまま呼べず mlab.pipeline[:delaunay2d] などとします。
• function 内で、要素毎のべき乗を .^ に修正しました。

triangular_mesh

　次に　test_triangular_mesh の中身のプログラムを、Julia に移植してみます。

• Pythonソース: http://docs.enthought.com/mayavi/mayavi/auto/mlab_helper_functions.html?highlight=triangular%20mesh#triangular-mesh
• 下の Julia ソース: https://gist.github.com/bc98e07f807ebc03f75837cb76117b79

# An example of a cone, ie a non-regular mesh defined by its triangles.
n = 8
t = linspace(-pi, pi, n)
xy = exp(im * t)
x = real(xy)
y = imag(xy)
z = zeros(n)

triangles = [ (0, i, i + 1) for i in 1:n-1 ]
unshift!(x,0.0)
unshift!(y,0.0)
unshift!(z,1.0)
t=collect(t)
unshift!(t,0.0)

using PyCall
@pyimport mayavi.mlab as mlab
mlab.triangular_mesh(x, y, z, triangles, scalars=PyObject(t))
mlab.show()

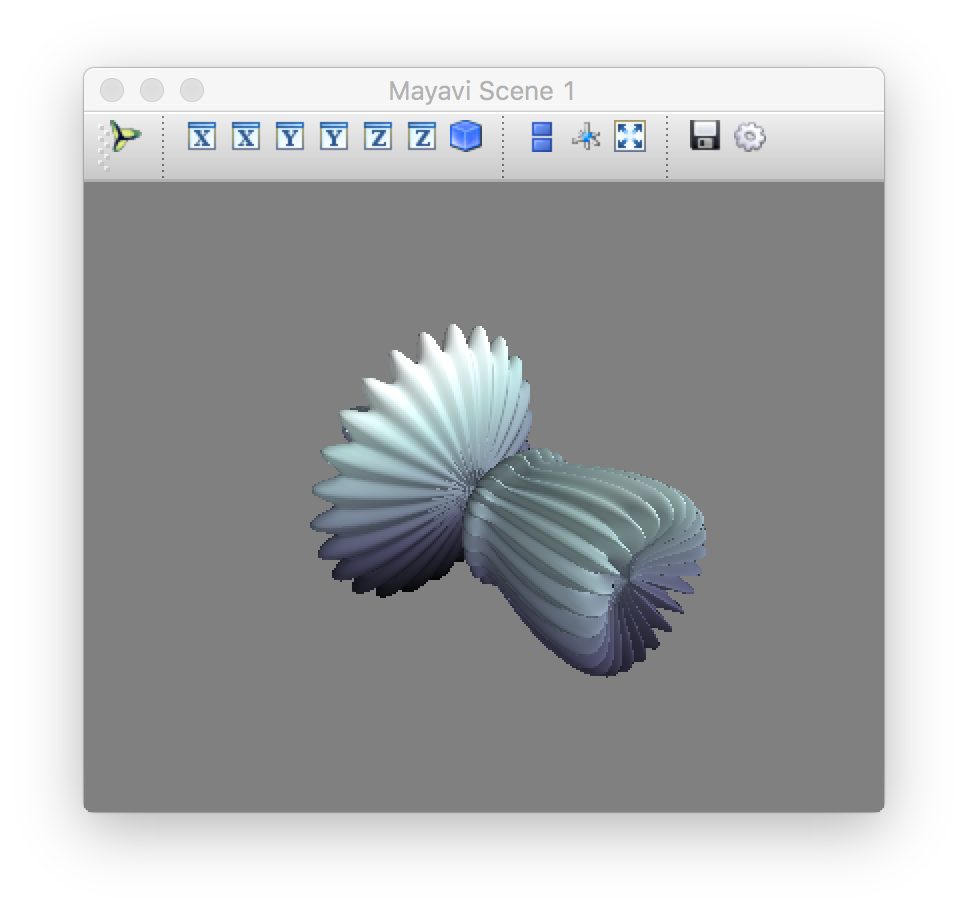
実行結果 (スクリーンショット) ※ 図形を縮小・回転しています:

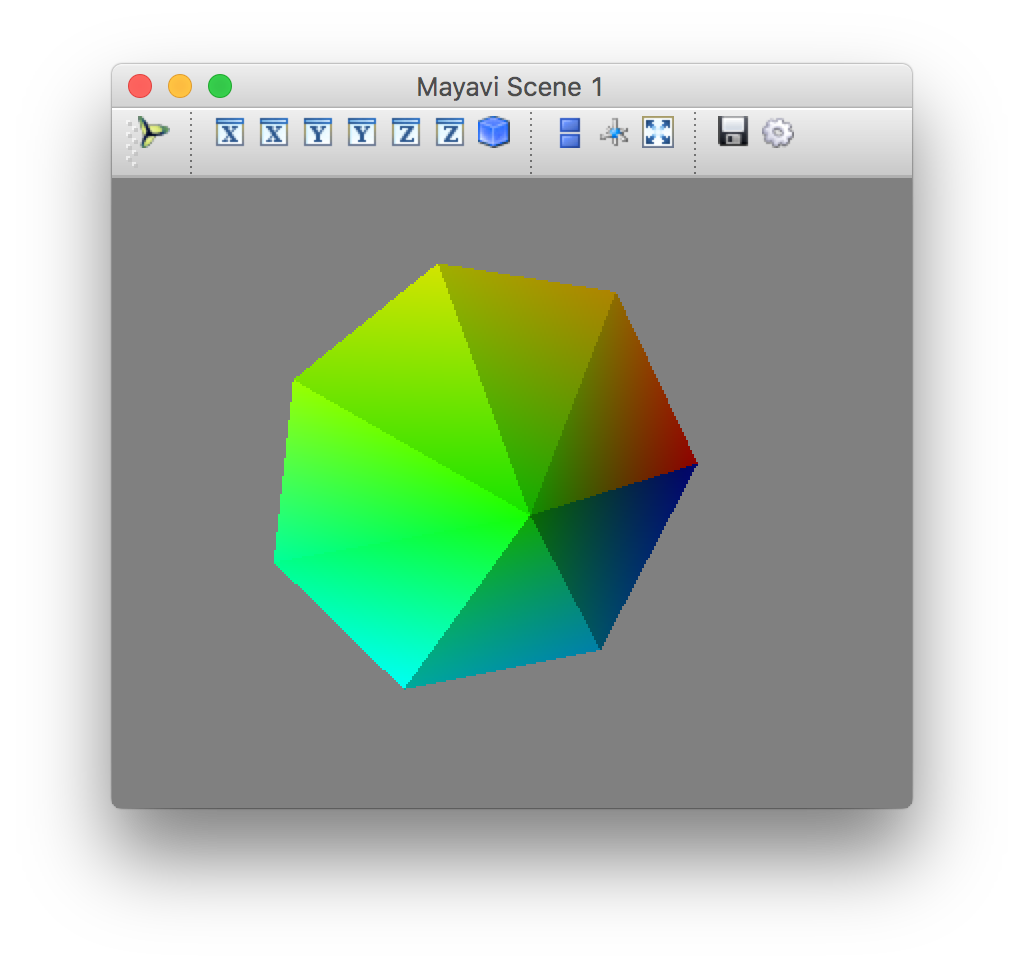
　mlab.triangular_meshは、(複数の)三角形を描画する命令です。引数として、頂点となる点の座標と、三角形の頂点の番号を与えます。 @pyimport でインポートした関数では、配列の引数を numpy.array として Python に渡します。通常のリストとして渡したいなら PyObject() でくるみます。
　注意すべきは、配列の添字が Julia では 1 から始まるのに対して、Pythonでは 0 から始まることです。 triangles で示される頂点の点番号と、Juliaでの配列添字が 1つずれることになります。

　そのほか Julia の tips をいくつか。

• linspace(start, end, n) は、要素 n 個の等差数列を作ります。数値を得るには。collect を使います。
• im は虚数単位です。
• zeros(n) は、n個の要素からなる Float64 の配列を作ります。値は 0.0 です。
• unshift!(v,e) は、配列 v の先頭に、要素 e を追加します。末尾に追加するのは push!(v,e) または append!(v,e) です。どの命令も、配列 v は破壊されます。 (命令末尾の! ですね)

spherical_harmonics

　今度は example_spherical_harmonics.py を、Juliaに移植してみます。

• Pythonソース: http://docs.enthought.com/mayavi/mayavi/auto/example_spherical_harmonics.html
• 下の Julia ソース: https://gist.github.com/60d97f20a19d820e299c253612728907

# phi, theta = np.mgrid[0:pi:101j, 0:2 * pi:101j]
phi   = [ u1 for u1 in linspace(0,pi,101), v1 in linspace(0,2*pi,101) ]
theta = [ v1 for u1 in linspace(0,pi,101), v1 in linspace(0,2*pi,101) ]

r = 0.3
x = r * sin(phi) .* cos(theta)
y = r * sin(phi) .* sin(theta)
z = r * cos(phi)

using PyCall
@pyimport mayavi.mlab as mlab
@pyimport scipy.special as spe

mlab.figure(1, bgcolor=(1, 1, 1), fgcolor=(0,0,0), size=(400, 300))
mlab.clf()
# Represent spherical harmonics on the surface of the sphere
for n in 1:6-1, m in 0:n-1
  s = real( spe.sph_harm(m, n, theta, phi) )
  mlab.mesh(x - m, y - n, z, scalars=s, colormap="jet")
  s[s .< 0] *= 0.97
  s /= maximum(s)
  mlab.mesh(s .* x - m, s .* y - n, s .* z + 1.3, scalars=s, colormap="Spectral" )
end

mlab.view(90, 70, 6.2, (-1.3, -2.9, 0.25))
mlab.show()

実行結果 (スクリーンショット)

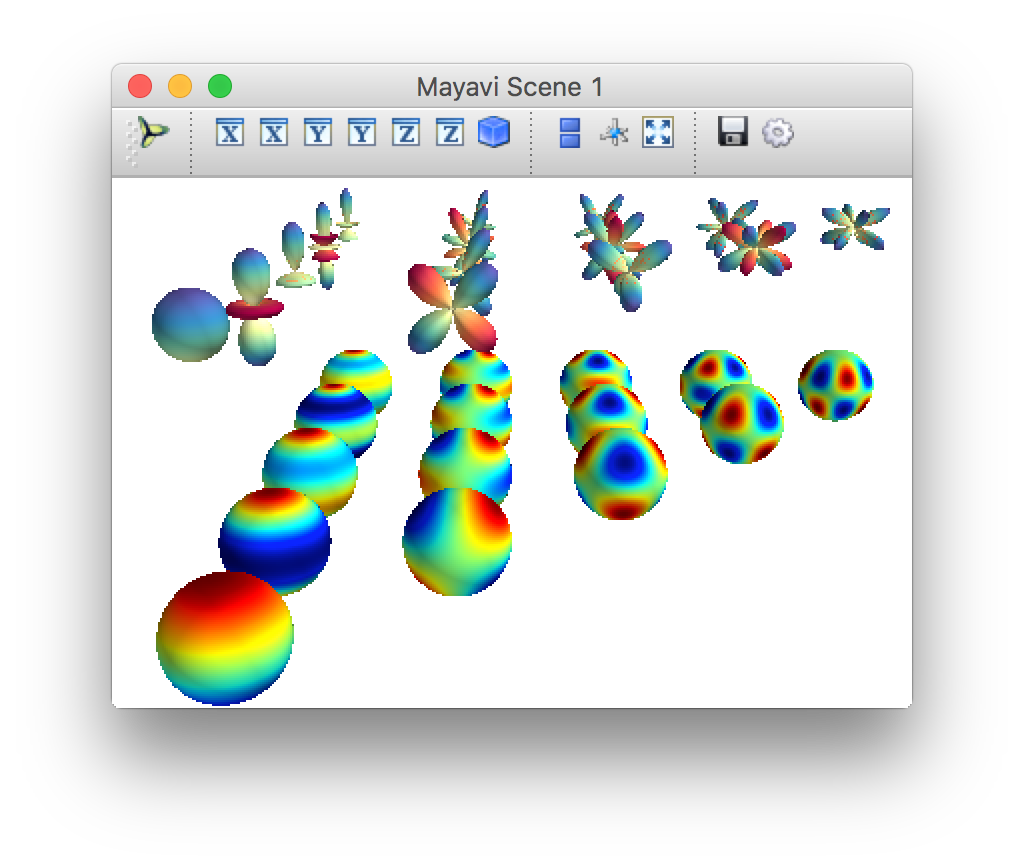
　球面調和関数の計算には Python の scipy.special.sph_harm を呼び出して計算しています。その後、曲面を描きます (mesh)。
　うまく描画できていますね。物理化学で出てくる原子軌道の方位量子数 s, p, d ... です。
　tips をいくつか。

• numpy.mgrid は、２次元座標以上の直積を作る関数ですが、Julia にはありません。しかし、その意味を考えれば、comprehension で簡単に実装できます。
• Julia の for 文は、多重ループを書けます。右に書かれたものが内側のループです。
• Python の range(n)は Julia の 0:n-1 に相当します。Python の range(m,n)は Julia の m:n-1 に相当します。

simple structured grid

　最後の例は、少し注意を要します。example_simple_structured_grid.py を、Juliaに移植してみます。

• Pythonソース: http://docs.enthought.com/mayavi/mayavi/auto/example_simple_structured_grid.html#example-simple-structured-grid
• Julia ソース: https://gist.github.com/d0c2c1c9a6fdb04c258f1961d559ee3b

# x, y, z = mgrid[1:6:11j, 0:4:13j, 0:3:6j]
x = [ x1 for x1 in linspace(1.0,6.0,11), y1 in linspace(0.0,4.0,13), z1 in linspace(0.0,3.0,6) ]
y = [ y1 for x1 in linspace(1.0,6.0,11), y1 in linspace(0.0,4.0,13), z1 in linspace(0.0,3.0,6) ]
z = [ z1 for x1 in linspace(1.0,6.0,11), y1 in linspace(0.0,4.0,13), z1 in linspace(0.0,3.0,6) ]
base=x[:,:,1] + y[:,:,1]
for i in 1:size(z)[3]
  z[:,:, i] = base[:,:] * 0.25 * (i-1)
end

pts=zeros(Float64, tuple(size(z)...,3))
pts[:,:,:,1] = x
pts[:,:,:,2] = y
pts[:,:,:,3] = z
scalars1 = x .* x + y .* y + z .* z

vectors1=zeros(Float64, tuple(size(z)...,3))
vectors1[:,:,:,1] = (4.0 - y * 2.0)
vectors1[:,:,:,2] = (x * 3.0 - 12.0)
vectors1[:,:,:,3] = sin(z * pi)

# pts = pts.transpose(2, 1, 0, 3).copy()
# pts= permutedims(pts, [3,2,1,4] )
# pts= reshape(pts, ( prod(size(pts)[1:3]), 3))

# vectors1= permutedims(vectors1, [3,2,1,4] )
# vectors1= reshape(vectors1, ( prod(size(vectors1)[1:3]), 3))

using PyCall
@pyimport tvtk.api as tvtk_api

# Create the dataset.vec
sg=tvtk_api.tvtk[:StructuredGrid](dimensions=size(x), points=pts)
sg[:point_data][:scalars] = vec(scalars1)
sg[:point_data][:scalars][:name] = "temperature"
sg[:point_data][:vectors] = vectors1
sg[:point_data][:vectors][:name] = "velocity"

@pyimport mayavi.mlab as mlab

d = mlab.pipeline[:add_dataset](sg)
gx = mlab.pipeline[:grid_plane](d)
gy = mlab.pipeline[:grid_plane](d)
gy[:grid_plane][:axis] = "y"
gz = mlab.pipeline[:grid_plane](d)
gz[:grid_plane][:axis] = "z"
iso = mlab.pipeline[:iso_surface](d)
iso[:contour][:maximum_contour] = 75.0
vec1 = mlab.pipeline[:vectors](d)
vec1[:glyph][:mask_input_points] = true
vec1[:glyph][:glyph][:scale_factor] = 1.5

mlab.show()

• 実行結果 (スクリーンショット)

• Pythonの実行結果 (スクリーンショット)

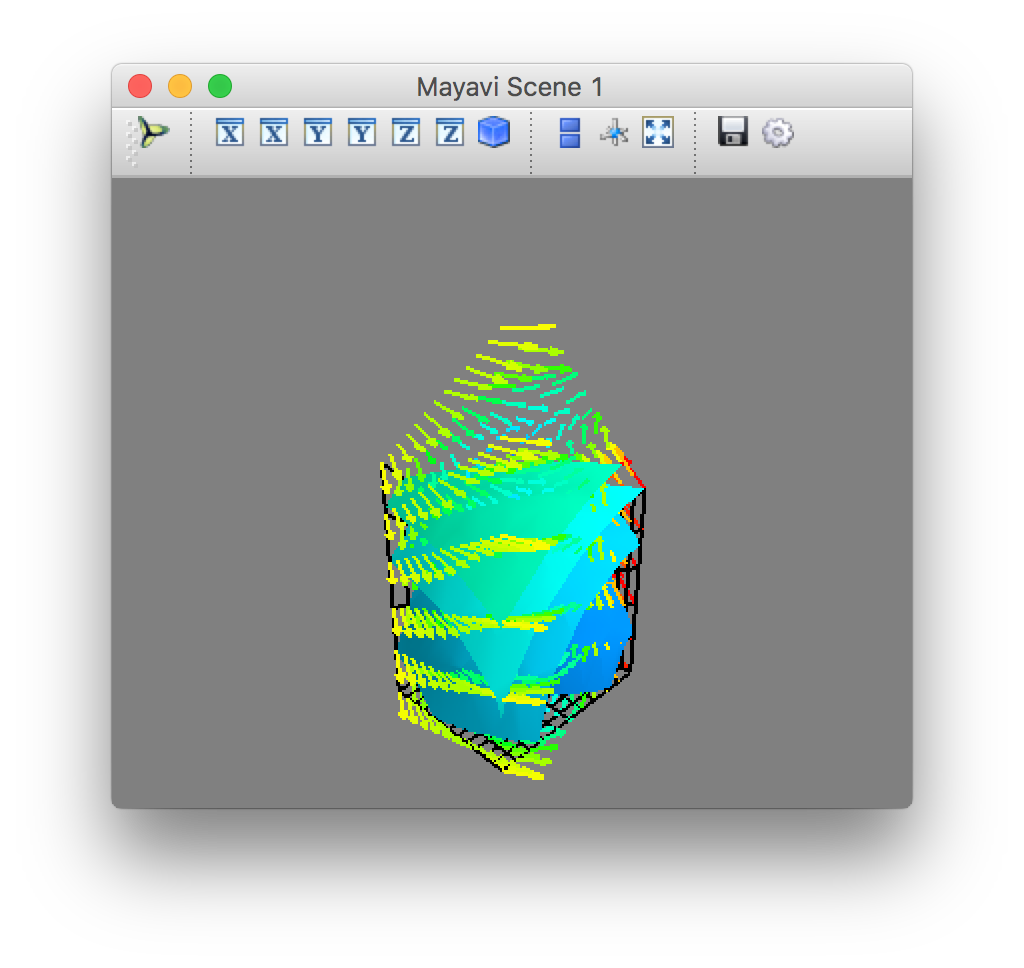
　３次元格子を作ります (StructuredGrid)。その各点で、スカラー値(scalar1)とベクトル値(vector1)を割りあてます (point_data)。これをパイプラインに流し込んで、等値面(iso_surface)とベクトル(vectors)を描画します。また、x=0, y=0, z=0 の面も描画します (grid_plane）。
　vtk に座標データを与えるときは、最初にx, 次に y、最後に z が動くように配列を与えます (column major)。python-numpy は row-major ですから、元の python ソースでは格納順を入れ替えています。これに対して、Julia は、column major ですから、そのままで大丈夫です。 (参考 Row-major orderとColumn-major order )
　ちなみに、Python の numpy.transpose 命令を、多次元配列の軸を入れ替えるのに使えます。 Juliaの transpose は 行列(2次元配列)の行と列を入れ替えるだけで、多次元配列には使えません。Julia で多次元配列の軸を入れ替えるには permutedims を使います。以下の二つが等価となります (Juliaでは、軸も 1 から数えます)。

a = a.transpose(2, 1, 0, 3).copy()

a = permutedims(a, [3,2,1,4] )
# 配列を書き換える場合
permutedims!(a, [3,2,1,4] )

　tips をいくつか。
　tuple の入れ子は展開しません。展開するには ... を付けます。splat construct といいます。

julia> ((1,2),(3,4))
((1,2),(3,4))

julia> ((1,2)...,(3,4))
(1,2,(3,4))

julia> ((1,2),(3,4)...)
((1,2),3,4)

julia> ((1,2)...,(3,4)...)
(1,2,3,4)

　多次元配列 a に対して、Python-numpyの a.shape は Julia の size(a)です。

終わりに

　以上、駆け足で、Mayavi を Julia で使う例を紹介しました。 多くの場合 Pythonソースを見ながら、ほぼ機械的に書き換えればよいことを示しました。
　さて、Mayavi を Jupyter の中で表示することもできます。これは、別の記事で紹介する予定です。-> 書きました。[Python, Julia] Jupyter で 3D 表示 - Mayavi ライブラリ