Julia Advent Calendar 2016 です。12月2日の埋め草として 12月23日に投稿しました。一人で3つも書くのは反則かしらん。
Julia では、配列の添字を 1 から数えますが (1-based array index)、Julia 0.5 では、1 以外から添字を数える機能が試験的に実装されました。該当のドキュメント Arrays with custom indices には、この機能の利用上の注意しか記載されていません。何らかのパッケージを通じて使うようです。
ここでは、OffsetArray パッケージを紹介します。Qiita記事 ラプラス方程式 内の Fortran 2008 プログラムを Julia に移植してみました。
下の Jupyter notebook: https://gist.github.com/anonymous/7437f799d132fb15e4cf0e086d5c16a9
using PyPlot
using OffsetArrays
n = 100
# real :: mesh(0:n + 1, 0:n + 1)
# mesh(0:n + 1, 0:n + 1) # Good
mesh0 = Array( Float64, n+2, n+2)
mesh = OffsetArray(mesh0, 0:n+1, 0:n+1)
mask = falses( (n,n) )
## define shape : eccentric pipe
# forall (i = 1:n, j = 1:n, (i - 51)**2 + (j - 51)**2 < 50**2) mask(i, j) = .true.
for i = 1:n, j = 1:n
if (i - 51)^2 + (j - 51)^2 < 50^2
mask[i, j] = true
end
end
# forall (i = 1:n, j = 1:n, (i - 51)**2 + (j - 71)**2 < 10**2) mask(i, j) = .false.
for i = 1:n, j = 1:n
if (i - 51)^2 + (j - 71)^2 < 10^2
mask[i, j] = false
end
end
# mesh=100.0
fill!(mesh, 100.0)
# forall (i = 1:n, j = 1:n, (i - 51)**2 + (j - 51)**2 < 50**2) mesh(i, j) = 20.0
for i = 1:n, j = 1:n
if (i - 51)^2 + (j - 51)^2 < 50^2
mesh[i, j]= 20.0
end
end
# forall (i = 1:n, j = 1:n, (i - 51)**2 + (j - 71)**2 < 10**2) mesh(i, j) = 0.0
for i = 1:n, j = 1:n
if (i - 51)^2 + (j - 71)^2 < 10^2
mesh[i, j]= 0.0
end
end
# do iter = 0, 10000
# if (mod(iter, 100) == 0) then ! character animation
# call execute_command_line('cls')
# print '(2g/, (52i1))', ' iteration =', iter, int(mesh(::2,::4) / 10.0)
# end if
# forall (i = 1:n, j = 1:n, mask(i, j)) mesh(i, j) = (mesh(i - 1, j) + mesh(i + 1, j) + mesh(i, j - 1) + mesh(i, j + 1)) / 4
# end do
for iter=0:1000
if iter % 500 == 0
# imshow(mesh[:,:]) # NG
# imshow(mesh[0:n+1,0:n+1]) # Good
imshow( parent(mesh)) # Good
end
for i = 1:n, j = 1:n
if mask[i, j]
mesh[i, j] = (mesh[i - 1, j] + mesh[i + 1, j] + mesh[i, j - 1] + mesh[i, j + 1]) / 4
end
end
end
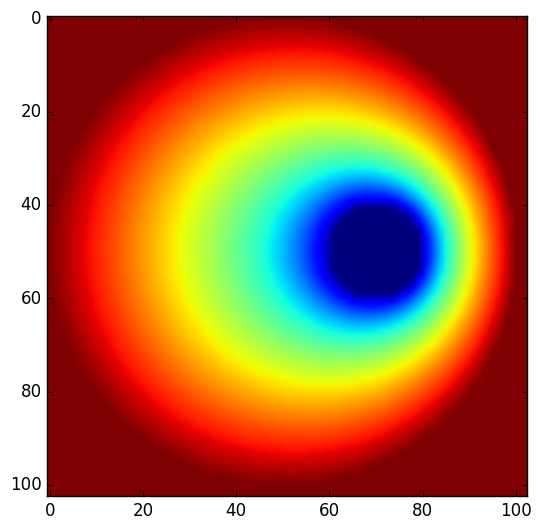
計算結果は Pyplot.imshow で表示してみました。
2次元配列 mesh が 0-based index です。Fortran 文の一部を、コメントに残しておきました。ほとんど Fortran と変わらないですね。Fortran の forall 文の 1行はよくばりすぎで、上のソースぐらいの粒度が、私は好きです。
以下 OffsetArray の使い方を一部紹介します。
■ OffsetArrays パッケージは Pkg.add("OffsetArrays") でインストールできます。使うには using OffsetArrays です。
■ OffsetArrayを確保する方法は二つあります。
n=100
# 1
a = OffsetArray(Float64, 0:n, 0:n)
# 2
a0 = Array(Float64, n+1, n+1)
a = OffsetArray(a0, 0:n, 0:n)
2は、Julia標準の 1-based index配列を、0-based添字として別名を付ける例です。 型は、このように表示されます。
a0
101×101 Array{Float64,2}:
a
OffsetArrays.OffsetArray{Float64,2,Array{Float64,2}} with indices 0:100×0:100:
■ OffsetArray は、添字を指定して読み書きする分には、通常の配列と同じように書くことができます。
■ 配列全要素を読むには、全ての範囲を添字で指定します。上の 2 の方法で確保した OffsetArray では parent(a) でもよいです。
a[0:n,0:n]
parent(a)
同じ値を OffsetArray の全要素に代入するには fill! を使います。
fill!( a, 100.0 )
a[:,:]=100.0 # NG
■ 標準の Julia の配列操作関数の多くは、OffsetArray には対応していないので使えません。
Arrays with custom indices には、以下の注意書きがあります。
-
sizeを使わない。代わりにindicesを使う -
1:length(A)をlinearindices(A)に置換する -
length(A)をlength(linearindices(A))に置換する -
Array{Int}(size(B))をsimilar(Array{Int}, indices(B))に置換する -
@boundscheckを使わない
■ その他の表現は OffsetArray の test を見るとよいです。
https://github.com/alsam/OffsetArrays.jl/blob/master/test/runtests.jl
以上駆け足で OffsetArray の使い方を実例で見ました。0-based index 向けのパッケージは、他にもあるようです。 Julia 本体の機能として提供されるとうれしいです。
[追記 2016/12/23 22:00]
OffsetArray行列の一部を取り出せますね。
julia> using OffsetArrays
julia> m0=reshape( vec(1:16), (4,4))'
4×4 Array{Int64,2}:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
julia> m=OffsetArray(m0,0:3,0:3)
OffsetArrays.OffsetArray{Int64,2,Array{Int64,2}} with indices 0:3×0:3:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
julia> m[1:2,1:2]
2×2 Array{Int64,2}:
6 7
10 11