贈るってつけるとクリスマスっぽくなるかなと思って...

どんな人に読んでもらいたいか

最近データ処理や可視化を始めた人
周りのCやfortran勢に負けずpythonで研究してる人
周りのgnuplot勢に負けずmatplotlibで可視化してる人

私は誰?

今年新卒で入社しましたテナジマと申します.
今は業務でデータ分析や機械学習を行っています.
あと野球が好きで趣味で野球の分析とかもやってます(虎党).

なぜこれを書こうと思ったか

大学生の頃は計算物理をしていました.
大学の頃も,会社に入った今もpythonを使っているのですが,大学生のときは周りがfortranやCで書いている中でのpythonだったので,技術的な進歩ってのはあまりありませんでした.
動いて正しく計算できればいい!って感じです(そうして秘伝のタレが生まれていく...).
会社に入ってからは先輩からコーディングで気をつけることや生産性が上がるためのtipsなどを教えてもらい,「うわ,これ大学生のときに知っていれば...」と思うことが多かったのでこの場を借りて伝えてあげようかなと思った次第です.
当時の僕みたいな人が一人でも救われたらこれ幸いです.

書くこと

とりあえず使おうjupyter notebook
とりあえず使おうpandas
知っておくと便利matplotlibの話~等高線の描き方を添えて~

以上の3本立てでお送りしようかなと思います.
まず言いたいこと言って,最後にデモも用意しております.

とりあえず使おうjupyter notebook

当時の僕は「えー,ブラウザ上で書くの嫌じゃ～ん」って思って食わず嫌いしてました.
そんな当時の自分にしっぺを喰らわしてやりたい気持ちでいっぱいです.
jupyterは実行環境としてやはりとても優れているので,実行はjupyterでやるってのがいい感じだなと思います.
動作確認のためのスクラッチとかとしても使えます.
可視化との相性もいいのでガシガシ使いましょう.
いちいちplt.show()とかやらなくていいですよ.

注意点

ただ一つだけ注意しておきたいのが,gitとの相性は良くないと感じています.jupyterはあくまで実行環境.scriptは別でちゃんと管理しましょう.

とりあえず使おうpandas

これも当時知っておきたかった...
jupyterと組み合わせるとデータを見ながらいじれるのですごく便利です.
しかもデータのI/Oもすごく楽!
自分しか中身の仕様がわからない謎のdatファイルを作り続け,それを読み込むための謎のscriptを作ってた自分よ,安らかに眠れ...

知っておくと便利matplotlibの話

可視化する際に使いますよね.matplotlib.
「いや,私はseaborn派だから」というそこの奥様もぜひmatplotlibの基本的なお話は抑えといたほうがいいですわよ.
というかこの記事が全て
この記事に学生の頃出会っていたかった.
この記事を読むとmatplotlibに関するググり力が格段に上がります.段違いです!
「こういうの表示したいけど,そういうメソッドはあいつが持ってそうだな」って当たりをつけてググり始められます.
ドキュメントも読みやすくなります.seabornのメソッドが持ってるaxとも仲良くなれます.
とりあえずplt.plot(hoge)みたいなことは書かなくなりました.

~等高線の描き方を添えて~

言いたいことは言ったのでデモ的なものも添えます.
今回題材とするのは等高線.
matplotlibで描こうとするとちょっと癖があるデータ処理があるんですよねー.
これを描いていきましょう.
実際に学生の頃使ってた論文のポテンシャル地形を描いていきます(その論文)

これの上の図の等高線を書きたい!(黒線は論文の内容のやつなので無視してください.詳しく知りたかったら研究内容だったので聞いてください.)
式は,$V(x, y) = (1 - x^2 - y^2)^2 + y^2/(x^2 + y^2)$ってやつです.
以下はjupyterのセルに直接入れりゃ動くのということを意識していきますね.

ライブラリのimport

今回使うのは基本的な3つです.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

データ用意

等高線を描くためには$x$と$y$についてグリットに切って,その各点でのポテンシャル$V$を計算する必要があるのでそれを用意します.
まずはグリッドの準備.

x = np.linspace(start=-1.5, stop=1.5, num=301)
y = np.linspace(start=-.8, stop=1.5, num=231)

numpyでのリストの生成にはarangeとlinspaceがありますが,今回はlinspaceで作りました.
startからstopまでnum個に切ってねってやつです.

xとyのデータを2次元にします.

X, Y = np.meshgrid(x, y)

これが急に何すんの?って思ったやつです.イメージとしては,

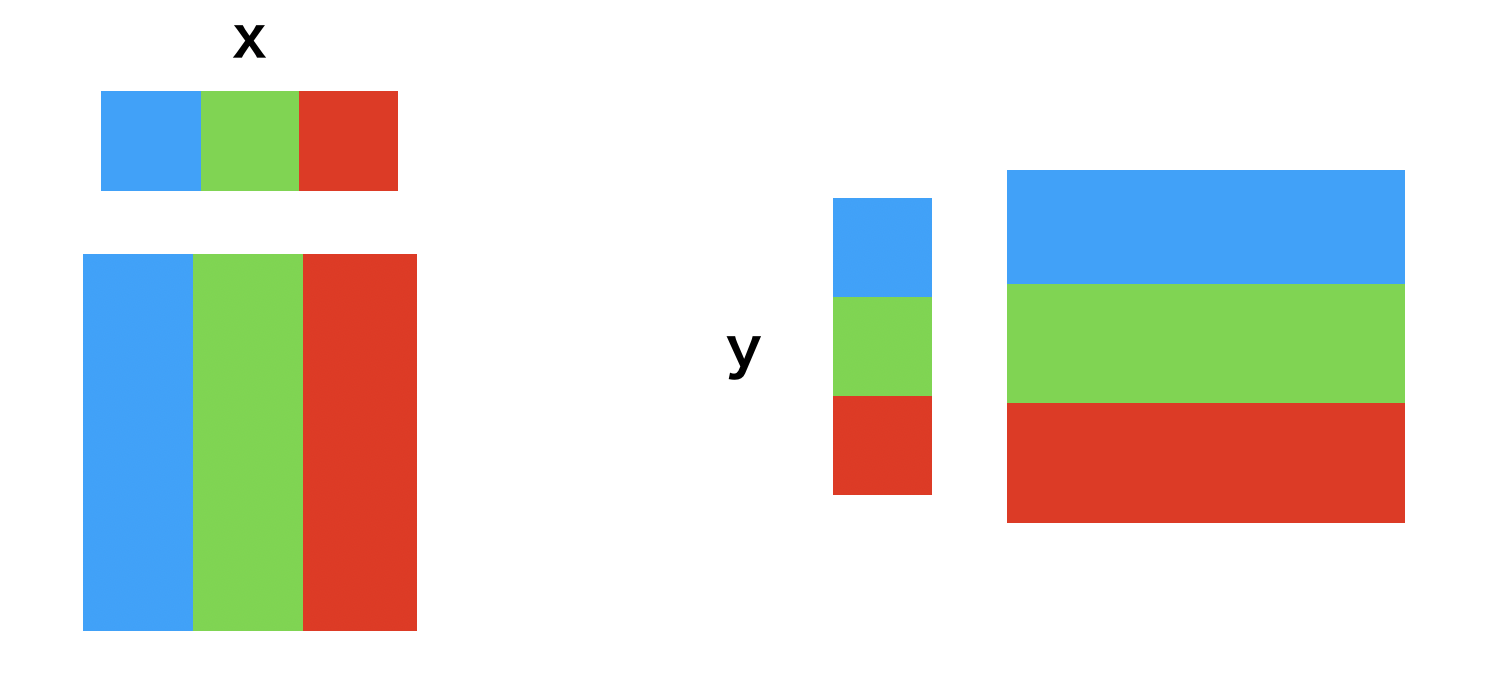
こんな風に1次元が2次元にされてる感じです.

次にポテンシャルの関数を用意します.数値でもndarrayでもどんとこいというやつにしておきます.

def get_potential(x, y):
    return (1 - x**2 - y**2)**2 + y**2/(x**2 + y**2+ 1e-10)

そしたら先程用意したグリッドからポテンシャルを計算します.

Z = get_potential(X,Y)

可視化

ここまできたらあとは可視化です.

fig, ax = plt.subplots(figsize=(15, 11.5))
ax.contour(X, Y, Z, levels=np.linspace(0, 5, 40))
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
# 保存
fig.savefig('contour.png')

完成!🎉
スクロールするとふわーんってなってきれいですね.
クリスマスっぽいですね.

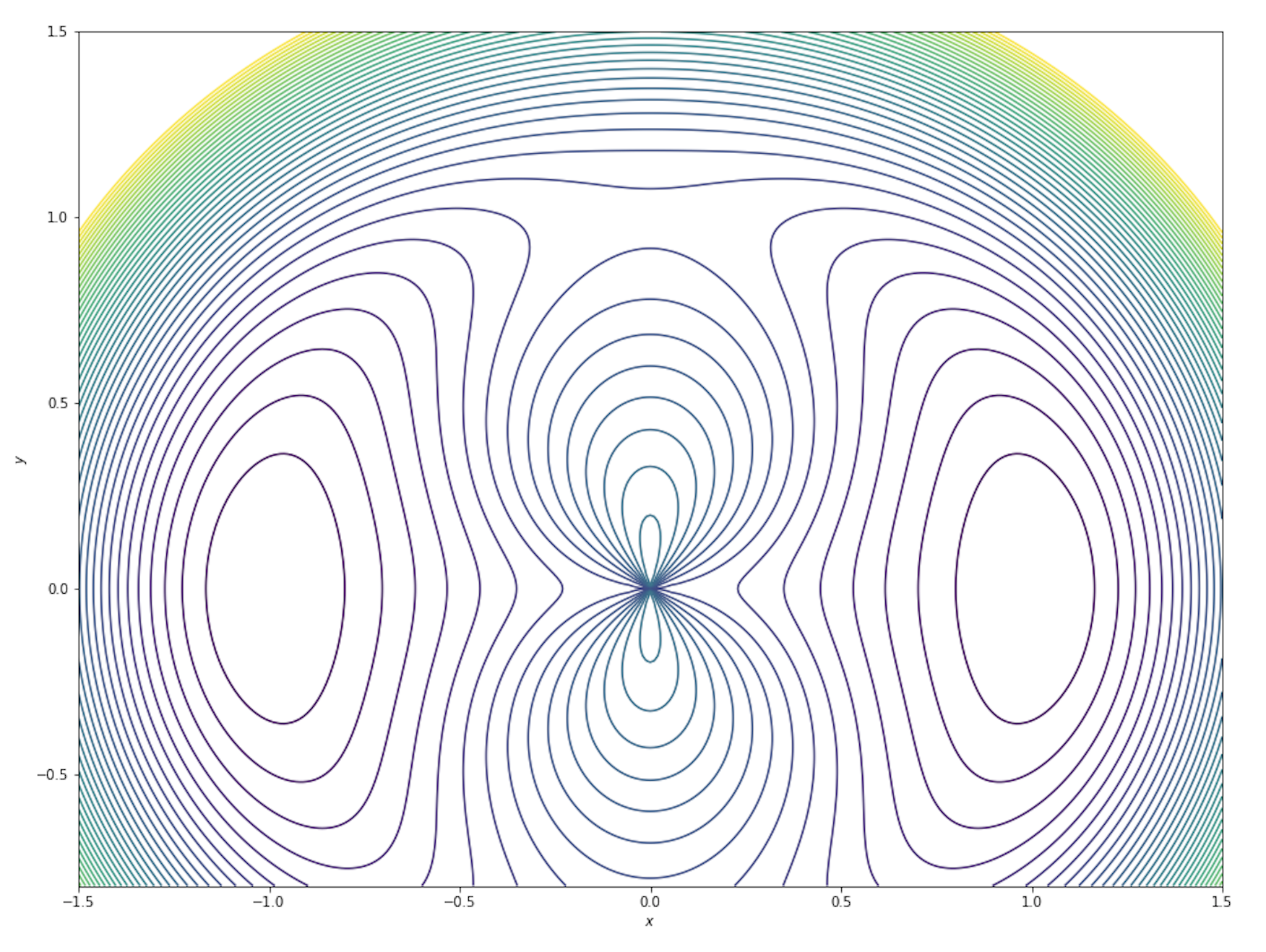
figsizeのところを調整してあげると自分が希望するアスペクト比,大きさの画像を作れます.
ax.contour()のX,Y,Zのイメージは,

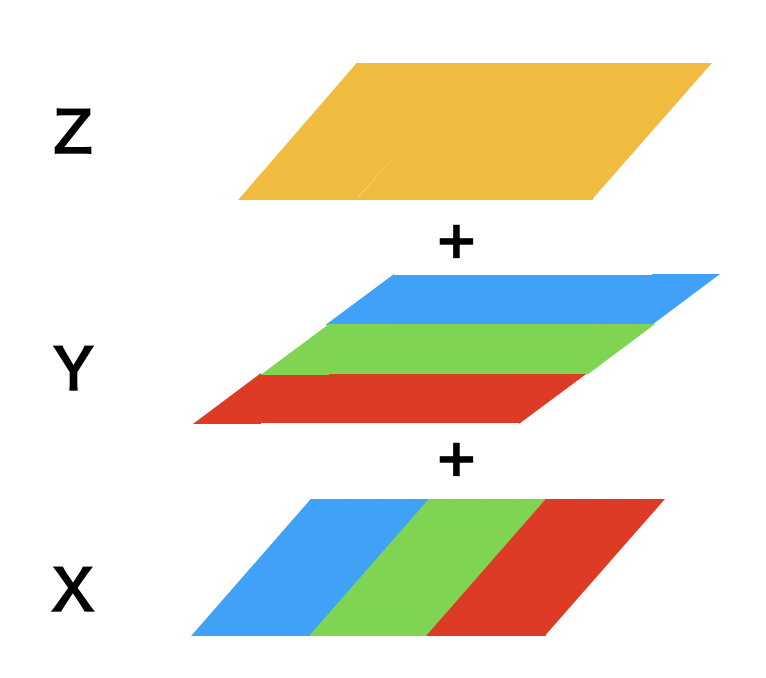
って感じです.meshgridしたありがたみとしては,グリッドが歪んでたりするデータに関してプロットしたい!とか言うときにありがたみを感じました.
levelsはリストになっていて,そのリストで指定されてる値のところに等高線が引かれるようになります.

保存

そしたら最後にデータの保存だけしようと思います.
ポテンシャルの計算にめちゃくちゃ時間がかかる場合とかありますよね.そういうときはちゃんと保存しておきたいですよね.
これを今までは謎のdatファイルとか作ってましたが,padasで行っていきたいと思います.
pandasを使って2次元のリストを1次元に直して,列名をつけて保存するだけです.

data = pd.DataFrame(
    {'x': np.reshape(X, X.shape[0]*X.shape[1]),
     'y': np.reshape(Y, Y.shape[0]*Y.shape[1]),
     'z': np.reshape(Z, Z.shape[0]*Z.shape[1])}
)

これでこんな感じのわかりやすい形式で保存されてます.

これをcsvに書き出すなら,

data.to_csv('./data.csv')

読み込むなら

data = pd.read_csv('./data.csv')

として,2次元リストのX, Y, Zを復元するなら

X = np.reshape(data['x'].values, (data['y'].nunique(), data['x'].nunique()))
Y = np.reshape(data['y'].values, (data['y'].nunique(), data['x'].nunique()))
Z = np.reshape(data['z'].values, (data['y'].nunique(), data['x'].nunique()))

とすればできますね!
これはご自身のデータに合わせる必要がありますが,numpyのAPIでやる分には自分で謎のscriptを生成するより良いかなと思います.

まとめ

なんだかこれを書くことで当時の僕が少し救われた気持ちになりました.
物理してた頃は実験結果がなんぼの世界だったので,こういうtipsを話し合ったりする場がなかったので...
なので今こういう場があることがとても幸せで,とても楽しいです!

追記

2018/12/04contourに渡す引数が間違っていたので修正しました.

大学生の僕に贈るデータ処理と可視化のお話