前書き
本記事では、Quantum Katas の Quantum Phase Estimation について解説します。Q# や Quantum Katas って何よという方は Quantum Katas で始める量子コンピュータ入門 |0⟩ をご参照ください。
さて、勝手にまとめて来た Quantum Katas のまとめの第 $|11⟩$ 段です。つい先月 Grover アルゴリズムをまとめた際に "現時点で公開されている Quantum Katas は完了" といったばかりなのですが、早速新しい Kata が追加されました。
今回は Quantum Phase Estimation アルゴリズムです。日本語だと、量子位相推定とかいうのでしょうか。量子ビットを操作するユニタリ行列はその性質上、固有値を単位円上に持ちますが、Quantum Phase Estimation ではこの固有値の位相を算出します。英語版の Wikipedia によると、quantum eigenvalue estimation algorithm (日本語だと量子固有値推定?) と呼ばれることもあるようです。
固有状態ってなによ
この Kata 全体を通して、初めて固有状態 (Eigenstate) という概念がいきなり登場します。結論から言ってしまえば、固有状態とはある基底に対して観測を行った際に、確率 1 で同じ結果が得られるような状態を指します。1 量子ビットの系で計算基底と呼ばれる Pauli Z による観測を行う場合は、$|0⟩$か$|1⟩$のことですね。
Joint Measurement でも少し出てきましたが、量子コンピューターで利用されるゲート (ユニタリ行列による演算で表記される) は物理量に相当します。また、ある基底に対する観測では基底行列の固有値が得られるのでした。要は、観測対象の状態が毎回同じ固有値が得られるよう状態である場合に、その状態は固有状態であると言われます。もっとちゃんと理解したいという方は Wikipedia の固有状態の記事 がおすすめです。
各 Task の解説
Task 1.1. Inputs to QPE: eigenstates of Z/S/T gates.
問題
入力: 量子ビット $|0\rangle$ と目標とする Z ゲートの固有状態を示す整数
ゴール: 与えられた整数が 0 なら固有状態 $|0\rangle$ を、1 なら固有状態 $|1\rangle$ を生成せよ。
解説
整数が 1 だったら反転する、というだけも問題です。これは楽勝ですね。
operation Eigenstates_ZST (q : Qubit, state : Int) : Unit {
body (...) {
if(state == 1) {
X(q);
}
}
adjoint auto;
}
Task 1.2. Inputs to QPE: powers of Z/S/T gates.
問題
入力: 1 量子ビットを処理するユニタリ オペレーター $U$ と正の整数 $\text{power}$
出力: ユニタリ オペレーター $U^{\text{power}}$ を出力せよ。
解説
ユニタリ オペレーターが与えられるので、それを $n$ 上したオペレーションを返せ、という問題です。予め用意された UnitaryPower は 量子ビットを受け取らず、function になっているので、ヒントにもある通り自分でオレペレーションを作る必要があります。Grover でもやりましたが、部分適用でクリアできそうですね。
// 自分で作成したオペレーション
operation myOwnUnit (U : (Qubit => Unit : Adjoint, Controlled), power : Int, q: Qubit) : Unit {
body(...) {
for(i in 0..power-1) {
U(q);
}
}
adjoint auto;
controlled adjoint auto;
}
// Task にもともと用意されている function
function UnitaryPower (U : (Qubit => Unit : Adjoint, Controlled), power : Int) : (Qubit => Unit : Adjoint, Controlled) {
return myOwnUnit(U, power, _);
}
元々のお題として、UnitaryPower 関数の戻り値が Unit : Adjoint, Controlled で指定されている点に注意してください。返されるオペレーション自身も Adjointable かつ Controllable である必要があるので、オペレーションには adjoint auto; などを指定しないと型の不一致によるエラーが発生します。
Task 1.3. Validate inputs to QPE
問題
入力: 1 量子ビットを処理するユニタリ オペレーター $U$ とある量子ビットの状態 $|\psi⟩ = P|0⟩$ を満たすユニタリ オペレーター $P$
ゴール: $|\psi⟩$ が $U$ の固有状態となっていない場合は例外をスローせよ。固有状態となっている場合は何もしなくてよい。
解説
かなり毛色が違う問題ですね。ただ、それほど身構える必要はありません。まず、$|\psi⟩ = P|0⟩$ なので
$$
UP|0⟩ = U|\psi⟩
$$
となることがわかります。状態 $|\psi⟩$ が $U$ の固有状態である場合は、固有値 を$\lambda$ とすると $U|\psi⟩ = \lambda|\psi⟩$ なので、さらに左から $P$ のエルミート行例である $P^*$ をかけてやると
P^{*}UP|0⟩ = P^*U|\psi⟩ = P^*\lambda|\psi⟩ = \lambda P^*|\psi⟩ = \lambda|0⟩
となることがわかります。なので、コードとしても $P$、$U$、$P^*$ の順で処理し、結果が Zero なら固有状態であることがわかります。今回の問題は固有状態以外なら例外をスローせよとあるので、Zero 以外なら例外をスローすればよさそうです。与えられた量子ビットが全て $|0⟩$ のとき以外は例外をすろーする AssertAllZero オペレーションを使えば実現できそうですね。
回答は以下になります。
operation AssertIsEigenstate (U : (Qubit => Unit), P : (Qubit => Unit : Adjoint)) : Unit {
using(qs = Qubit()) {
// P^*UP|0⟩ を計算
P(qs);
U(qs);
Adjoint P(qs);
// |0⟩ 以外なら例外をスロー
AssertAllZero([qs]);
//いつもどおり使った量子ビットはリセット
Reset(qs);
}
Task は一旦おいておいて量子位相推定とはなにか
さて、ここまでで事前準備は終了です。続いて、今回の本題の量子位相推定について説明するのですが、量子位相推定を行う際には、量子フーリエ変換が利用されます。量子フーリエ変換は離散フーリエ変換の量子ビット版です。なので、ここからは以下の順で解説します。
- 離散フーリエ変換とユニタリ行列
- 量子フーリエ変換
- 量子位相推定
1. 離散フーリエ変換とユニタリ行列
ちょっと横道にはそれますが、離散フーリエ変換とは、以下のような変換をいいます。
離散フーリエ変換
$N$ 個の離散時間信号 $\{x_n\}_{n=0}^{N-1}$ の離散フーリエ変換は
$$ X_k = \sum_{n=0}^{N-1}x_nW^{nk} $$
で定義される。また、$X_k$ から $x_n$ を計算する逆離散フーリエ変換は
$$x_n = \frac{1}{N}\sum_{k=0}^{N-1}X_kW^{-nk}$$
で与えられる。ただし、
$$W=e^{-2\pi i/N}$$
である。
信号処理をやったことがある方にとってはおなじみですね。時間領域の信号を周波数領域に変換して解析を行うための超基本的な手法です。離散フーリエ変換自体の詳細を知りたい方は Wikipediaの記事 をご参照ください。
これが量子コンピューターとどう関係があるんだ?? と思われるかもしれませんが、なんのことはありません。量子コンピューターはユニタリ変換が実行できるのでした。上記はユニタリ変換になっているでしょうか?確かめてみましょう。行列で書き下すと
\begin{bmatrix}
X_0 \\
X_1 \\
X_2 \\
\vdots \\
X_{N-1}
\end{bmatrix}
=
\begin{bmatrix}
W^0 & W^0 & W^0 & \cdots & W^0 \\
W^0 & W^1 & W^2 & \cdots & W^{N-1} \\
W^0 & W^2 & W^4 & \cdots & W^{2(N-1)} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
W^0 & W^{N-1} & W^{2(N-1)} & \cdots & W^{(N-1)^2}
\end{bmatrix}
\begin{bmatrix}
x_0 \\
x_1 \\
x_2 \\
\vdots \\
x_{N-1}
\end{bmatrix}
となるので、上記の $W$ からなる行列を $\mathbf W$ の複素共役を $\mathbf{\bar W}$ とすると
\mathbf{W\bar W} =
\begin{bmatrix}
W^0 & W^0 & W^0 & \cdots & W^0 \\
W^0 & W^1 & W^2 & \cdots & W^{N-1} \\
W^0 & W^2 & W^4 & \cdots & W^{2(N-1)} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
W^0 & W^{N-1} & W^{2(N-1)} & \cdots & W^{(N-1)^2}
\end{bmatrix}
\begin{bmatrix}
\bar W^0 & \bar W^0 & \bar W^0 & \cdots & \bar W^0 \\
\bar W^0 & \bar W^1 & \bar W^2 & \cdots & \bar W^{N-1} \\
\bar W^0 & \bar W^2 & \bar W^4 & \cdots & \bar W^{2(N-1)} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
\bar W^0 & \bar W^{N-1} & \bar W^{2(N-1)} & \cdots & \bar W^{(N-1)^2}
\end{bmatrix}
とかけます。上記より、$\mathbf{W\bar W}$ の $(n,m)$ 成分を $w_{n, m}$ とすると
$$
w_{n,m} = \sum_{k=0}^{N-1} W^{nk}\bar W^{mk} = \sum_{k=0}^{N-1} W^{nk} W^{-mk} = \sum_{k=0}^{N-1} W^{(n - m)k}
$$
となりますね。対角成分 ($m=n$) であれば上記は $N$ になることがわかります。一方対角成分以外は、高校数学で習う等比数列を思い出せば0 になることを説明できます。
$$
w_{n,m} = \sum_{k=0}^{N-1} W^{(n - m)k} = W^0 + W^{n-m} + W^{2(n-m)} + \cdots + W^{(N-1)(n-m)}
$$
で、両辺に $W^{n-m}$ をかけると
$$
W^{n-m}w_{n,m} = W^{n-m} + W^{2(n-m)} + W^{3(n-m)} + \cdots + W^{N(n-m)}
$$
なので、この2つの式の差を取ると
$$
(1- W^{n-m})w_{n,m} = W^0 - W^{N(n-m)} \Leftrightarrow w_{n,m} = \frac{W^0 - W^{N(n-m)}}{1- W^{n-m}} = \frac{1 - 1^{(n-m)}}{1- W^{n-m}} = 0
$$
となり、各成分が 0 になることがわかります。すなわち、
\mathbf{W\bar W} =
\begin{bmatrix}
N & 0 & 0 & \cdots & 0 \\
0 & N & 0 & \cdots & 0 \\
0 & 0 & N & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \cdots & N
\end{bmatrix}
です。N 倍されてしまっているのでこの時点ではユニタリ行列ではないのですが、要は $\frac{1}{\sqrt N}$ すればユニタリ変換とでき、そして量子回路で実装することができそうですね。長々と書いてきましたが、要は 離散フーリエ変換は係数を調整すればユニタリ変換にできるので、量子回路で実装可能だという点が言いたかったこととなります。
2. 量子フーリエ変換
すでに確かめたように、離散フーリエ変換は係数を調整すればユニタリ変換にできるので、量子フーリエ変換の定義は離散フーリエ変換と同じです。調べてみた感じでは、あの有名な Shor のアルゴリズムの論文 で紹介されていて、同時期に Coppersmith の論文 なんかでも論じられていたようですが、具体的に初出がどこかを確かめることはできませんでした。
量子フーリエ変換
長さ N の量子ビット $|k⟩$ の量子フーリエ変換 $\text {QFT}$ は
$$ \text{QFT}|k⟩ = \frac{1}{\sqrt N}\sum_{n=0}^{N-1}\omega^{nk}|n⟩ $$
で定義される。また、逆離散フーリエ変換は
$$ \text{QFT}^{-1}|k⟩ = \frac{1}{\sqrt N}\sum_{n=0}^{N-1}\omega^{-nk}|n⟩ $$
で与えられる。ただし、
$$\omega=e^{2\pi i/N}$$
てっきり Katas の中でまずは QFT を自分で回路としてかいてみようという話が出てくるとばかり思っていたのですが、外れでした。QFT が実際にはどう実装されるか、という点はお預けにしましょう。
3. 量子位相推定
さて、ここからが今回の主題の量子位相推定です。まずは位相ってなんの位相よという点についてですが、これはユニタリ行列の固有値の位相のことになります。ユニタリ行列はエルミート転置をかけると単位行列になる行列なので、固有値の絶対値は必ず 1 となります。
$U|\psi⟩ = \lambda|\psi⟩$ としたときに
\begin{aligned}
&(左辺)^2 = |U|\psi⟩|^2 = \overline{(U|\psi⟩)} U|\psi⟩ = \langle \psi | \overline U U |\psi⟩ = \langle \psi |\psi⟩ \\
&(右辺)^2 = |\lambda|^2 \langle \psi |\psi⟩
\end{aligned}
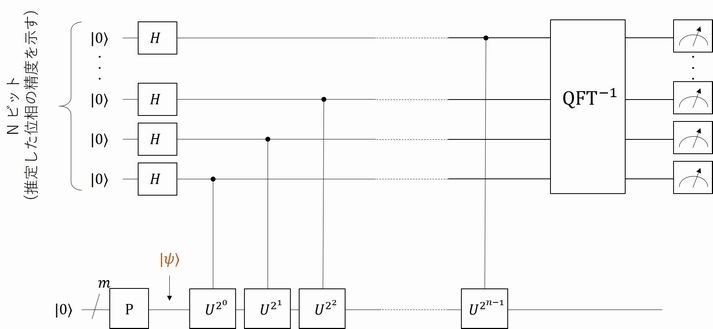
からも確かめられます。固有値の絶対値が 1 ということは、単位円上に固有値が存在するということになるので、固有値は任意の位相 $\theta$ を用いて $\lambda = e^{2\pi i \theta}$ (ここで、$\theta \in [0, 1) です$) と置き換えられます。これが、このアルゴリズムが位相推定と呼ばれたり固有値推定と呼ばれたりする所以です。ユニタリ変換の固有値を求めることは、位相を求めることなのだと理解できた所で、今回の回答の回路図をお見せしましょう。
いつもどおり、回路としてはスッキリしていますね。また、前回やった Grover のように複雑な計算もなく、繰り返しなども必要なさそうです。実際、計算もそれほど複雑ではないので割とサクッと確かめることが可能です。
まずは最初の Controlled ゲートについて確かめてみましょう。制御ビットはアダマールゲートで処理されているのでいつもの $\frac{1}{\sqrt 2}(|0⟩ + |1⟩)$ で、ターゲットは $|\psi⟩$ なので、$U$ で処理される前は
$$
\frac{1}{\sqrt 2}(|0⟩ + |1⟩)|\psi⟩
$$
と記述されます。これをゲートで処理すると、$U|\psi⟩ = e^{2\pi i \theta}|\psi⟩$ に注意すると、
$$
\frac{1}{\sqrt 2}(|0⟩ + e^{2\pi i \theta}|1⟩)|\psi⟩
$$
と記述でき、状態 $|1⟩$ の位相として固有値が乗ることがわかります。これまでのアルゴリズムでもやってきたとおり、情報さえ取り出せれば最終ビットは捨ててしまって問題なく、QFT への入力は$\frac{1}{\sqrt 2}(|0⟩ + e^{2\pi i \theta}|1⟩)$ となります。同じように考えていくと、上位 N ビットを $|x⟩$ とおくと
\begin{aligned}
|x⟩
&=
\frac{1}{\sqrt 2}(|0⟩ + e^{2\pi i 2^{n-1}\theta}|1⟩) \otimes
\frac{1}{\sqrt 2}(|0⟩ + e^{2\pi i 2^{n-2}\theta}|1⟩) \otimes
\cdots \otimes
\frac{1}{\sqrt 2}(|0⟩ + e^{2\pi i 2^1\theta}|1⟩) \otimes
\frac{1}{\sqrt 2}(|0⟩ + e^{2\pi i \theta}|1⟩) \\
&=
\frac{1}{\sqrt N}\big((|0⟩ + e^{2\pi i 2^{n-1}\theta}|1⟩) \otimes
(|0⟩ + e^{2\pi i 2^{n-2}\theta}|1⟩) \otimes
\cdots \otimes
(|0⟩ + e^{2\pi i 2^1\theta}|1⟩) \otimes
(|0⟩ + e^{2\pi i \theta}|1⟩)\big)
\end{aligned}
となります。$U$ によって生じた $2^{j-1}$ が $e$ の肩に乗っていて邪魔っぽく見えますが、実はそんなことないのです(だから上記では先頭の 2 を残しています)。2 進数に慣れ親しんだ方ならピンと来るかもしれませんが、まさに上記の $2^{j-1}$ は対象のビットが 1 のときの 10 進数の値を示しているのです。例えば 4 量子ビットで状態が $|1000⟩$ とすると $e^{2\pi i 2^3\theta} = e^{2\pi i 8\theta}$ となります。同様に $|1010⟩$ とすると位相は $e^{2\pi i 2^3\theta}e^{2\pi i 2^1\theta} = e^{2\pi i 10\theta}$ となります。要は、量子ビットの値が肩に乗る、ということです。なんと簡単な! という感じですが、上記の QFT の入力は以下のように書けることがわかります。
\begin{aligned}
|x⟩
&=
\frac{1}{\sqrt N}\big((|0⟩ + e^{2\pi i 2^{n-1}\theta}|1⟩) \otimes
(|0⟩ + e^{2\pi i 2^{n-2}\theta}|1⟩) \otimes
\cdots \otimes
(|0⟩ + e^{2\pi i 2^1\theta}|1⟩) \otimes
(|0⟩ + e^{2\pi i \theta}|1⟩)\big) \\
&=
\frac{1}{\sqrt N}\sum_{k=0}^{N-1} e^{2\pi i k\theta}|k⟩
\end{aligned}
さて、先に示した量子フーリエ変換の定義を、できるだけ上記の変数に合うように書いてやると
$$
\text{QFT}|\theta⟩ = \frac{1}{\sqrt N}\sum_{k=0}^{N-1}e^{2\pi ik \theta/N}|k⟩
$$
となることがわかります。ほぼそのまんまですね。上記は QFT なので、右辺を逆 QFT すれば左辺の $\theta$ に戻るはずです。なので、逆 QFT の結果としていかが得られます。
$$
\text{QFT}^{-1}|x⟩ = \text{QFT}^{-1}\left( \frac{1}{\sqrt N}\sum_{k=0}^{N-1} e^{2\pi i k\theta}|k⟩ \right) = |{N\theta}\rangle
$$
要は、求めたかった $\theta$ を $N$ 倍したものが得られることがわかります。$\theta \in [0, 1)$ でしたから、小数で表される位相を N 倍して、実数で出力してくれるとも言えますね。なので、出てきた値を N で割ってやれば、求めたかった位相 $\theta$ を得ることができます。やったー!
ウソつけと思った方へ
$N\theta$ が整数にならない場合は上記の式は成り立たないので、そんなうまくいくわけ無いだろ嘘つくなと思った方、正解です。しかしながら、実際に $N\theta$ が整数にならない場合も上記のアルゴリズムで近似値を求められることが示されています。気分が乗ったら (もしくは Task が追加されたら) 追記するかもしれませんが、詳しく知りたい方は以下辺りを見てみてください。
余談ですが上記の物理とかも素晴らしいサイトですねえ。。。
というわけでとりあえず Task の解説に戻ります。
Task の解説続き
Task 1.4 QPE for single-qubit unitaries
問題
入力: 1 量子ビットのオペレーター $U$、$U$ の固有状態 $|\psi\rangle$ を生成するオペレーター $P$ (言い換えると $P|0⟩ = |\psi\rangle$)、整数 $n$
出力: 与えられたオペレーター $U$ の固有値の位相を $n$ ビットの精度で出力せよ。
解説
ここまでの原理がわかれば、あとは実装するだけですね。特につまづきポイントもないかと思います。
operation QPE (U : (Qubit => Unit : Adjoint, Controlled), P : (Qubit => Unit : Adjoint), n : Int) : Double {
// 結果を初期化
mutable resultD = -1.0;
// 今回はオペレーターが 1 量子ビットで精度が n なので、n+1 ビットを用意
using(qubits = Qubit[n+1]) {
let qs = qubits[0..n-1];
let target = qubits[n];
// P で処理して固有状態を生成
P(target);
// アダマールゲートで処理
ApplyToEach(H, qs);
// Task 1.3 で作成した U^n を適用するオペレーションを Controlled 付きで使用
for(i in 0..n-1) {
(Controlled myOwnUnit)([qs[n-1-i]],( U, 2^(i), target));
}
// 逆 QFT を実施
Adjoint QFT(BigEndian(qs));
// 結果を Int で観測
let result = MeasureIntegerBE(BigEndian(qs));
// サイズ N で割って \theta を得る
set resultD = ToDouble(result)/PowD(2.0, ToDouble(n));
ResetAll(qubits);
}
return resultD;
}
そしてあとから知ったのですが、Q# には QuantumPhaseEstimation なんていうオペレーションがそもそも存在しています。引数が DiscreteOracle 型 (Int と Qubit を渡せば $U^n$ を実行するオラクル) となっている点に注意が必要です。まあ上記の十分シンプルなので良しとしましょう。
続いては Phase Estimation の改良です
いやーちゃんと位相推定できましたね、めでたしめでたし…と行きたいところなのですが、この Kata はまだ終わりません。続いては、上記の位相推定アルゴリズムの改良版の触りを学びます。
改良版が着目したのは、主に必要となる量子ビットの数です。上記の解説からも明らかなとおり、量子位相推定では本来必要となる量子ビットに加え、推定対象の位相の精度 $n$ に応じた余分な量子ビットが必要となります。先ほどの Task でいえば、推定対象の量子ビットは 1 量子ビットなのに、その位相を推定するために $n$ ビットを使っていました。現時点では量子ビットの数も限られますし、正直現実的な方法とはいいがたいです。
そこで、少ない量子ビットで繰り返し処理を行い、位相推定を行おうという考えに基づいたアルゴリズムが提案されました。あくまで触りなので全体概要のような理論の説明は含まれません。
あまりピンと来ないかもしれませんが、やっていくと意味がわかるかなと思いますので、とりあえず進めていきます。
Task 2.1. Single-bit phase estimation
問題
入力: 固有値が $1$ もしくは $-1$ (言い換えると、位相が 0 もしくは 0.5) であることが保証された 1 量子ビットのオペレーター $U$ と、$U$ の固有状態 $|\psi\rangle$ を生成するオペレーター $P$
出力: 与えられたオペレーター $U$ の固有値を Int で出力せよ。ただし、量子ビットは高々2つしか使ってはならない。
解説
難しい位相推定を行った後だと難しい問題かと気構えますが、この問題は本当に大したことありません。与えられた $U$ の固有値は $\pm 1$ のどちらかなので、アダマールゲートで処理した量子ビットを制御ビットとして Controlled U で処理すれば位相が変化しますので、観測結果が 0 か 1 かで判別ができそうです。回答は以下です。
operation SingleBitPE (U : (Qubit => Unit : Adjoint, Controlled), P : (Qubit => Unit : Adjoint)) : Int {
mutable result = 0;
using(qs = Qubit[2]) {
let ctrl = qs[0];
let trgt = qs[1];
P(trgt);
H(ctrl);
(Controlled U)([ctrl], trgt);
H(ctrl);
if(M(ctrl) == Zero) {
set result = 1;
} else {
set result = -1;
}
ResetAll(qs);
}
return result;
}
これは問題が単純過ぎて意味がわからないかもしれませんが、次に行きましょう。
Task 2.2. Two bit phase estimation
問題
入力: 固有値が $1$、$i$、$-1$ もしくは $-i$ (言い換えると、位相が 0, 0.25, 0,5 もしくは 0.75) であることが保証された 1 量子ビットのオペレーター $U$ と、$U$ の固有状態 $|\psi\rangle$ を生成するオペレーター $P$
出力: 与えられたオペレーター $U$ の位相を double で出力せよ。ただし、量子ビットは高々2つしか使ってはならない。また、回答の精度は誤り率を 0.001 未満とすること。
解説
さて、先程とあまり変わらないようにも見えますが、今回は 4 つの状態を判別する必要があります。私達は観測によって $|0⟩$ か $|1⟩$ かを判別できるので、4 状態を判別するためには $\log_2 4 = 2$ ビット必要そうに思えます。1 ビットが固有状態に利用されるとすると残りは 1 ビットですが、この問題は合計 2 ビットの利用しか許容されていません。
これを解決するのが Iterative Pahse Estimation (反復位相推定 とか言うんでしょうか) になります。具体的な処理手順は Task のヒントにも記載されていますが、以下の通りです。
- Task 2.1 の内容を使って、0 か 0.5 かを区別する処理を実施する。(0.25 か 0.75 の場合は、見分けがつかない。)
- Task 2.1 の内容を修正して、0.25 か 0.75 かを区別する処理を実施する。(0 か 0.5 の場合は見分けがつかない。)
- 上記の処理を何度も繰り返し実行し、一番確率高く観測された値を位相として出力する
複数ビットを用意する代わりに、何度も処理と観測を繰り返し行うことで位相推定を行うのが Iterative Phase Estimation です。NISQ の時代でも実行できる回路規模にできそうですね。今回は都合のよい問題なので、固有値が $\pm i$ のときに Task 2.1 の回路を適用すると、ちょうど確率は 0.5 になります。また、逆に$\pm i$ を区別するためには $S$ ゲートを使えば良さそうですが、このときも固有値が $\pm 1$ なら確率はちょうど 0.5 になります。$0.5^{10} = 0.00097656\dots$ なので、10 回観測すれば誤り率は 0.001 程度にできそうです。
というわけで回答は以下になります。
operation TwoBitPE (U : (Qubit => Unit : Adjoint, Controlled), P : (Qubit => Unit : Adjoint)) : Double {
// 観測結果を格納する配列
mutable result = [0,0,0,0];
//問題文通り 2 量子ビットを確保
using(qs = Qubit[2]) {
let ctrl = qs[0];
let trgt = qs[1];
for(i in 1..10) {
// Task 2.1 そのまま
// 1 or -1 は見分けられるが、i or -i の場合は見分けられない
ResetAll(qs);
P(trgt);
H(ctrl);
(Controlled U)([ctrl], trgt);
H(ctrl);
// 観測を行った結果を代入
if(M(ctrl) == Zero) {
set result[0] = result[0] + 1;
} else {
set result[1] = result[1] + 1;
}
// 続いて i or -i を見分ける処理
ResetAll(qs);
P(trgt);
H(ctrl);
S(ctrl);
(Controlled U)([ctrl], trgt);
H(ctrl);
// 観測を行った結果を代入
if(M(ctrl) == One) {
set result[2] = result[2] + 1;
} else {
set result[3] = result[3] + 1;
}
}
ResetAll(qs);
}
// 観測結果に応じた return を実施
if(result[0] == 10) {
return 0.0;
} elif(result[1] == 10) {
return 0.5;
} elif(result[2] == 10) {
return 0.25;
} else {
return 0.75;
}
}
このあと、to be continued... という記載があるので、まだこの Kata は続きそうですね☆ミ
まとめ
今回は量子位相推定について学びました。先人たちが残した結果を着々と学んで行けている感じがして最高ですね。まだこの Kata は続きそうですし、Kata で紹介されている論文 にも様々な手法が紹介されているので、他の位相推定手法とのメリット/デメリット比較なんかもでてくるのかなと思います。とりあえず現時点ではここまでで。