Go to Qiita Advent Calendar 2024 Top
LoginSignup
4
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@tehishik

Quantum Katas で始める量子コンピュータ入門 |8⟩: Joint Measurement

Posted at

前書き

本記事では、Quantum Katas の Mesurement について解説します。Q# や Quantum Katas って何よという方は Quantum Katas で始める量子コンピュータ入門 |0⟩ をご参照ください。

今回の Kata は Joint Measurement です。すでに|3⟩: Measuerment にて観測について学びましたが、Measurement では単一量子ビットを、Pauli Z 基底に対して行う観測のみ実施しました。今回は様々な量子状態の観測方法を学び、量子現象の観測の奥深さと Q# での観測の記述方法を学んでいきます。

また、この Kata は個人的には死ぬほどとっつきにくいと思います。サイモンのアルゴリズムのような数学的な難しさではないのですが、私のような素人には非常にハードルの高い Task でした。。。始める前に、今回は Born の確率規則から紹介します。

Born の確率規則

ある物理量 $\mathbf A$ が N 個の固有値 $\lambda_i$ ($0 \le i \le N$) をもつとする。このとき、状態 $|\psi⟩$ のもとで物理量 $\mathbf A$ を観測したときに、固有値 $\lambda_i$ が観測される確率は、
$$\Pr(\mathbf A | \psi⟩) = {\displaystyle \langle \psi |P_{i}|\psi \rangle }$$
で表される。ただし、$P_i$ は $\mathbf A$ の固有値 $\lambda_i$ に対する固有射影演算子である。

また、物理量 $\mathbf A$ が $l$ 個の独立な固有値を持つ場合、それぞれの固有値 $\lambda_i$ に対する固有ベクトル $|\phi_i⟩$ は直行するため、固有射影演算子 $P_i$ は $P_i = \sum_{k = 1}^{l} |\phi_{i, k}\rangle \langle \phi_{i, k}|$ とかけるため、Born の確率規則は
$$\Pr(\mathbf A | \psi⟩) = {\displaystyle \langle \psi |P_{i}|\psi \rangle } = \sum_{k = 1}^{l} |\langle \phi_{i, k}|\psi \rangle |^2$$
と書ける。

難しそうなことを言っていますが、難しいです。正直実感としてよくわからないんですよねー。観測対象となる波動関数 $|\psi \rangle$ は、古典ビットのように 0 か 1 かのように区別できないだけでなく、状態が重ね合わされているうえ、重ね合わせた状態をまとめて観測すると、物理量の固有値が観測されるそうです。また、上記の観測の場合はこれまでのようなブロッホ球上の量子ビットの状態を想像するという手法が通用しません（多分）。

また、上記の Born の確率規則にあるような複数量子ビットに対する一般的な観測を Q# で行う場合は、Measure operation が利用できます。M オペレーションの引数は量子ビットでしたが、Measure の引数は量子ビットに加え、観測を行う基底が与えられる点に注意してください。

ちょっと話はそれますが、じゃあこれまでにやってきた単一量子ビットの観測と上記の Born の確率規則の整合性はとれているのかという点が気になるかと思います。当たり前かもしれませんが、取れているのです。Q# の M operation のページ では、このオペレーションが

  • パウリの Z 基底にて単一量子ビットを観測する操作を行うこと
  • 固有値 +1 が観測されたときに Zero を、固有値 -1 が観測されたときに One を返すこと

がそれぞれ紹介されています。Born の確率規則を知るまでは固有値ってなんの固有値だよって感じではあったのですが、これは観測を行う物理演算 (M オペレーションの場合はパウリの Z) が相当します。

\sigma_z = 
\begin{pmatrix}
    1 & 0 \\
    0 & -1  
\end{pmatrix}

より、この行列は明らかに固有値として $\pm 1$ を持ちます。また、固有方程式から

  • 固有値が +1 のときは、固有ベクトルが $(1, 0)^T = |0⟩$ となる
  • 固有値が -1 のときは、固有ベクトルが $(1, 0)^T = |1⟩$ となる

となることもわかります。こんなふうに 1 量子ビットの観測ならことは単純なのですが、複数の基底に対する観測を行うときは十分に注意が必要ですねえ。。。

周り道をしましたが、Task の解説に進みます。

各 Task の解説

Task 1. Single-qubit measurement

問題

入力: 2 つのもつれ合わせ状態にある量子ビット。ただし、$|00⟩$ と $|11⟩$ の重ね合わせか、$|01⟩$ と $|10⟩$ の重ね合わせ状態のどちらかにあるとする。

出力: 一つ目に記載された重ね合わせ状態が観測された場合は 0 を、二つ目に記載された重ね合わせ状態が観測された場合は 1 を出力せよ。オペレーション終了後の量子ビットの状態は問わない。

解説

まずは練習のタスクです。複数の量子ビットを個別に M オペレーションで観測する場合は、観測後に量子ビットの状態が保たれません。ですが、今回の問題ではオペレーション後の量子ビットの状態はどうでもいいとのことなので、これまで通り M オペレーションで観測した結果が一致するかどうかで判定すればよさそうです。回答は以下。

operation SingleQubitMeasurement (qs : Qubit[]) : Int {
    if(M(qs[0]) == M(qs[1])) {
        return 0;
    }
    else {
        return 1;
    }
}

これは単純ですね。

Task 2 Parity measurement

問題

入力: 2 つのもつれ合わせ状態にある量子ビット。ただし、$|00⟩$ と $|11⟩$ の重ね合わせか、$|01⟩$ と $|10⟩$ の重ね合わせ状態のどちらかにあるとする。

出力: 一つ目に記載された重ね合わせ状態が観測された場合は 0 を、二つ目に記載された重ね合わせ状態が観測された場合は 1 を出力せよ。ただし、オペレーション終了後の量子ビットは初期状態と同じでなくてはならない。

解説

観測すべき条件や返却すべき値は先のタスクと全く同じなのですが、状態を壊すなという点だけが異なります。M オペレーションを実行すると量子ビットの状態が定まってしまうので、それぞれ観測する方法は使えません。
与えられた量子ビットの状態を触らなければいいので、アンシラビットを用意して、各量子ビットを反転しながら Controlled X で反転しつつ、状態を戻してやれば初期状態を維持できそうです。

// 間違っていないけど今回の期待する回答ではない例
operation ParityMeasurement (qs : Qubit[]) : Int {
	body(...) {
        mutable result = Zero;
        using (q = Qubit[1]) {
            // 11 ならアンシラを 1 に
            (Controlled X)(qs, q[0]);

            // 反転
            X(qs[0]);
            X(qs[1]);

            // 11 ならアンシラを 1 に （初期状態が 00 ならアンシラを 1 に）
            (Controlled X)(qs, q[0]);

            // もとに戻すために反転
            X(qs[0]);
            X(qs[1]);

            // アンシラを観測
            set result = M(q[0]);
            Reset(q[0]);
        }
        if(result == One) {
            return 0;
        }
        else {
            return 1;
        }
    }
}

上記でも回答としては間違っているわけでなく、テストとしても通るのですが、この問題はそういう問題ではありません。Joint Measurement によって上記がどのようにかけるのか、を学ぶ問題なのです。

これは試行錯誤して導き出すというよりは、ドイチェ・ジョザのアルゴリズム等と同じく先人に学ぶ必要がある内容だと思うのですが、結論から言ってしまうと Pauli の Z 基底のテンソル積として定義される $\sigma_Z \otimes \sigma_Z$ を利用すると、今回のような重ね合わせ状態を判定することが可能となります。少し計算してみましょう。

まず、上記のテンソル積は

\sigma_Z \otimes \sigma_Z = 
\begin{pmatrix}
    1 & 0 & 0 & 0 \\
    0 & -1 & 0 & 0 \\ 
    0 & 0  & -1 & 0 \\ 
    0 & 0  & 0 & 1
\end{pmatrix}

となるため、固有値として $\pm 1$ を持ちます。また、固有方程式から

  • 固有値が +1 のときは、固有ベクトルが $\frac{1}{\sqrt 2}(1, 0, 0, 1)^T$ となる
  • 固有値が -1 のときは、固有ベクトルが $\frac{1}{\sqrt 2}(0, 1, 1, 0)^T$ となる

ということがわかります。まさに今回区別したかった状態の区別が $\sigma_Z \otimes \sigma_Z$ によって行えそうですね。というわけで回答は以下となります。

operation ParityMeasurement (qs : Qubit[]) : Int {
    body(...) {
        let result = Measure([PauliZ, PauliZ], qs);
        if(result == Zero) {
            return 0;
        }else {
            return 1;
        }
    }
}

0 と 1 が一致しているかどうかを判定できるという意味で、Parity measurement と呼ばれるようです。同じかどうかは $\sigma_Z \otimes \sigma_Z$ で判定できると覚えておきましょう。

Task 3. |0000⟩ + |1111⟩ or |0011⟩ + |1100⟩ ?

問題

入力: 2 つのもつれ合わせ状態にある量子ビット。ただし、$|0000⟩$ と $|1111⟩$ の重ね合わせか、$|0011⟩$ と $|1100⟩$ の重ね合わせ状態のどちらかにあるとする。

出力: 一つ目に記載された重ね合わせ状態が観測された場合は 0 を、二つ目に記載された重ね合わせ状態が観測された場合は 1 を出力せよ。ただし、オペレーション終了後の量子ビットは初期状態と同じでなくてはならない。

解説

この問題は、2 ビット目と 3 ビット目に着目することですぐに回答することが可能です。先の Task そのままですね。

operation GHZOrGHZWithX (qs : Qubit[]) : Int {
    body(...) {
        let q = qs[1..2];
        let a = Measure([PauliZ, PauliZ], q);
        if(a == Zero) {
            return 0;
        }else {
            return 1;
        }
    }
}

Task 4. |0..0⟩ + |1..1⟩ or W state ?

問題

入力: 2 つのもつれ合わせ状態にある量子ビット。ただし、$|00\dots00⟩$ と $|11\dots11⟩$ の重ね合わせか、W 状態かのどちらかにあるとする。また、ビット数は偶数とする。

出力: W 状態なら 0 を、そうでなければ 1 を出力せよ。ただし、オペレーション終了後の量子ビットは初期状態と同じでなくてはならない。

解説

続いての問題は W 状態かどうかを見定めるという問題です。Mesurement でも似たような問題をやりましたね。今回は、Joint Measurement を使ってこの問題に取り組みます。

直前の Task では、$\sigma_Z \otimes \sigma_Z$ を使って観測を行いましたが、これを $n$ 乗積に拡張するとどうなるか考えましょう。地道に 3 乗を考えてみると

\sigma_Z^{\otimes 2} \otimes \sigma_Z = 
\begin{pmatrix}
    \sigma_Z^{\otimes 2} & 0 \\
    0 & -\sigma_Z^{\otimes 2}
\end{pmatrix}
=
\begin{pmatrix}
    1 & 0 & 0 & 0  & 0 & 0  & 0 & 0\\
    0 & -1 & 0 & 0  & 0 & 0  & 0 & 0\\ 
    0 & 0  & -1 & 0  & 0 & 0  & 0 & 0\\ 
    0 & 0  & 0 & 1 & 0 & 0  & 0 & 0\\
    0 & 0  & 0 & 0 & -1 & 0 & 0 & 0 \\
    0 & 0  & 0 & 0 & 0 & 1 & 0 & 0 \\ 
    0 & 0  & 0 & 0 & 0 & 0  & 1 & 0 \\ 
    0 & 0  & 0 & 0 & 0 & 0  & 0 & -1
\end{pmatrix}

となります。固有値 1 のときの固有ベクトルは $\frac{1}{2}(1, 0, 0, 1, 0, 1, 1, 0)^T$ となります。ちょうど $|1⟩$ が偶数個あるとき ($|000⟩$,$|011⟩$, $|101⟩$, $|110⟩$ ) だけが観測されることがわかりますね。

続いて一般化ですが、上記の結果は $n$ 乗でも変わりません。テンソル積の定義から、

\sigma_Z^{\otimes n+1} = \sigma_Z \otimes \sigma_Z^{\otimes n} = 
\begin{pmatrix}
    \sigma_Z^{\otimes n} & 0 \\
    0 & -\sigma_Z^{\otimes n}
\end{pmatrix}

となるので、行列の上半分の固有値は $\sigma_Z^{\otimes n}$ と同じで、下半分は反転していることがわかります。そのため、$\sigma_Z^{\otimes n}$ の固有値が $a$ のときの固有ベクトルを $|\psi_{a, n}⟩$ とすると

 |\psi_{1, n+1}⟩ = 
 \begin{pmatrix}
    |\psi_{1, n}⟩ \\
    |\psi_{-1, n}⟩
\end{pmatrix}

と記述できます。最初の $2^n$ 個の要素はそのまま、残りの $2^n$ 個の要素が反転している状況です。なので、$|\psi_{1, n}⟩$ が "長さ $n$ の量子ビットのうち、$|1⟩$ が偶数個ある場合のみに観測される" という性質を持つ場合は、長さ $n+1$ の量子ビットの前半 $2^{n}$ 個のについても同じ性質を持ちそうです。後半の要素は反転していますが、$|\psi_{-1, n}⟩$ が "長さ $n$ の量子ビットのうち、$|1⟩$ が奇数個ある場合のみに観測される" という性質を持つ場合は、こちらも長さ $n+1$ の量子ビットは$|1⟩$ が偶数個ある場合のみに観測されると言えそうです。（最上位ビットが $|1⟩$ となる点に注意してください）

さて、長々と書いてきましたが、今回の Task では与えられた量子ビットが$|00\dots00⟩$ と $|11\dots11⟩$ の重ね合わせか、W 状態かのどちらかを判別したいのでした。そして、量子ビットの長さは偶数なのでした。もうお分かりかと思いますが、$\sigma_Z^{\otimes n}$ に対する観測を行えば、前半の重ね合わせの場合は 1 が、W 状態なら 0 がそれぞれ出力されます。これだけで判別が可能なんですね。かつ、Q# には MeasureAllZ という $\sigma_Z^{\otimes n}$ の観測を行うオペレーションが用意されています。回答は以下となります。

operation GHZOrWState (qs : Qubit[]) : Int {
    body(...) {
        let result = MeasureAllZ(qs);
        if(result == Zero) {
            return 0;
        } else {
            return 1;
        }

    }
}

Task 5. Parity measurement in different basis

問題

入力: $\alpha|00⟩ + \beta|01⟩ + \beta|10⟩ + \alpha|11⟩$ か $\alpha|00⟩ - \beta|01⟩ + \beta|10⟩ - \alpha|11⟩$ である量子ビット

出力: 前者の重ね合わせ状態である場合は 0 を、後者の場合は 1 を出力せよ。

解説

もうこの辺は知っているか知らないかだけの問題な気もしますが、結論から言えばこの問題は $\sigma_X^{\otimes 2}$ で観測すれば回答を得ることが可能です。

\sigma_X \otimes \sigma_X = 
\begin{pmatrix}
    0 & 0 & 0 & 1 \\
    0 & 0 & 1 & 0 \\ 
    0 & 1 & 0 & 0 \\ 
    1 & 0 & 0 & 0
\end{pmatrix}

上記から固有方程式は $\lambda^4 = 1$ となるので、固有値は $\lambda = \pm 1$ です。それぞれの固有ベクトル$|\phi_{\pm 1}⟩$は

\begin{pmatrix}
    -1 & 0 & 0 & 1 \\
    0 & -1 & 1 & 0 \\ 
    0 & 1 & -1 & 0 \\ 
    1 & 0 & 0 & -1
\end{pmatrix}
\begin{pmatrix}
    a_1\\
    a_2\\
    a_3\\
    a_4
\end{pmatrix}
=
\mathbf 0

\Leftrightarrow

|\phi_1⟩ = k
\begin{pmatrix}
    a_1\\
    a_2\\
    a_2\\
    a_1
\end{pmatrix} \\

\begin{pmatrix}
    1 & 0 & 0 & 1 \\
    0 & 1 & 1 & 0 \\ 
    0 & 1 & 1 & 0 \\ 
    1 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
    a_1\\
    a_2\\
    a_3\\
    a_4
\end{pmatrix}
=
\mathbf 0

\Leftrightarrow

|\phi_{-1}⟩ = k
\begin{pmatrix}
    a_1\\
    -a_3\\
    a_3\\
    -a_1
\end{pmatrix} \\

となります。このタスクそのまんまですね。回答は以下です。

operation DifferentBasis (qs : Qubit[]) : Int {
    body(...) {
        let result = Measure([PauliX, PauliX], qs);
        if(result == Zero ) {
            return 0;
        } else {
            return 1;
        }
    }
}

Task

問題

入力: $|\psi⟩ = \alpha|0⟩ + \beta|1⟩$ と $|0⟩$ 状態の 2 つの量子ビット。2 つの量子ビットは量子もつれ状態にはない。

ゴール: 量子ビットの状態を $\alpha|00⟩ + \beta|11⟩$ に変更せよ。ただし、2 量子ゲートを使ってはならない。

解説

CNOT ゲートを使えば終了な問題かと思いきや、2 量子ゲートは使ってはいけないという制限があります。なんでこんな問題があるかといえば、トポロジカル量子ビットによる量子コンピューティングを実現するうえでは 2 量子ゲートを誤り率低く実現することが難しいからだそうです。

上記の論文にもありますが、アンシラ ビットをアダマールゲートで処理してから PauliZ で Parity Measurement を行えば CNOT ゲートが実現できるようです。回答は以下となります。

    operation ControlledX (qs : Qubit[]) : Unit {
        H(qs[1]);
		if(Measure([PauliZ, PauliZ], qs) == One) {
			X(qs[1]);
		}
    }

Task 7*. Controlled X gate with arbitrary target

問題

入力: $\alpha|00⟩ + \beta|01⟩ + \gamma|10⟩ + \delta|11⟩$ 状態にある量子ビット

ゴール: $\alpha|00⟩ + \beta|01⟩ + \delta|10⟩ + \gamma|11⟩$ 状態に変更せよ。ただし、2 量子ゲートを使ってはならない。

解説

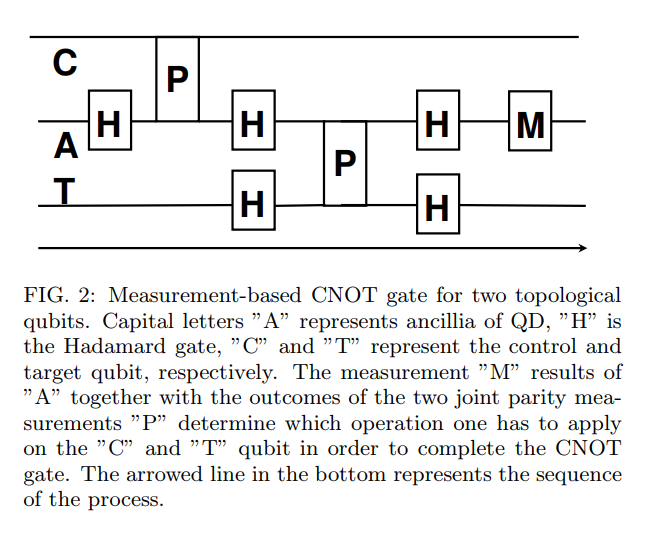
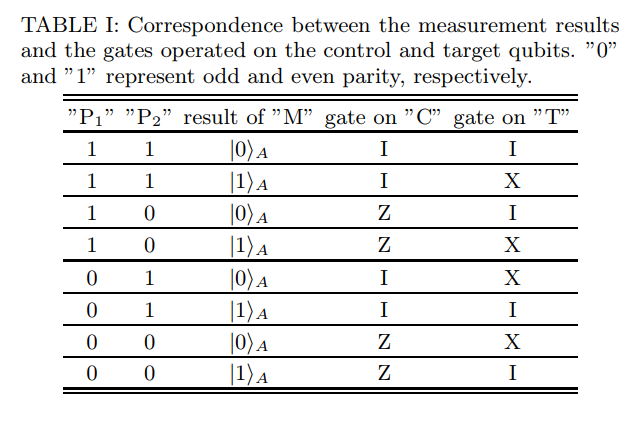
さっきの問題の亜種ですが、多分普通の人が考えて思いつくものではありません。おとなしく、Measurement based Controlled Not gate for topological qubits in a Majorana fermion quantum-dot hybrid system を読みましょう。作成すべき回路図と、Joint Measurement の結果によって適用すべきゲートをまとめた表を論文から引用します。

fig2.PNG
table1.PNG

P は Parity Measurement を示すことに注意してください。また、表を見ると条件が複雑なようにも見えますが、Controll ビットに対して適用するゲートは $P_2 = 0$ のときに Z ゲートを適用するだけでいいことがわかります。また、Target ビットは $P_1$ と M の結果が同じ場合に X ゲートを適用すればよさそうですね。

表にもある通り、この論文では Parity Measurement の結果が 0 のときは奇数パリティであると定義していることに注意してください。Q# では Parity Measurement を行ったとき、固有値が 1 (＝ 偶数パリティ) のときに Result が Zero となるので、ちょうど論理が反転します。回答は以下となります。

operation ControlledX_General (qs : Qubit[]) : Unit {
    
    body (...) {
        // アンシラ ビットの用意
        using(q = Qubit[1]) {
            // 論文に従った名称設定
            let Control = qs[0];
            let Target = qs[1];
            let Ancilla = q[0];
            
            // 回路図通りの処理と観測を実施
            H(Ancilla);
            let p1 = MeasureAllZ([Ancilla, Control]);
            
            H(Ancilla);
            H(Target);
            let p2 = MeasureAllZ([Ancilla, Target]);

            H(Ancilla);
            H(Target);
            let result = M(Ancilla);

            // 論文とは p_2 の論理が逆になります
            if(p2 == One) {
                Z(Control);
            }

            // 同様に、論文とは p_1 の論理が逆になります
            if(p1 != result) {
                X(Target);
            }

            ResetAll(q);

        }
    }
    
    adjoint self;
}

最後に

今回は Joint Measurement として様々な観測を学んできました。私自身、2 量子ゲートの作り方の難しさなどはさっぱり理解ができず、興味もないのですが、こうした観測を利用した処理というのも必要になるということがわかる大変有意義な Kata でした。次回は誤り訂正をまとめる予定です。この記事が Q# や Quantum Katas に取り組み方のお役に立てば幸いです。

4
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?