前書き
本記事では、Quantum Katas の Deutsch-Jozsa Algorithm について解説します。Q# や Quantum Katas って何よという方は Quantum Katas で始める量子コンピュータ入門 |0⟩ をご参照ください。
これまでに BasiGates や SuperPositionで培った基礎知識を生かして、今回は具体的な問題解決を行うアルゴリズムがいよいよ登場します。今回の Kata の題材である Deutsch-Jozsa のアルゴリズムは、"量子コンピューター" という名前が入った論文を最初に書いたイギリスの物理学者 Deutsch が、数学者 Jozsa と共同で考案したアルゴリズムで、世界で初めて量子コンピューターの有効性を示したアルゴリズムです。知名度は Shor のアルゴリズムなどと比べられないくらい低いのですが、歴史的にも非常に需要な意味を持つアルゴリズムとなります。
それでは早速進めていきましょう、、、と行きたいのですが、この Kata 全体を通して共通している問題を先に定義しておきましょう。
問題定義
以下の通り、$n$ ビットの入力 $x$ と 1 ビットの入力 $y$ を用意する。
$$ \boldsymbol x \in \{0, 1\}^n$$
$$ y \in \{0, 1\}$$上記入力 $\mathbb x, y$に対し、以下のような変換 $U_f$ を考える。
$$U_f|\boldsymbol x, y⟩ = |\boldsymbol x, y\oplus f(\boldsymbol x)⟩ $$
ただし、$f(\boldsymbol x) \in \{0, 1\}$ である。
入出力となる量子ビットは $n+1$ ビットありますが、重要な $f(x)$ の中身はブラックボックスとなっています。この $f(x)$ を求めることが、Deutsch-Jozsa のアルゴリズムが解決する問題となります。なんの役に立つんだろうと思った方は正解です。今回の Kata で扱う問題は歴史的には重要な意味を持ちますし、内容も比較的理解しやすいため量子コンピューターの威力を体感するにはうってつけなのですが、残念ながら特に現実世界で役に立つものではありません。ちょっとテンションが下がるかもしれませんが、それでは進めていきましょう。
各 Task の解説
Task 1.1. f(x) = 0
問題
入力: $\boldsymbol x \in \{0, 1\}^n$, $y \in \{0, 1\}$. また、$f(x) = 0$
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$ に変換する
解説
$f(x) = 0$ なので、特に何かをする必要はありません。コメントにも書いてありますが、何もしなくても OK です。
Task 1.2. f(x) = 1
問題
入力: $\boldsymbol x \in \{0, 1\}^n$, $y \in \{0, 1\}$. また、$f(x) = 1$
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$ に変換する
解説
次は $f(x) = 1$ の場合です。これも全く難しくないですね。必ず 1 なので、ただ最終ビット $y$ を反転すればよさそうです。
operation Oracle_One (x : Qubit[], y : Qubit) : ()
{
body
{
X(y);
}
}
Task 1.3. f(x) = xₖ (the value of k-th qubit)
問題
入力: $\boldsymbol x = (x_0, x_1,\dots, x_{n-1}) \in \{0, 1\}^n$, $y \in \{0, 1\}$ と整数$k$、ただし $0 \leq k < n$. また、$f(x) = x_k$
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$ に変換する
解説
問題設定は変わりません。$k$ 番目のビットを $y$ に加えればよいので、$\rm CNOT$ ゲートを使えばよさそうですね。
operation Oracle_Kth_Qubit (x : Qubit[], y : Qubit, k : Int) : ()
{
body
{
AssertBoolEqual(0 <= k && k < Length(x), true, "k should be between 0 and N-1, inclusive");
CNOT(x[k], y);
}
}
Task 1.4. f(x) = 1 if x has odd number of 1s, and 0 otherwise
問題
入力: $\boldsymbol x \in \{0, 1\}^n$, $y \in \{0, 1\}$. また、
f(x) =
\begin{cases}
1 &\text { if } x \text{ has odd number of } 1 \\
0 &\text { otherwise}
\end{cases}
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$ に変換する
解説
ちょっと捻りを加えた問題に見えますが、大したことはありません。「奇数個の 1 を持つなら $f(x) = 1$」 なので、要は $f(x) = \sum x_k$ (ただし mod 2) となることが分かります。全部 $\rm CNOT$ で足してやればよさそうですね。回答は以下です。
operation Oracle_OddNumberOfOnes (x : Qubit[], y : Qubit) : ()
{
body
{
// Hint: f(x) can be represented as x_0 ⊕ x_1 ⊕ ... ⊕ x_(N-1)
for(i in 0..Length(x)-1) {
CNOT(x[i], y);
}
}
}
Task 1.5. f(x) = Σᵢ 𝑟ᵢ 𝑥ᵢ modulo 2 for a given bit vector r (scalar product function)
問題
入力: $\boldsymbol x \in \{0, 1\}^n$, $y \in \{0, 1\}$ および $\boldsymbol r \in \{0, 1\}^n$.
また、$f(x) = \sum r_i x_i$
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$ に変換する
解説
この問題は、これまでのタスク (Task 1.2 は除く) の一般化となります。全ての $i$ に対して$r_i = 0$なら $f(x) = 0$ となるため Task 1.1 となりますし、$i = k$ のときのみ $r_k = 1$ となる場合は Task 1.3 ですね。全ての $i$ に対して $r_i = 1$ なら Task 1.4 となります。
先の Task で作ったオペレーションをそのまま流用できるものではありませんが、Task 1.5 をベースに $\boldsymbol r$ に応じて処理を変えればよさそうですね。 回答は以下です。
operation Oracle_ProductFunction (x : Qubit[], y : Qubit, r : Int[]) : ()
{
body
{
// The following line enforces the constraint on the input arrays.
// You don't need to modify it. Feel free to remove it, this won't cause your code to fail.
AssertIntEqual(Length(x), Length(r), "Arrays should have the same length");
for(i in 0..Length(x)-1) {
if(r[i] == 1) {
CNOT(x[i], y);
}
}
// ...
}
}
Task 1.6. f(x) = Σᵢ (𝑟ᵢ 𝑥ᵢ + (1 - 𝑟ᵢ)(1 - 𝑥ᵢ)) modulo 2 for a given bit vector r
問題
入力: $\boldsymbol x \in \{0, 1\}^n$, $y \in \{0, 1\}$ および $\boldsymbol r \in \{0, 1\}^n$. また、$f(x) = \sum r_i x_i + (1-r_i)(1-x_i)$
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$ に変換する
解説
似たような問題が続きますが、今は忍耐の時です。。。先のタスクでは $r_i x_i$ だけだったのが、$(1-r_i)(1-x_i)$ という項が加えられています。この項が 1 となるのは $r_i = 0$ かつ $x_i = 0$ の時だけですね。回答は以下となります。
operation Oracle_ProductWithNegationFunction (x : Qubit[], y : Qubit, r : Int[]) : ()
{
body
{
AssertIntEqual(Length(x), Length(r), "Arrays should have the same length");
for(i in 0..Length(x)-1) {
if(r[i] == 1) {
CNOT(x[i], y);
}
else {
X(x[i]);
CNOT(x[i], y);
X(x[i]);
}
}
// ...
}
}
Task 1.7. f(x) = Σᵢ 𝑥ᵢ + (1 if prefix of x is equal to the given bit vector, and 0 otherwise) modulo 2
問題
入力: $\boldsymbol x \in \{0, 1\}^n$, $y \in \{0, 1\}$ および $\boldsymbol r \in \{0, 1\}^p$ で $1 \le p \le n$. また、
f(x) = \begin{cases}\sum x_i +1&\text{ if prefix of } x \text{ is equal to } p\\ \sum x_i &\text{ otherwise}\end{cases}
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$ に変換する
解説
この問題くらいになるともはや Deutsch-Jozsa とか関係ないんですが、引き続きいろんな $f(x)$ を作ってみようという問題が続きます。$x$ よりも短い長さ $p$ の $r$ が与えられるので、$r$ が $x$ の前半 $p$ ビットと一致していれば 1 加えろという問題です。
ビットが一致しているかどうかはどう判定すればよいでしょうか。これは、$r_i = 0$ となる場合に $x_i$ を反転する処理を行えば、ビットが一致している場合のみ $x[0..p-1]$ がすべて 1 とできそうです。回答は以下となります。
operation Oracle_HammingWithPrefix (x : Qubit[], y : Qubit, prefix : Int[]) : ()
{
body
{
let P = Length(prefix);
AssertBoolEqual(1 <= P && P <= Length(x), true, "P should be between 1 and N, inclusive");
// 先のTask そのまま
for(i in 0..Length(x)-1) {
CNOT(x[i], y);
}
// 比較対象の prefix が 0 となっている場合は x を反転する
// x と prefix が一致している場合はx[0..P-1] = 11...1 となる
for(i in 0..P-1) {
if (prefix[i] == 0) {
X(x[i]);
}
}
(Controlled X)(x[0..P-1],y);
// 処理のために反転した状態をもとに戻す
for(i in 0..P-1) {
if(prefix[i] == 0) {
X(x[i]);
}
}
}
}
Task 1.8*. f(x) = 1 if x has two or three bits (out of three) set to 1, and 0 otherwise (majority function)
問題
入力: $\boldsymbol x \in \{0, 1\}^3$, $y \in \{0, 1\}$. また、$f(x)$ は多数決関数。
f(x) = \begin{cases}\sum x_i +1&\text{ if prefix of } x \text{ is equal to } p\\ \sum x_i &\text{ otherwise}\end{cases}
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$ に変換する
解説
引き続き Deutsch-Jozsa は関係ないのですが、この問題はビット数が 3 に減っています。その状況で $f(x)$ が多数決関数 (3 ビットのうち 2 ビットを占める値が出力される) ので、$y \oplus f(x)$ は 1 が Majority の場合に$y+1$ となります。
どうやって $x$ の多数を判断すればよいでしょうか。もちろん観測を行えば状態の判別ができますが、その場合は量子ビットの状態が壊れてしまうので、この場合は使えません。こういうときは CNOT ゲートですね。今回は以下のアプローチをとりました。
- $x_0$ と $x_1$ が 1 なら $y$ を反転する
- $x_1$ と $x_2$ が 1 なら $y$ を反転する
- $x_2$ と $x_0$ が 1 なら $y$ を反転する
いずれかの 2 ビットが 1 をとる場合は上記のどれかの条件にだけ合致するため、$y$ が 1 度だけ反転されます。一方 3 ビット全てが 1 をとる場合は上記のすべての条件に合致するため、$y$ は 3 度反転することとなり、結果的には要件は満たせます。回答は以下となります。
operation Oracle_MajorityFunction (x : Qubit[], y : Qubit) : ()
{
body
{
AssertBoolEqual(3 == Length(x), true, "x should have exactly 3 qubits");
CCNOT(x[0], x[1], y);
CCNOT(x[1], x[2], y);
CCNOT(x[2], x[0], y);
}
}
Bernstein-Vazirani のアルゴリズム
ようやく退屈な $f(\boldsymbol x)$ との戯れが終わり、続いては Bernstein-Vazirani のアルゴリズムの登場です。まずは問題定義から行いましょう。
問題
$$ \boldsymbol x \in \{0, 1\}^n$$
$$ y \in \{0, 1\}$$上記入力 $\mathbb x, y$に対し、以下のような変換 $U_f$ を行うブラックボックスが与えられると想定する。
$$U_f|\boldsymbol x, y⟩ = |\boldsymbol x, y\oplus f(\boldsymbol x)⟩ $$
$f(\boldsymbol x)$ は以下の特徴を持つ。
$$f(\boldsymbol x) = \sum_i r_i x_i$$
ここで $\boldsymbol r = (r_0, r_1, \dots, r_{n-1}) \in \{0, 1\}^n$ だが、$\boldsymbol r$ は未知である。
ブラックボックス $U_f$ が与えられた際に、未知の $\boldsymbol r$ を求めよ。
この問題設定からも、役に立つ問題じゃないなと思うかもしれませんが、先にも書いたとおり正解です。ただし、この問題は量子コンピューターの威力を体感するのにうってつけなのです。
まずは古典コンピューターでこの問題をどう解くかを考えてみましょう。単純に考えるのであれば、$r_j$ を求めるためには
x_i = \begin{cases} 1 & \text{ if } i = j \\ 0 & \text {otherwise}\end{cases}
という入力を用意すれば、$n$ 回 $f(\boldsymbol x)$ を試行することで $r_i$ が求められそうです。逆に言えば、$n$ 回の試行が必要そうですね。一方量子コンピューターだとどうなるでしょうか。Bernstein-Vazirani のアルゴリズムでは、この問題を大変エレガントに解決することが可能です。正直にいえば、この問題は普通の人が考えて解決することは現実的ではないので、早速解説からはじめます。
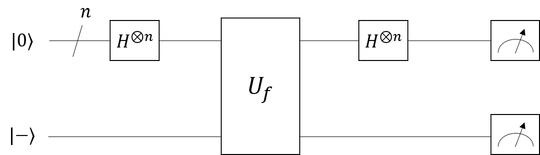
いきなり答えの回路図から始めましょう。答えは以下です。
回路図にもある通り、まずこの問題では入力として利用される $n$ ビットの $\boldsymbol x$ に対してアダマール変換を実施します。一般に、$n$ ビットの量子ビット $|a⟩$ に対するアダマール変換 $H^{\otimes n}$ は以下のように記述されます。(入力として定義した $x$ と区別するために $x'$ を使っています)
H^{\otimes n} |\boldsymbol a⟩ = \frac{1}{\sqrt{2^n}} \sum_{\boldsymbol x' \in \\{0, 1\\}^n} (-1)^{\boldsymbol x'\cdot \boldsymbol a} |\boldsymbol x'⟩
= \frac{1}{\sqrt{2^n}} \sum_{\boldsymbol x' \in \\{0, 1\\}^n} (-1)^{\sum_i a_i x'_i} |\boldsymbol x'⟩
初めて見る方は本当か? と思うかもしれませんが、アダマール変化の定義から $|0⟩$ が $\frac{|0⟩ + |1⟩}{\sqrt 2}$、 $|1⟩$ が $\frac{|0⟩ - |1⟩}{\sqrt 2}$ となることを思い出せば、$|x'⟩$ の係数は $a_i = x_i = 1$ となる $i$ が奇数個ある場合だけ負となることがわかるでしょう。そのため、mod 2 をとれば係数は $(-1)^{\boldsymbol x\cdot \boldsymbol a}$ となることが確かめられます。
今回の問題では入力が $|00\dots 00⟩$ なので
H^{\otimes n} |00\dots00⟩ = \frac{1}{\sqrt{2^n}} \sum_{\boldsymbol x' \in \\{0, 1\\}^n} |\boldsymbol x'⟩
と記述できます。続いて、入力 $y$ として $|-⟩ = \frac{|0⟩ - |1⟩}{\sqrt 2}$ を用意します。$U_f$ の入力として、上記のアダマール後の値と $|-⟩$ を使用すると、$U_f$ 処理後の出力は以下となります。
\begin{align}
U_f(|\boldsymbol x, y⟩)
&= |\boldsymbol x, y\oplus f(\boldsymbol x)⟩ \\
&= \frac{1}{\sqrt{2^n}} \big| \sum_{\boldsymbol x' \in \\{0, 1\\}^n} |\boldsymbol x'⟩, \frac{|0⟩ - |1⟩}{\sqrt 2} \oplus f(\boldsymbol x') \Large⟩ \\
&= \frac{1}{\sqrt{2^{n+1}}} \sum_{\boldsymbol x' \in \\{0, 1\\}^n} \Big( |\boldsymbol x'⟩(|0 \oplus f(\boldsymbol x')⟩ - |1 \oplus f(\boldsymbol x')⟩)\Big)
\end{align}
もうちょっと簡単にならないでしょうか。この問題ではとにかく $f(x)$ の情報が取り出したくて仕方がないので、最後の項に注目してみましょう。すると、
|0 \oplus f(\boldsymbol x)⟩ - |1 \oplus f(\boldsymbol x)⟩ =
\begin{cases}
|0⟩ - |1⟩ &\text{ If } f(\boldsymbol x) = 0 \\
|1⟩ - |0⟩ &\text{ If } f(\boldsymbol x) = 1
\end{cases}
となることがわかります。これをつかうと、上記の項は以下の通りに書き直すことができます。
$$
|0 \oplus f(\boldsymbol x')⟩ - |1 \oplus f(\boldsymbol x')⟩ = (-1)^{f(\boldsymbol x')}\Big(|0⟩ - |1⟩\Big)
$$
これを代入してみましょう。
$$
U_f(|\boldsymbol x, y⟩) = \frac{1}{\sqrt{2^{n+1}}} \sum_{\boldsymbol x' \in \{0, 1\}^n} \Big((-1)^{f(\boldsymbol x')} |\boldsymbol x'⟩(|0⟩ - |1⟩)\Big)
$$
なんということでしょう。 衝撃の展開ですね。この式変形は、$U_f$ の定義から最終ビット $y$ にしか乗らないと思われた未知の$r$ を含む $f(x)$ の情報が、全体の位相に形を変えて現れるということを意味しています。なんということでしょう。ここまで変形すれば、残念ながら $y$ は用なしとなるのです。上位 $n$ ビットだけに注目すると
$$
\frac{1}{\sqrt{2^n}} \sum_{\boldsymbol x' \in \{0, 1\}^n} (-1)^{f(\boldsymbol x')} |\boldsymbol x'⟩
$$
を得ます。さて、ここで今回の問題は
$$f(\boldsymbol x) = \sum_i r_i x_i$$
であったことを思い出しましょう。すると $x'$ は以下のようになります。
\frac{1}{\sqrt{2^n}} \sum_{\boldsymbol x' \in \\{0, 1\\}^n} (-1)^{f(\boldsymbol x')} |\boldsymbol x'⟩
=
\frac{1}{\sqrt{2^n}} \sum_{\boldsymbol x' \in \\{0, 1\\}^n} (-1)^{\sum_i r_i x'_i} |\boldsymbol x'⟩
もうお分かりでしょうか。これはまさしく、アダマール変換の定義そのものです。アダマール変換は 2 回行うと元にもどりますから、上記に再度アダマール変換を施すと、
H^{\otimes n} \Big( \frac{1}{\sqrt{2^n}} \sum_{\boldsymbol x' \in \\{0, 1\\}^n} (-1)^{\sum_i r_i x'_i} |\boldsymbol x'⟩ \Big) = \boldsymbol r
言い換えると、初期状態として $\boldsymbol x = |00\dots 00⟩$ と $y = |-⟩ = \frac{|0⟩ - |1⟩}{\sqrt 2}$ を用意すると、出力される上位 $n$ ビットとして確率 1 で $\boldsymbol r$ が得られるということになります。いやはやなんということでしょう。古典コンピュータでは $n$ 回 $f(x)$ の計算が必要が必要だった $r$ の導出が、たった一回の $U_f$ の計算のみで行えました。なんと美しいことか!!すごいぜ量子コンピューター!!これが役に立つものであればさらに素晴らしいのに!!
というわけで、この先の 2 つの Task は上記をインプリするだけで終了です。
Task 2.1. State preparation for Bernstein-Vazirani algorithm
問題
Bernstein-Vazirani の準備として、$H^{\otimes n}|00\dots00⟩$ と $|-⟩$ を作れ。
解説
省略します!!
operation BV_StatePrep (query : Qubit[], answer : Qubit) : ()
{
body
{
for(i in 0..Length(query)-1) {
H(query[i]);
}
X(answer);
H(answer);
}
adjoint auto;
}
Task 2.2. Bernstein-Vazirani algorithm implementation
問題
Bernstein-Vazirani のアルゴリズムを実装せよ。
解説
実装自体には特に注意点はありません。ここまで Task を進めた方なら、実装は楽勝でしょう。
operation BV_Algorithm (N : Int, Uf : ((Qubit[], Qubit) => ())) : Int[]
{
body
{
// Memo: see also https://arxiv.org/pdf/1609.03185.pdf
mutable r = new Int[N];
using (x = Qubit[N]) {
using (y = Qubit[1]) {
ResetAll(x);
Reset(y[0]);
// n 次アダマール変換実施
for(i in 0..Length(x)-1) {
H(x[i]);
}
// |-⟩ を用意
X(y[0]);
H(y[0]);
Uf(x, y[0]);
// n 次アダマール変換実施
for(i in 0..Length(x)-1) {
H(x[i]);
}
// 観測結果を r に代入
for(i in 0..Length(x)-1) {
if(M(x[i]) == Zero) {
set r[i] = 0;
}
else {
set r[i] = 1;
}
}
ResetAll(x);
Reset(y[0]);
}}
return r;
}
}
Deutsch-Jozsa のアルゴリズム
さて、Bernstein-Vazirani のアルゴリズムで量子コンピューターの威力と美しさに触れることができましたが、続いてはこの Kata のタイトルにもなっている Deutsch-Jozsa のアルゴリズムです。早速問題定義からいきましょう。
問題
$$ \boldsymbol x \in \{0, 1\}^n$$
$$ y \in \{0, 1\}$$上記入力 $\mathbb x, y$に対し、以下のような変換 $U_f$ を行うブラックボックスが与えられると想定する。
$$U_f|\boldsymbol x, y⟩ = |\boldsymbol x, y\oplus f(\boldsymbol x)⟩ $$
ここで、$f(\boldsymbol x)$ は以下の特徴を持つ。
f(\boldsymbol x) = \begin{cases} \text{constant} & (\text{入力に関係なく0、もしくは入力に関係なく 1}) \\ \text{balanced} &(\text{0 と 1 をちょうど半々で返す}) \end{cases}
ブラックボックス $U_f$ が与えられた際に、$f(\boldsymbol x)$ が constant か balanced かを判定せよ。
上記の通り、問題設定は Bernstein-Vazirani のアルゴリズムと大差はありません。まずは古典コンピューターでこの問題をどう解くかを考えてみましょう。ブラックボックスしか与えられないため、$f(\boldsymbol x)$ が constant か balanced かを判定するためには、何度か入力を変えて試してみないとダメそうです。1 番うれしいパターンとしては、$f(\boldsymbol x)$ を 2 回通したら 0 と 1 が出力され、balanced であることが決定できる場合ですね。この場合は、2 回の試行で結論が導出されます。一方、balanced であったとしても最悪の場合は、$\frac{n}{2} +1$ 回の試行が必要となります。さらに、constant である場合は必ず $\frac{n}{2} +1$
回の試行が必要となり、ある意味運任せの探索が必要となることが想定されるでしょう。
こちらも回答からになりますが、利用する回路自体は Bernstein-Vazirani で利用したものと全く同一となります。
さらにいえば、入力の用意も全く同じなのです。そのため、Bernstein-Vazirani と同様に必要となる $f(x)$ の計算回数も 1 回ですし、式変形も以下の $n$ ビットを求めるまでは同じです。
$$
\frac{1}{\sqrt{2^n}} \sum_{\boldsymbol x' \in \{0, 1\}^n} (-1)^{f(\boldsymbol x')} |\boldsymbol x'⟩
$$
Bernstein-Vazirani の場合は $f(\boldsymbol x)$ が内積で書かれていたのでアダマール変換を施すとすぐに $r$ が求められましたが、今回はそこまで簡単にはいきません。さて、どうなるでしょう?計算してみましょう。
\begin{align}
H^{\otimes n}\left(\frac{1}{\sqrt{2^n}} \sum_{\boldsymbol x' \in \\{0, 1\\}^n} (-1)^{f(\boldsymbol x')} |\boldsymbol x'⟩
\right)
&= \frac{1}{2^n} \sum_{\boldsymbol x' \in \\{0, 1\\}^n} \sum_{\boldsymbol z \in \\{0, 1\\}^n} (-1)^{\boldsymbol z\cdot \boldsymbol x' \oplus f(\boldsymbol x')} |\boldsymbol z⟩ \\
&= \frac{1}{2^n} \sum_{\boldsymbol z \in \\{0, 1\\}^n} \sum_{\boldsymbol x' \in \\{0, 1\\}^n} (-1)^{\boldsymbol z\cdot \boldsymbol x' \oplus f(\boldsymbol x')} |\boldsymbol z⟩
\end{align}
なかなかややこしい形をしていますが、上記からは最終的に $\boldsymbol z$ という状態となる確率振幅が
$$\frac{1}{\sqrt{2^n}}\sum_{\boldsymbol x' \in \{0, 1\}^n} (-1)^{\boldsymbol z\cdot \boldsymbol x' \oplus f(\boldsymbol x')}$$
と記述されることがわかります。さて、それでは $\boldsymbol z = |00\dots 00⟩$ となる確率振幅はどうなるでしょうか。代入して計算してみましょう。
\frac{1}{\sqrt{2^n}}\sum_{\boldsymbol x' \in \\{0, 1\\}^n} (-1)^{\boldsymbol z\cdot \boldsymbol x' \oplus f(\boldsymbol x')} =
\sum_{\boldsymbol x' \in \\{0, 1\\}^n} (-1)^{f(\boldsymbol x')}=
\begin{cases}
1 &\text{ If } f(\boldsymbol x') = 0 \\
-1 &\text{ If } f(\boldsymbol x') = 1 \\
0 &\text{otherwise}
\end{cases}
おわかりでしょうか。上記を言い換えると、$f(\boldsymbol x')$ が Constant なら確率 1 で$|00\dots 00⟩$ が観測される( $|00\dots 00⟩$ しか観測されない)し、逆に Balanced なら $|00\dots 00⟩$ は観測されない、ということを言っています。Bernstein-Vazirani では $r$ がそのまま得られましたが、今回は出力が $|00\dots 00⟩$ となるかどうかで問題に解答することができます。これもなんとすごい!!
Task 3.1. Deutsch-Jozsa algorithm implementation
問題
Deutsch-Jozsa のアルゴリズムを実装し、$f(x)$ が Constant か Balanced かを判別せよ。
回答
これも実装自体は楽勝ですね。
operation DJ_Algorithm (N : Int, Uf : ((Qubit[], Qubit) => ())) : Bool
{
body
{
mutable isConstantFunction = true;
using (x = Qubit[N]) {
using (y = Qubit[1]) {
ResetAll(x);
Reset(y[0]);
// n 次アダマール変換実施
for(i in 0..Length(x)-1) {
H(x[i]);
}
// |-⟩ の用意
X(y[0]);
H(y[0]);
Uf(x, y[0]);
// n 次アダマール変換実施
for(i in 0..Length(x)-1) {
H(x[i]);
}
let first = M(x[0]);
for(i in 0..Length(x)-1) {
if(M(x[i]) != Zero) {
set isConstantFunction = false;
}
}
ResetAll(x);
Reset(y[0]);
}}
return isConstantFunction;
}
}
Task 4.1. Reconstruct the oracle from task 1.6
問題
$$ \boldsymbol x \in \{0, 1\}^n$$
$$ y \in \{0, 1\}$$上記入力 $\mathbb x, y$に対し、以下のような変換 $U_f$ を行うブラックボックスが与えられると想定する。
$$U_f|\boldsymbol x, y⟩ = |\boldsymbol x, y\oplus f(\boldsymbol x)⟩ $$
ここで、$f(x) = \sum r_i x_i + (1-r_i)(1-x_i)$。
ブラックボックス $U_f$ が与えられた際に、$f(\boldsymbol x)$ と同じ結果を得ることができる $r$ を求めよ。
解説
正直に言えば、Kata 全体の中で一番腹が立った問題がこの問題です。Bernstein-Vazirani、Deutsch-Jozsa と大変美しいエレガントな問題が続いた後では蛇足といってもいいでしょう。問題文の原文は出力として A bit vector r which generates the same oracle as the one you are given を行えとのことなのですが、最初はニュアンスを見落としていました。全く同じ $r_i$ を復元することは要求されていません。
まず、そもそもこの問題ではアダマール変換は出てきませんし、なんなら入力 $\boldsymbol x$、$y$ は意味を持ちません。初期状態は $x = |00\dots 00⟩$ なので、$f(x)$ は
\begin{align}
f(\boldsymbol x) &= \sum_k{r_kx_k + (1-r_k)(1-x_k)} \\
&= 2\sum r_kx_k - \sum r_k - \sum x_k + n \\
&= \sum r_k + n
\end{align}
となります。上記から
\begin{align}
U_f(|x, y⟩)
&= |00\dots 00, f(x)⟩ \\
&= |00\dots 00, \sum r_k + N⟩
\end{align}
であることがわかります。$n$ が奇数なら $+1$ なので、最終ビットをFlip すると
U_f(|x, y⟩) = |00\dots 00, \sum r_k⟩
となります。要は、$r_k$ の合計数が $1$ か $0$ かだけの情報が最終ビットに乗っていて、観測することで取得が可能。
言い換えると、このビットだけ $\boldsymbol r$ の任意の箇所に設定すれば、$\sum r_k$ の値は同じにできます。なんじゃそりゃ。。。
operation Noname_Algorithm_Reference (N : Int, Uf : ((Qubit[], Qubit) => ())) : Int[]
{
body
{
mutable r = new Int[N];
using (qs = Qubit[N+1]) {
let x = qs[0..N-1];
let y = qs[N];
Uf(x, y);
// 奇数なら最終ビットを Flip
if (N % 2 == 1) {
X(y);
}
let m = M(y);
// 最終ビットが |1⟩ なら r のどこかを 1 に
if (m == One) {
set r[0] = 1;
}
ResetAll(qs);
}
return r;
}
}
最後に
これで Deutsch-Jozsa のアルゴリズムは終了です。最後の Task でいい気分が台無しなのですが、ようやく量子コンピューターがうまく計算できる例が見えましたね。
次は決めていませんが、Superdence Coding あたりでお会いしましょう。