前書き
本記事は量子コンピュータ Advent Calendar 2018 - Qiita の 12/4 分です。
タイトルにもある Quantum Katas というのは Q# を開発している Microsoft 自身が提供している Q# の問題集群となります。2018 年 12 月現在では 10 個の Kata が提供されています。これまでに各 Kata の解説を 5 つほどまとめてきたので、今回は第 $|6⟩$ 弾としてサイモンのアルゴリズムの Q# 実装を解説したいと思います。Q# や Quantum Katas って何よという方は Quantum Katas で始める量子コンピュータ入門 |0⟩ をご参照ください。
サイモンの問題
まずは問題の定義から始めましょう。今回の Kata で取り扱うサイモンの問題とは以下のような問題のことを言います。
サイモンの問題
以下のような関数 $f$
$$f: \{0, 1\}^n \rightarrow \{0, 1\}^n$$
が正の整数 $n$ を使って記述されるとする。この $f$ は周期 $s\in \{0,1\}^n$を持つと仮定する。すなわち
$$f(x) = f(y) \text{ if and only if } x\oplus y \in \{0^n, s\}$$
上記のような $f$ を実行するブラックボックス $U_f$ が与えられたとき、$f$ が持つ周期 $s$ を求めよ。
ただし、$U_f$ は以下のように与えられる。
$$U_f|x⟩|y⟩ = |x⟩|y ⊕ f(x)⟩$$
なんか難しいことを言っているような気もしますが、要は周期を求めなさいという問題になります。$f$ の定義自体が与えられるわけではないので、何回も実行して入出力くらべなきゃだめそうだなーというのが最初の印象でしょうか。実際、この問題は古典コンピューターでは多項式時間では解くことができません。
各 Task の解説
最終目標は上記のサイモンの問題を解くためのサイモンのアルゴリズムを実装することなのですが、Quantum Katas ではアルゴリズム実装に至るまでの下準備も含める形で問題が構成されています。順にみていきましょう。
Task 1.1. f(x) = 𝑥₀ ⊕ ... ⊕ xₙ₋₁ (i.e., the parity of a given bit string)
問題
入力: 長さ $N$ の量子ビット $|x⟩$ と長さ 1 の量子ビット$|y⟩$
ゴール: $|x, y⟩$ を $|x, y ⊕ x_0 ⊕ x_1 ... ⊕ x_{n-1}⟩$ に変換する。
解説
サイモンの問題では $N$ 量子ビットを扱うのですが、まずは練習として $y$ が長さ 1 の場合を考えます。また、$f$ に相当する変換も周期性を持つような内容ではなく、直接的にはサイモンの問題とは関係ありません。あくまで Q# の練習とお考え下さい。しばらくは Q# での量子ビットとの戯れが続きます。
指定された処理であれば CNOT ゲートをすべての $x_i$ を利用して処理してあげればよさそうですね。回答は以下となります。
operation Oracle_CountBits (x : Qubit[], y : Qubit) : ()
{
body
{
for(i in 0..Length(x)-1) {
CNOT(x[i], y);
}
}
adjoint auto;
}
Task 1.2. Bitwise right shift
問題
入力: 長さ $N$ の量子ビット $|x⟩$ と長さ $N$ の量子ビット$|y⟩$
ゴール: $|x, y⟩$ を $|y_0, y_1 ⊕ x_0, y_2 ⊕ x_1, ..., y_{n-1} ⊕ x_{n-2}⟩$ に変換する。
解説
これも引き続き Q# の練習です。先ほどと同様に、CNOT ゲートを利用すればよさそうですね。
operation Oracle_BitwiseRightShift (x : Qubit[], y : Qubit[]) : ()
{
body
{
for(i in 0..Length(x)-2) {
CNOT(x[i], y[i+1]);
}
}
adjoint auto;
}
Task 1.3. Linear operator
問題
入力: 長さ $N$ の量子ビット $|x⟩$ と長さ $1$ の量子ビット$|y⟩$、サイズ $1 \times N$ のバイナリ値を持つ行例 $A$
ゴール: : $|x, y⟩$ を $|y ⊕ Ax⟩$ に変換する。
解説
これも引き続き Q# の練習です。問題上は $A$ は (0, 1 の 2 値しかもたないのに) Int として与えられているところは少しご注意ください。
operation Oracle_OperatorOutput (x : Qubit[], y : Qubit, A : Int[]) : ()
{
body
{
for(i in 0..Length(x)-1) {
if(A[i] == 1) {
CNOT(x[i], y);
}
}
}
adjoint auto;
}
Task 1.4. Multidimensional linear operator
問題
入力: 長さ $N_1$ の量子ビット $|x⟩$ と長さ $N_2$ の量子ビット$|y⟩$、サイズ $N_2 \times N_1$ のバイナリ値を持つ行例 $A$
ゴール: $|x, y⟩$ を $|y ⊕ Ax⟩$ に変換する。
解説
これも同じ問題ですね。まだサイモンの問題とは直接関係ありません。先にも書いた通り、しばらくは Q# との戯れが続きます。あんまりおもしろくはないですね。
operation Oracle_MultidimensionalOperatorOutput (x : Qubit[], y : Qubit[], A : Int[][]) : ()
{
body
{
for(i in 0..Length(x)-1) {
for(j in 0..Length(y)-1) {
if(A[j][i] == 1) {
CNOT(x[i], y[j]);
}
}
}
}
adjoint auto;
}
Task 2.1. State preparation for Simon's algorithm
問題
入力: 長さ $N$ の量子ビット $: $|00\dots00⟩$
ゴール: すべての状態が等しい確率で重ねあわされた状態 $\frac{|00\dots00⟩ +|00\dots01⟩ + \cdots + |11\dots10⟩ +|11\dots11⟩}{\sqrt 2^N}$ に変換する。
解説
この問題で少し毛色が変わりました。タイトルの通り、サイモンのアルゴリズムに向けた準備です。
しかしこの問題も難しくはありません。ドイチェ・ジョザでもバーンスタイン・ヴァジラニでも実施するように、全量子ビットをアダマール変換すれば終わりです。回答は以下となります。
operation SA_StatePrep (query : Qubit[]) : ()
{
body
{
for(i in 0..Length(query)-1) {
H(query[i]);
}
}
adjoint auto;
}
サイモンのアルゴリズムについて
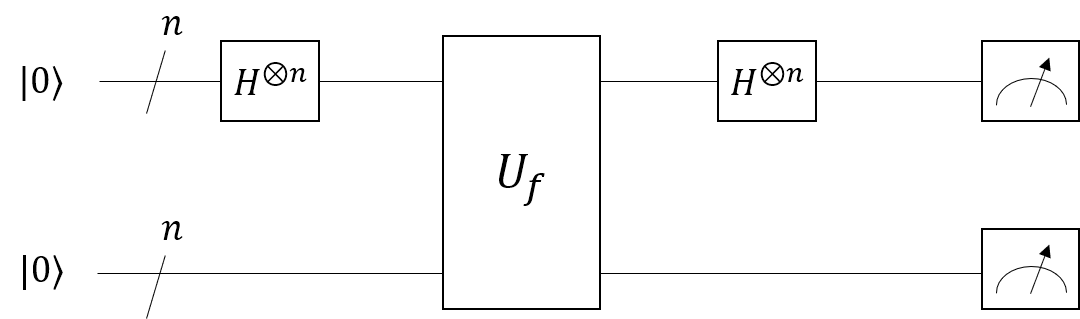
さあ!! 長く Q# との戯れが続きましたが、ようやくこの記事の冒頭で記載したサイモンの問題を量子コンピューターを使って解く、サイモンのアルゴリズムの登場です。早速回答からになりますが、今回 Q# で実装する回路図を先にお見せしましょう。
まあこの時点ではふーんくらいかもしれません。なんでこの回路でサイモンの問題が解けるのか、すなわち隠された関数 $f$ に秘められた周期が見つけ出せるのか、解説していきます。見やすさのために、問題を再掲しますね。
サイモンの問題(再掲)
以下のような関数 $f$
$$f: \{0, 1\}^n \rightarrow \{0, 1\}^n$$
が正の整数 $n$ を使って記述されるとする。この $f$ は周期 $s\in \{0,1\}^n$を持つと仮定する。すなわち
$$f(x) = f(y) \text{ if and only if } x\oplus y \in \{0^n, s\}$$
上記のような $f$ を実行するブラックボックス $U_f$ が与えられたとき、$f$ が持つ周期 $s$ を求めよ。
ただし、$U_f$ は以下のように与えられる。
$$U_f|x⟩|y⟩ = |x⟩|y ⊕ f(x)⟩$$
解説
早速回路図通りに計算を進めます。まずは 2 つの $N$ ビットの入力のうち片方にすべてアダマール変換を実施します。
$$
H^{\otimes n} |00\dots00⟩ = \frac{1}{\sqrt{2^n}} \sum_{x_a \in \{0, 1\}^n} |x_a⟩
$$
上記のアダマール済みの量子ビットと、初期状態の量子ビット $|y⟩$ を $U_f$ に入力しましょう。
\begin{align}
U_f(H^{\otimes n} |00\dots00⟩)|y⟩ &= \frac{1}{\sqrt{2^n}} \sum_{x_a \in \\{0, 1\\}^n} |x_a⟩(|00\dots00⟩\oplus |f(x_a)⟩) \\
&= \frac{1}{\sqrt{2^n}} \sum_{x_a \in \\{0, 1\\}^n} |x_a⟩|f(x_a)⟩ \\
\end{align}
思ったよりすっきりした形になりましたね。回路図によると、再度上位 $N$ ビットをアダマール変換するようです。
$N$ ビットの任意の量子ビット $|a⟩$ のアダマール変換は
$$
H^{\otimes n} |a⟩ = \frac{1}{\sqrt{2^n}} \sum_{ x \in \{0, 1\}^n} (-1)^{x\cdot a} |x⟩
$$
と書けることに注意しましょう。さあ、ちょっと式は複雑っぽい感じになりますが、アダマール変換後は以下のようになります。
\begin{align}
H^{\otimes n} (U_f)
&=\frac{1}{\sqrt{2^n}} \sum_{x_a \in \\{0, 1\\}^n} \frac{1}{\sqrt{2^n}} \sum_{y_a \in \\{0, 1\\}^n} (-1)^{y_a\cdot x_a} |y_a⟩|f(x_a)⟩\\
&=\frac{1}{2^n} \sum_{x_a \in \\{0, 1\\}^n} \sum_{y_a \in \\{0, 1\\}^n} (-1)^{y_a\cdot x_a} |y_a⟩|f(x_a)⟩ \\
&=\frac{1}{2^n} \sum_{y_a \in \\{0, 1\\}^n} |y_a⟩ \sum_{x_a \in \\{0, 1\\}^n} (-1)^{y_a\cdot x_a} |f(x_a)⟩
\end{align}
さて、何がしたかったんでしたっけ?今回は、$f$ に隠された周期 $s$ を求めたいのでした。え、$s$ どこ?
…さあ、ここから先は場合分けをして考えていきます。まずは最初に $s = 0$ を考えましょう。この時、$f$ は全単射になることがわかります。$f$ の定義から全射であることは自明ですが、$f(x_1) = f(x_2)$ の場合 $x_1 = x_2$ となるため、この場合は単射となることもわかりますね。要は 1 対 1 で対応する、ということを難しくいっているだけです。じゃあ、$f$ が全単射の場合はどうなるでしょう?
場合1:f が全単射の場合
まずは、$f$ が全単射の場合、上位 $N$ 量子ビットの状態 $|y_a⟩$ が観測される確率を考えると、その確率は
$$
\left| \frac{1}{2^n} \sum_{x_a \in \{0, 1\}^n} (-1)^{y_a\cdot x_a} |f(x_a)⟩ \right|^2
$$
となります。$f(x)$ は全単射なので、$\sum f(x_a) = \sum x_a$ が成り立ちます。そのため、上記の難し気な式はちょっと簡単化できそうです。また、そうなると係数が消しあうこともなさそうなので、2 乗をとれば 1 になる、すなわち無視してしまってもよさそうです。というわけで、係数は
$$
\left| \frac{1}{2^n} \sum_{x_a \in \{0, 1\}^n} (-1)^{y_a\cdot x_a} |f(x_a)⟩ \right|^2 = \left| \frac{1}{2^n} \sum_{x_a \in \{0, 1\}^n} |x_a⟩ \right|^2 = \frac{1}{2^n}
$$
となることがわかります。なんかややこしい気もしますが、要は $f$ が全単射なら、上位 $N$ 量子ビットを観測したときの確立はすべての量子ビットの重ね合わせが等しく観測される (アダマール変換しただけの状態と同じともいえる) ということを示しています。
もう数式でおなか一杯感もありますが、続きます。
場合2: f が全単射ではない場合
続いて $f$ が全単射ではない場合、言い換えると $f(x_1) = f(x_2)$ で $x_1 = x_2 \oplus s$ を満たす $s \not = 0$ が存在する場合を考えます。先ほどと同様に上位 $N$ 量子ビットの状態 $|y_a⟩$ が観測される確率を考えましょう。ここで、$f(x_a)$ の値域を $A = \rm{Range} (f)$ と置くと、
$$
\left| \frac{1}{2^n} \sum_{x_a \in \{0, 1\}^n} (-1)^{y_a\cdot x_a} |f(x_a)⟩ \right|^2 = \left| \frac{1}{2^n} \sum_{x_b \in A} (-1)^{y_a\cdot x_b} |f(x_b)⟩ \right|^2
$$
とかけることがわかります。このとき、問題の定義から$f(x_{1b}) = f(x_{2b})$, $x_1 = x_2 \oplus s$ となる組み合わせが存在するので、さらにゴリゴリ変形していくと
\begin{align}
\left\|
\frac{1}{2^n} \sum_{x_b \in A} \Large(
(-1)^{y_a\cdot x_{1b}} +
(-1)^{y_a\cdot x_{2b}}
\Large)|f(x_b)⟩
\right\|^2
&=
\left\|
\frac{1}{2^n} \sum_{x_b \in A} \Large(
(-1)^{y_a\cdot (x_2b \oplus s)} +
(-1)^{y_a\cdot x_{2b}}
\Large)|f(x_b)⟩
\right\|^2 \\
&=
\left\|
\frac{1}{2^n} \sum_{x_b \in A} \Large(
(-1)^{(y_a\cdot x_2b) \oplus (y_a \cdot s)} +
(-1)^{y_a\cdot x_{2b}}
\Large)|f(x_b)⟩
\right\|^2 \\
&=
\left\|
\frac{1}{2^n} \sum_{x_b \in A} (-1)^{y_a\cdot x_{2b}} \Large(
(-1)^{y_a \cdot s} +
1
\Large)|f(x_b)⟩
\right\|^2 \\
\end{align}
が得られます。ようやく求めたかった $s$ の野郎をあぶりだすことに成功しました。上記は何をいっているのでしょう?
上記の式からは、ある $|y_a⟩$ が観測される確率は $(-1)^{y_a \cdot s} + 1$ が含まれるため、
- $s \cdot y_a = 1$ なら 0 になるし、
- $s \cdot y_a = 0$ なら各 $x_b$ ごとに $\frac{2}{2^n} = \frac{1}{2^{n-1}}$ となる、すなわちその他の状態が等確率で重ねあわされている
ということを示しています。え、だから? という声も聞こえそうですが、まとめるとこういうことになります。
- 関数 $f$ が周期 $s$ を持つとき、アダマール変換 → $U_f$ → アダマール変換という処理をすると、上位ビット $y_a$ は $y_a \cdot s = 0$ を満たす $y_a$ が等確率で観測される。
- 何度か上記の処理を行えば、様々な $y_a \cdot s = 0$ を満たす $y_a$が得られるため、$s$ が導出できる。
何度かとかかいて濁していますが、じゃあ何回くらいやれば $s$ を推察することができるんでしょう。
いろんな $y_a$ が観測できれば、
\begin{align}
y_1\cdot s &= 0 \\
y_2\cdot s &= 0 \\
\vdots \\
y_{n-2}\cdot s &= 0 \\
y_{n-1}\cdot s &= 0 \\
\end{align}
という $y_1, y_2,\dots,y_{n-1}$ が得られます。これが線形独立ならば方程式として解くことができそうです。(これは Mod 2 の世界であることにちょっと注意が必要ですが)
本当にこんな $y$ って得られますかね? 直感的にも、$2^{N-1}$ 通りの $y_a$ の中から独立な $N-1$ 個の $y_a$ を求めるというのはそれなりの確率で実現できそうな気がしますが、どのくらいの確率で得られるか確かめてみましょう。しょっぱなの観測で得られた $y_1$ は何の問題もありません。2 回目の観測で得られた $y_2$ が $y_1$ と線形独立である確率は、
$$
1- \frac{1}{2^{N-1}}
$$
ですね。続いて $y_3$ を観測したときに $y_3$ が $y_1$ とも $y_2$ とも独立である確率は、
$$
1- \frac{2}{2^{N-1}}
$$
となります。一般に、$y_1, y_2,\dots,y_{k}$ が線形独立であるときに、$y_{k+1}$ が線形独立である確率は $\frac{2^{n-1} - 2^k}{2^{n-1}}$ と記述されます。そのため、 $n-1$ 個の方程式が線形独立である確率は
$$
(1-\frac{1}{2^{N-1}})(1-\frac{1}{2^{N-2}})\cdots(1-\frac{1}{4})(1-\frac{1}{2})
$$
となります。どのくらいの値になるかの下限を知るために $N \rightarrow \infty$ とすると、だいたい 0.29 くらいの値に収束します。すなわち、どれだけ悪くとも 3 割くらいの確率で線形独立な $n-1$ 個の方程式が得られることがわかります。この方程式から $s$ を求めれば、問題は終了です。
さあ、長々と書いてきましたが、要は Q# で実装しなければならない部分は先に記載した回路図だけです。
operation Simon_Algorithm (N : Int, Uf : ((Qubit[], Qubit[]) => ())) : Int[]
{
body
{
// 観測結果用
mutable b = new Int[N];
using(x = Qubit[N]) {
using(y = Qubit[N]) {
// アダマール変換(Task2.1 を使っています)
SA_StatePrep(x);
Uf(x,y);
// アダマール変換
SA_StatePrep(x);
// 観測結果を代入
for(i in 0..N-1) {
if(BoolFromResult(M(x[i]))) {set b[i] = 1;}
else {set b[i] = 0;}
}
ResetAll(x);
ResetAll(y);
}}
return b;
}
}
あれ?頑張って計算した、$n-1$ 回繰り返して $s$ を求めるところはどこへ行ったのでしょう??
実はこの Kata では、量子計算のいらない $s$ 自身の導出 (これを Classical post-processing とかいうそうです) は C# のコードで実装済みなので、Kata を進める上では実装の必要はないのです。なんじゃそりゃ。
まとめ
この記事では Quantum Katas の Simon's Algorithm を解説しました。周期を求めるという意味が直接的に感じにくい内容でしたが、これがかの有名な Shor のアルゴリズムにつながっていくのです。また、$|4⟩$ で解説したドイチェ・ジョザは、確率 1 で正しい回答が得られる決定的アルゴリズムでしたが、今回のサイモンは確率的アルゴリズムになっています。また、post-porcessing が必要となるという所も大きな違いでした。
この記事が少しでもサイモンのアルゴリズムや Q# の勉強をされる方のお役に立てば幸いです。アドベント カレンダー以外の時期にも、引き続き残りの Kata の解説を続けていくつもりですので、興味のある方はぜひ一緒にやりましょう。