[Python]二分探索(bisect) ABC143D

当内容は、他サイトを参考に自分用に編集したものです。

二分探索の動機

ソートされたリストに対してソート順序を保ったまま値を挿入したいと思う場面は少なくないはずです。そういった場面に 出くわしたときにappendしてsortしているとパフォーマンスはよくないです。Pythonのlistのソートの平均時間計算量は$O(n \log{n})$です。要素数が増えてきたり、毎度ソートしていたりすると実行速度にも影響がでてくると思います。

A = [1, 12, 23, 38, 54, 66, 76, 98]
# Aの順序を保ったまま'46'を挿入したい
A.append(46)
A.sort()
print(A)
# [1, 12, 23, 38, 46, 54, 66, 76, 98]

今回は、上記の方法よりも効率よく、ソートされたリストに対してソート順序を保ったまま値を挿入する二分探索法のPython標準ライブラリ「bisect」(bisection)について説明します。

bisectとは

「bisect」は「二分探索」を利用することで効率よく、リストをソートされた状態に保つことをサポートするためのPython標準ライブラリです。二分探索(binary search)はソート済みの配列に対する探索アルゴリズムです。知っている人は多いと思うのでアルゴリズム自体の詳細は割愛しますが、このアルゴリズムでの時間計算量は$O(\log{n})$です。上記のソートと比べるてパフォーマンスが向上する理由は、リストの順序を保つための計算量が少なくて済むからです。

bisectはPython標準ライブラリなのでなにもインストールせずにimportするだけで使えます。

import bisect

使い方

実際にbisectの使い方について説明します。bisectには挿入箇所を探索する関数(bisect)と探索と挿入を同時に行う(insort)の主に２つの関数が存在しています。

bisect系は以下の３つの関数が存在しています。

• bisect_left
• bisect_right
• bisect

insort系は以下の３つの関数が存在しています。

• insort_left
• insort_right
• insort

それぞれの関数について説明します。

bisect_left

bisect.bisect_left(a, x, lo=0, h=len(a))

引数は以下になります(他の関数においても同様)
a: ソート済みリスト
x: 挿入したい値
lo: 探索範囲の下限
hi: 探索範囲の上限
(lo, hiはスライスと同様の指定方法)

bisect_leftはソートされたリストaに対して順序を保ったままxを挿入できる箇所を探索します。leftが示す通り、aにすでにxが存在している場合は、挿入箇所は既存のxよりも左側になります。また、lo, hiを指定することで探索範囲を絞り込むことも可能です。デフォルトはaの全体が探索対象です。

A = [1, 2, 3, 3, 3, 4, 4, 6, 6, 6, 6]
print(A)
index = bisect.bisect_left(A, 3) # 2 最も左(前)の挿入箇所が返ってきている
A.insert(index, 3)
print(A) # [1, 2, 3, 3, 3, 3, 4, 4, 6, 6, 6, 6]

# 探索範囲を絞り込む
A = [1, 2, 3, 3, 3, 0, 0, 0, 0, 0, 0]
index = bisect.bisect_left(A, 3, 0, 5)
print(index)# 2

bisect_right

名前からも見当がつくように、bisect_leftのxの挿入箇所が既存のxより右になったものです。

A = [1, 2, 3, 3, 3, 4, 4, 6, 6, 6, 6]
print(A)
index = bisect.bisect_right(A, 3) # 5

bisect

こいつはbisect_rightのaliasなので、明示的に書くという意味では使用場面はないかもしれません。

insort_left

insort_left(a, x)はa.insert(bisect.bisect_left(a, x))と同じです。つまり、探索を行い、挿入までを行います。

A = [1, 2, 3, 3, 3, 4, 4, 6, 6, 6, 6]
bisect.insort(A, 3) # [1, 2, 3, 3, 3, 3, 4, 4, 6, 6, 6, 6]

insort_right

insort_right(a, x)はa.insert(bisect.bisect_right(a, x))と同じです。

insort

こいつもinsort_rightのaliasです...

ABC143D

まずナイーブには ${}_N C _3$ 通りの選び方を全(線形)探索する方法が考えられる。しかし $O(N^{3})$ かかって間に合わない (上手く枝刈りすると間に合ってしまったらしいが...)
そこで、こういうときによく考えるのが

• 3 つのうち、2 つを固定して考える

というあたり。とりあえず三角形の三辺を短い順に a,b,c (a≤b≤c) として、

a,b を固定
b,c を固定

といったあたりが思いつく。どちらでやっても解ける。ここでは a,b を固定してやってみる。

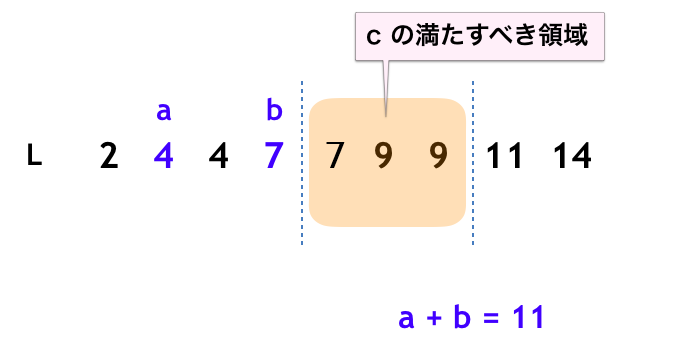
L のうちの a,b を固定すると、残りの辺 c の満たすべき条件は

• c<a+b

となる。下図のような感じ。a=4,b=7 のとき、a+b=11 なので、c のとりうる範囲は、下図のように

• b より右側
• 11 未満の領域

ということになる。

ここで、L のうち「最初に a+b 以上になってしまうインデックス」は二分探索で求めることができる。bisect_left を使う。

まとめると

• a,b を全探索
• L の中で最初に a+b 以上になってしまうインデックスを求める
• c の動ける範囲がそれによって求まるので、合計していく

という風に解ける。a,b の固定方法が $O(N^{3})$ だけあって、それに応じて c の動ける範囲を求めるのは二分探索で $O(\log{N})$ でできるので、全体の計算量は $O(N^{2} \log{N})$ となる。

ABC143D.py

import bisect

n = int(input())
bar_list = list(map(int,input().split()))

#bisectを使うために、リストをソートする
bar_list.sort()

cnt = 0

#aを固定
for i in range(n):
    #bを固定
    for j in range(i+1,n):
        #最初に a+b 以上になってしまうインデックスを二分探索(bisect)
        x = bisect.bisect_left(bar_list,bar_list[i]+bar_list[j])

        #c の満たすべき領域にある棒を数える
        cnt += x-j-1

print(cnt)

　
bisectの内容は、次を参考にした。
Python標準ライブラリ：順序維持のbisect
ABC143Dの内容は、次を参考にした。
AtCoder ABC 143 D - Triangles (茶色, 400 点)