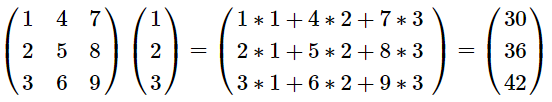はじめに

WebGLはブラウザでGPUを使って3D表示をするためのAPIです。
WebGL 2.0は1.0に比べてGPUによる汎用計算(GPGPU)の機能が強化されています。

WebGLは複雑な手順に従ってAPIを呼ぶ必要があり使いづらいので、簡単にGPGPUのプログラムを作れるライブラリを作ってみました。

以下ではこのライブラリの使い方を説明します。

ライブラリの詳しい説明は以下にあります。
http://lkzf.info/gpgpu.js/doc/

ソースはGitHubに上げています。

https://github.com/teatime77/gpgpu.js/blob/master/js/gpgpu.js

ライブラリの本体はgpgpu.jsという1個のファイルです。
このファイルをGitHubからコピーしてきて、HTMLファイルのhead部分に以下の1行を入れてください。

<script type="text/javascript" src="gpgpu.js"></script>

WebGL 2.0は ChromeとFirefox でサポートされていて、WindowsやMacのほか一部のAndroid端末でも動作します。

手持ちの機器でWebGL 2.0が動作するかは以下のページで確認できます。
http://webglreport.com/?v=2

WebGL 2.0でのGPGPUのしくみ

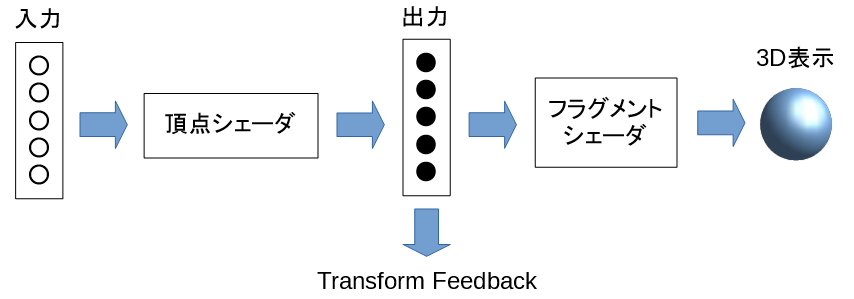
以下はWebGLの通常の3D表示の処理の流れです。
1. 3Dオブジェクトの頂点の位置、色などを頂点シェーダと呼ばれるプログラムに入力します。
2. 頂点シェーダは座標変換などの計算をして出力します。
3. 頂点シェーダの出力はフラグメントシェーダと呼ばれるプログラムに渡されます。
4. フラグメントシェーダは画面の画素ごとの色を計算して3D表示をします。

WebGLでは2.0からTransform Feedbackという機能が追加され、頂点シェーダの出力をアプリ側で受け取れるようになりました。

頂点シェーダの入力,計算,出力はアプリで自由に制御できるので、この仕組みを使ってGPUに数値計算をさせて結果を受け取れます。

ちなみにGPGPUをする場合は、フラグメントシェーダの出力を無効にするようWebGLに指示するので画面には何も表示されません。
フラグメントシェーダの出力を有効にして計算結果を3D表示することも可能です。

頂点シェーダの詳しい書き方はここでは説明していませんが、ウェブには良い記事がたくさんありますのでそちらを参考にしてみてください。

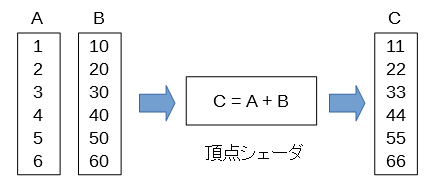
配列の加算

最初に以下のような配列の加算をGPUでしてみます。

以下はプログラムの流れです。

頂点シェーダのプログラムを文字列で記述します。
1. 入力(in)と出力(out)の変数を宣言します。
2. main関数で計算式を書きます。
入力と出力の変数の値をFloat32Arrayの配列で定義します。
GPGPUのオブジェクトを作ります。
計算のパラメータを作ります。
パラメータを使い計算します。
GPGPUのオブジェクトをクリアします。

以下はコードです。

    // 頂点シェーダのプログラムは文字列で記述します。
    var vertex_shader =
       `// 入力変数A
        in  float A;

        // 入力変数B
        in  float B;

        // 出力変数C
        out float C;

        // 要素ごとに呼ばれる関数。
        void main(void ) {
            C = A + B;
    }`;


    // 入力変数AをFloat32Arrayの配列で作ります。
    var A = new Float32Array([ 10, 20, 30, 40, 50, 60 ]);

    // 同様に入力変数Bを作ります。
    var B = new Float32Array([1, 2, 3, 4, 5, 6]);

    // 出力変数Cは配列のサイズ(6)を指定して作ります。
    var C = new Float32Array(6);

    // GPGPUのオブジェクトを作ります。
    var gpgpu = CreateGPGPU();

    // 計算のパラメータを作ります。
    var param = {
        // idはプログラム内でユニークであれば何でも構いません。
        id: "AddVec",

        // 頂点シェーダの文字列を指定します。
        vertexShader: vertex_shader,

        // 頂点シェーダ内の入力と出力の変数名に値を割り当てます。
        args: {
            "A": A,
            "B": B,
            "C": C,
        }
    };

    // パラメータを使い計算します。
    gpgpu.compute(param);

    // GPGPUのオブジェクトをクリアします。
    gpgpu.clear(param.id);

    // 計算結果を表示します。
    document.body.insertAdjacentHTML("beforeend", "<p>A = " + A.join(' ') + "</p>");
    document.body.insertAdjacentHTML("beforeend", "<p>B = " + B.join(' ') + "</p>");
    document.body.insertAdjacentHTML("beforeend", "<p>C = A + B = " + C.join(' ') + "</p>");

サンプルのURL
http://lkzf.info/gpgpu.js/samples/AddVec.html

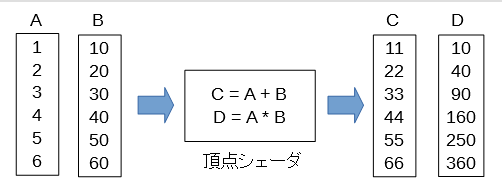
配列の加算と乗算

今度は加算と乗算の2つの値を出力してみます。

頂点シェーダのコード

    // 入力変数A
    in  float A;

    // 入力変数B
    in  float B;

    // 出力変数C
    out float C;

    // 出力変数D
    out float D;

    // 要素ごとに呼ばれる関数。
    void main(void ) {
        C = A + B;
        D = A * B;
    }

1つ注意すべき点は、入力変数と出力変数の要素の数はすべて同じというきまりがあることです。
この例ではA,B,C,Dの各配列の要素数はすべて6になっています。

サンプルのURL
http://lkzf.info/gpgpu.js/samples/AddMulVec.html

※ サンプルのページを右クリックして ページのソースを表示 をクリックすると、全体のコードが見れます。

数値の型

頂点シェーダではfloat以外にベクトルや行列が使えます。
使える数値の型は以下の通りです。

型	説明
float	32bitの浮動小数点数
vec2,vec3,vec4	2,3,4次元のfloatのベクトル
mat2,mat3,mat4	2x2,3x3,4x4のfloatの行列
mat2x2,mat2x3,mat2x4	2x2,2x3,2x4のfloatの行列
mat3x2,mat3x3,mat3x4	3x2,3x3,3x4のfloatの行列
mat4x2,mat4x3,mat4x4	4x2,4x3,4x4のfloatの行列

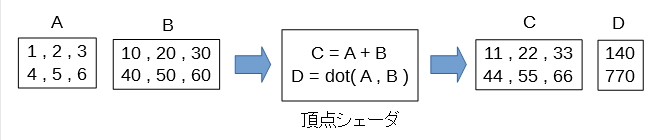
ベクトルの加算と内積

前回の配列の加算と乗算を少し変えて、ベクトルの加算と内積をしてみます。

頂点シェーダのコード

// 入力変数A
in  vec3 A;

// 入力変数B
in  vec3 B;

// 出力変数C
out vec3 C;

// 出力変数D
out float D;

// 要素ごとに呼ばれる関数。
void main(void ) {
    C = A + B;
    D = dot(A, B);
}

入力変数のA,Bと出力変数のCは vec3 として宣言します。

Cの計算式は同じですが、今回は vec3 での加算です。
Dの計算式は内積( dot )になります。

ここでも 入力変数と出力変数の要素の数はすべて同じ という原則は守られています。
A, B, Cは vec3 の要素が2個で、Dは float の要素が2個。
つまりA, B, C, Dはすべて2個の要素を持っています。

サンプルのURL
http://lkzf.info/gpgpu.js/samples/AddDotVec.html

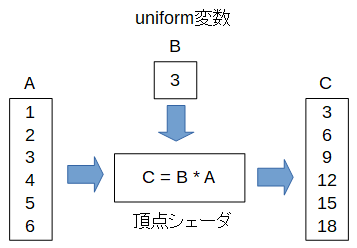
uniform変数

各要素の計算をするときに共通の変数の値を使いたいときは、uniform変数というのを使います。

uniform変数は以下のようにuniformを付けて宣言します。

頂点シェーダのコード

// 入力変数A
in  float A;

// uniform変数B
uniform  float B;

// 出力変数C
out float C;

// 要素ごとに呼ばれる関数。
void main(void ) {
    C = B * A;
}

サンプルのURL
http://lkzf.info/gpgpu.js/samples/UniMul.html

行列とベクトルのかけ算

今度はuniform変数に行列を入れ、入力変数のベクトルとかけ算をしてみます。
実はこれが頂点シェーダの本来の使い方で、3D表示では座標変換行列を頂点の位置ベクトルにかけてスクリーン座標に変換しています。

１つ注意しなければならないのは、WebGLでは[1, 2, 3, 4, 5, 6, 7, 8, 9]の値を3x3の行列(mat3)に入れると、以下のように行列の列ごとに値が入ることです。

    \begin{pmatrix} 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \end{pmatrix}

このような方式をcolumn-major orderと言います。

Cなど他の多くのプログラミング言語はrow-major orderで、その場合は以下のように行列の行ごとに値が入ります。

    \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}

uniform変数Bの行列を入力変数Aの最初のベクトル(1,2,3)をかけると入力変数Cの最初のベクトルは(30,36,42)になります。

    \begin{pmatrix} 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \end{pmatrix}

    \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}

    =
    \begin{pmatrix} 1 * 1 + 4 * 2 + 7 * 3 \\ 2 * 1 + 5 * 2 + 8 * 3 \\ 3 * 1 + 6 * 2 + 9 * 3 \end{pmatrix}

    =
    \begin{pmatrix} 30 \\ 36 \\ 42 \end{pmatrix}

同様に入力変数Aの2番目のベクトル(4,5,6)をかけると入力変数Cの2番目のベクトルは(66,81,96)になります。

    \begin{pmatrix} 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \end{pmatrix}

    \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}

    =
    \begin{pmatrix} 1 * 4 + 4 * 5 + 7 * 6 \\ 2 * 4 + 5 * 5 + 8 * 6 \\ 3 * 4 + 6 * 5 + 9 * 6 \end{pmatrix}

    =
    \begin{pmatrix} 66 \\ 81 \\ 96 \end{pmatrix}

頂点シェーダのコード

// 入力変数A
in  vec3 A;

// uniform変数B
uniform  mat3 B;

// 出力変数C
out vec3 C;

// 要素ごとに呼ばれる関数。
void main(void ) {
    C = B * A;
}

入力変数Aと出力変数Cはvec3, uniform変数Bはmat3です。
Cの計算式は同じですが、今回は行列とベクトルのかけ算になります。

サンプルのURL
http://lkzf.info/gpgpu.js/samples/UniMulMat.html

テクスチャを使った行列の積

uniform変数で使える配列のサイズは数KB～数10KBですので大きなデータを扱いたい場合はテクスチャを使います。

例として以下の行列のかけ算をテクスチャでしてみます。

\begin{pmatrix} 
    1 & 2 & 3 & 4 & 5 & 6 & 7 & 8
    \\ 
    11 & 12 & 13 & 14 & 15 & 16 & 17 & 18
\end{pmatrix}

\begin{pmatrix} 
     1 & 2
    \\ 
     3 & 4
    \\ 
     5 & 6
    \\ 
     7 & 8
    \\ 
     9 & 10
    \\ 
    11 & 12
    \\ 
    13 & 14
    \\ 
    15 & 16
\end{pmatrix}
=
\begin{pmatrix} 372 & 408 \\ 1012 & 1128 \end{pmatrix}

プログラムの構成は以下のようになります。

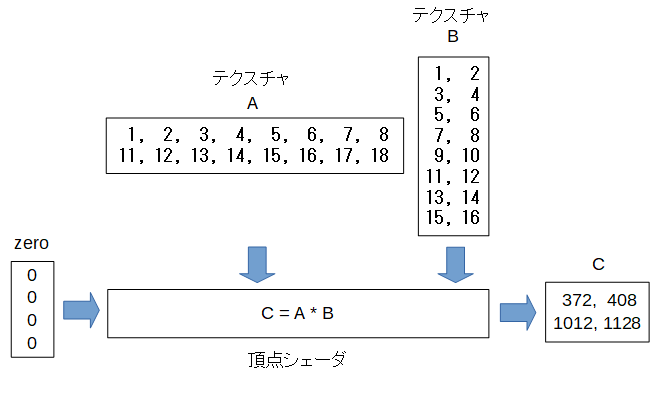
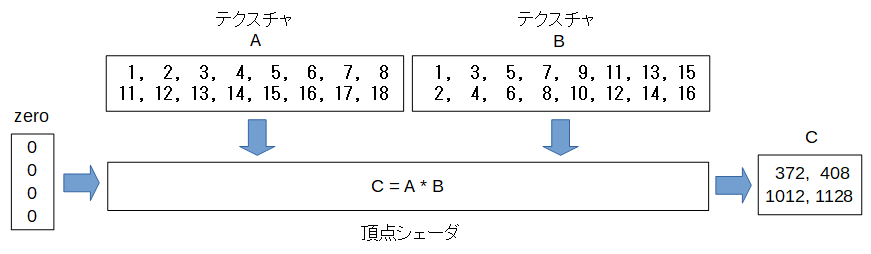
今回は入力変数の値は使わないのですが、 入力変数と出力変数の要素の数は同じ という原則があるので出力変数Cの要素数4と同じサイズの配列で中身の値は0の入力変数zeroを使っています。

頂点シェーダではテクスチャの値を取ってくるのにsamplerというのを使います。

今回のテクスチャは2次元配列なので使うのはsampler2Dです。

頂点シェーダのプログラムはこれまでと比べてかなり長いですが以下の処理をしています。

出力する行列Cの行(row)と列(col)を計算します。
Aのrow行のベクトルとBのcol列のベクトルの内積を計算して出力します。

頂点シェーダのコード

// 入力変数zero。ただし値は使いません。
in float zero;

// 2次元配列のテクスチャ
uniform sampler2D A;
uniform sampler2D B;

// 出力変数C
out float C;

void main() {
    // テクスチャBの行数と列数を取得します。
    // B_sz.yが行数、B_sz.xが列数です。
    ivec2 B_sz = textureSize(B, 0);

    // 出力する行列Cの行(row)と列(col)を計算します。
    // gl_VertexIDは入力変数の何番目の要素かを示すシステム変数です。
    int row = gl_VertexID / B_sz.x;
    int col = gl_VertexID % B_sz.x;

    // Cのrow行col列の値は、Aのrow行のベクトルとBのcol列のベクトルの内積です。

    // 以下のループでベクトルの内積を計算します。
    float sum = 0.0f;
    for(int i = 0; i < B_sz.y; i++) {

        // Aのrow行i列の値を取得します。
        vec4 a = texelFetch(A, ivec2(i, row), 0);

        // Bのi行col列の値を取得します。
        vec4 b = texelFetch(B, ivec2(col, i), 0);

        // a.rとb.rに取得した値が入っています。
        sum += a.r * b.r;
    }

    // 入力変数zeroの値は必要ないですが、使用しない変数はコンパイラが除去してしまいエラーになるので形の上だけ使用します。
    // zeroの値は0なので計算結果には影響しません。
    C = sum + zero;
}

JavaScript側では makeTextureInfo というメソッドを使って、テクスチャの要素の型と行数と列数を指定します。
以下の例ではAはfloatの2行8列のテクスチャ、Bはfloatの8行2列のテクスチャを指定しています。

args: {
    // 出力変数Cと同じサイズで中身の値は0の配列
    "zero": new Float32Array(2 * 2),

    "A": gpgpu.makeTextureInfo("float", [2, 8], A),
    "B": gpgpu.makeTextureInfo("float", [8, 2], B),
    "C": C,
}

テクスチャの要素の型には float,vec2,vec3,vec4 が使えます。

texelFetchはテクスチャの値を vec4 のベクトルに入れて返します。

vec4 の r,g,b,a のフィールドには先頭から順に有効な値が入ります。

テクスチャの要素の型	値が入るフィールド
float	r
vec2	r, g
vec3	r, g, b
vec4	r, g, b, a

なお、テクスチャは2次元と3次元だけで1次元のテクスチャはありません。

1次元のテクスチャを使いたい場合は、1行n列のように2次元のテクスチャで代用します。

また、頂点シェーダで使うmat3やmat4の行列はcolumn-major orderでしたが、テクスチャの行列はrow-major orderなのでご注意ください。

サンプルのURL
http://lkzf.info/gpgpu.js/samples/TexMulMat.html

行列の積の高速化

GPUには多数の計算ユニットがあり計算は高速なのですがメモリの通り道(メモリバス)は1つしかないので、多数の計算ユニットが一斉にメモリ内のあちこちを参照するとたちまち渋滞がおきてしまいます。

頂点シェーダで連続したメモリ領域をアクセスすることにより、ブロック単位でメモリ転送が行われ処理速度の向上が期待できます。

そこでテクスチャBの配置を以下のように変えてみます。

数学的にはBは行と列が入れ替わった転置行列になっています。

こうすると例えばCの1行1列の値は以下のようになり、メモリ内の連続した領域をアクセスするようになりました。

    C_{1,1} = (1, 2, 3, 4, 5, 6, 7, 8) \cdot (1, 3, 5, 7, 9, 11, 13, 15)

テクスチャの値は vec4 として4次元のベクトルとしてアクセスでき、 vec4 の内積を使い以下の計算をしています。

    C_{1,1} = (1, 2, 3, 4) \cdot (1, 3, 5, 7) + (5, 6, 7, 8) \cdot (9, 11, 13, 15)

頂点シェーダのコード


in float zero;

// 2次元配列のテクスチャ
uniform sampler2D A;
uniform sampler2D B;

// 出力変数C
out float C;

void main() {
    // テクスチャBの行数と列数を取得します。
    // B_sz.yが行数、B_sz.xが列数です。
    ivec2 B_sz = textureSize(B, 0);

    // 出力する行列Cの行(row)と列(col)を計算します。
    // gl_VertexIDは入力変数の何番目の要素かを示すシステム変数です。
    int row = gl_VertexID / B_sz.y;
    int col = gl_VertexID % B_sz.y;

    // Cのrow行col列の値は、Aのrow行のベクトルとBのcol行のベクトルの内積です。

    // 以下のループでベクトルの内積を計算します。
    float sum = 0.0f;
    for(int i = 0; i < B_sz.x; i++){

        // Aのrow行i列の値を取得します。
        vec4 a = texelFetch(A, ivec2(i, row), 0);

        // Bのcol行i列の値を取得します。
        // !!!!! 前回はi行col列なので ivec2(col, i) でした。   !!!!!
        // !!!!! 今回は転置したので行と列が入れ替わっています。!!!!!
        vec4 b = texelFetch(B, ivec2(i, col), 0);

        sum += dot(a, b);
    }

    // 入力変数zeroの値は必要ないですが、使用しない変数はコンパイラが除去してしまいエラーになるので形の上だけ使用します。
    // zeroの値は0なので計算結果には影響しません。
    C = sum +zero;
}

以下はJavaScript側でBの値をセットするコードです。

前回のサンプルでは [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16] を入れていました。
今回は値を転置して入れています。

var B = new Float32Array([1, 3, 5, 7, 9, 11, 13, 15, 2, 4, 6, 8, 10, 12, 14, 16]);

サンプルのURL
http://lkzf.info/gpgpu.js/samples/TexMulMatVec4.html

スピードテスト

2つの行列の積の計算速度をさまざまな方法で比較してみました。

テスト環境

以下のPCを使いました。

OS
Windows10 64bit
CPU
Core i7-6700 3.4GHz メモリ:8GB キャッシュメモリ:8MB 論理コア:8個
GPU
GeForce GTX 1070 1.5GHz メモリ:8GB CUDAコア:1920個

計算方法

5種類の計算方法でテストしました。
以降のグラフの凡例に表示される言葉の意味は以下のとおりです。

JavaScript
WebGLを使わずJavaScriptだけで計算しました。
gpgpu.js
テクスチャを使った行列の積 で説明した方法です。
高速化
行列の積の高速化 で説明した方法です。
C++
OpenMPを使って並列処理をしました。
CUDA
元祖GPGPU。 NVIDIAのGPUで使えます。

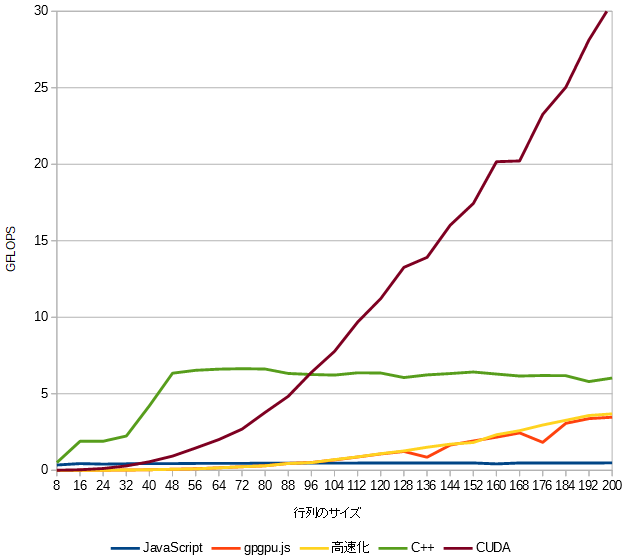
行列サイズ200までのグラフ

8x8から200x200までのサイズの行列の積の計算速度(GFLOPS)をプロットしました。

このグラフを見ると行列サイズが96以降でCUDAは最速ですが、行列サイズが36以下だとJavaScriptよりも遅いです。

gpgpu.jsは行列サイズが90ぐらいからJavaScriptよりも速くなっています。

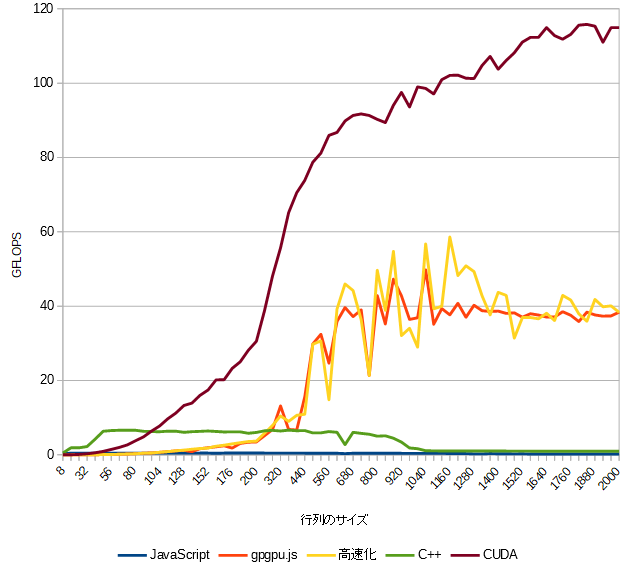
行列サイズ2000までのグラフ

このグラフではCUDAが相変わらず速く、それにgpgpu.jsが続きます。

gpgpu.jsの高速化はそれほど効果がないように見えます。

C++は行列サイズが1000あたりから急に速度が落ちています。

2個の1000x1000のfloatの行列をかけ算するときのメモリサイズは 2 * 4 * 1000 * 1000 = 8MB です。

Core i7-6700のキャッシュメモリは8MBなのでキャッシュメモリの限界かもしれません。

C++のコードの改善

以下は行列の積 C = A ・ B のC++のコードです。

    #pragma omp parallel for
    for (int row = 0; row < size; row++) {
        for (int col = 0; col < size; col++) {
            float sum = 0.0f;
            for (int i = 0; i < size; i++) {
                sum += A[row * size + i] * B[i * size + col];
            }
            C[row * size + col] = sum;
        }
    }

sumを計算する i のforループで B[i * size + col] を参照していますが、
i が1つカウントアップすると size だけ離れたメモリをアクセスします。

size が2000だとかなり離れた場所になります。

そこで BT をBの転置行列 $ B^T $ として以下のコードに変更してみます。

こうすると i をカウントアップしたときに BT[col * size + i] は連続したメモリ領域になります。

    #pragma omp parallel for
    for (int row = 0; row < size; row++) {
        for (int col = 0; col < size; col++) {
            float sum = 0.0f;
            for (int i = 0; i < size; i++) {
                sum += A[row * size + i] * BT[col * size + i];
            }
            C[row * size + col] = sum;
        }
    }

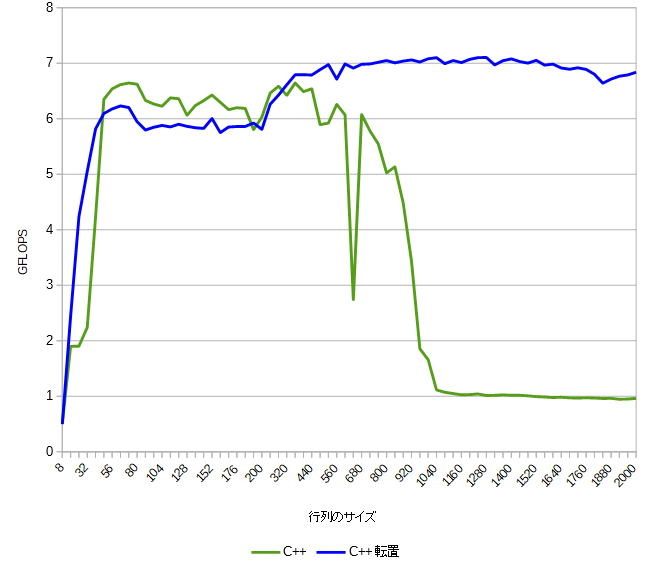
変更後のC++のグラフ

明らかに転置の効果が出ています。

C++では転置の効果が顕著なのに、gpgpu.jsでは転置の効果がないのは GeForce のキャッシュメモリが優秀で飛び飛びのメモリにアクセスしてもキャッシュメモリが対応してくれているのかもしれません。

NVIDIA以外のGPUのテスト

CUDAが使えないNVIDIA以外のGPUのテストをしてみます。

OS
Windows10 64bit
CPU
Core i5-6200U 2.3GHz メモリ:8GB 論理コア:4個
GPU
CPU内蔵 Intel HD Graphics 520 1.5GHz

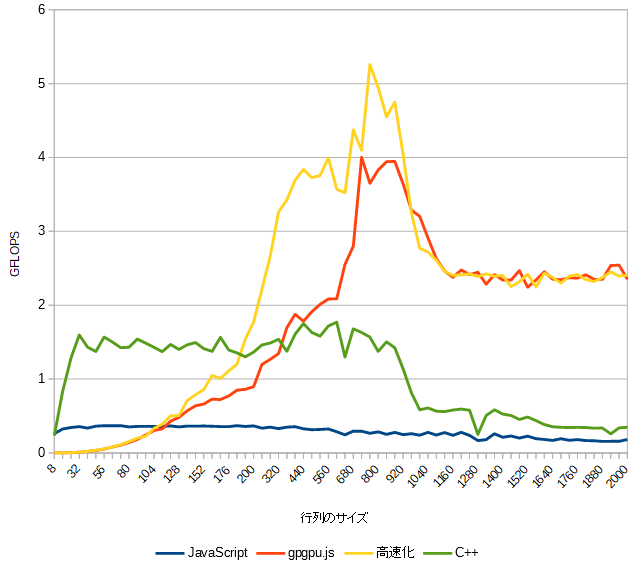
NVIDIA以外のGPUのグラフ

こちらではgpgpu.jsで高速化の効果が見れます。

CPU内蔵のGPUのキャッシュメモリは GeForce ほど優秀ではないからかも知れません。

C++はやはり行列のサイズが大きいと速度が落ちています。(変更前のコードでテストしています。)

今後の予定

ディープラーニング

元々はブラウザでディープラーニングをするためにWebGL 2.0を使ってGPGPUのプログラムを書いていました。
CNN(畳み込みニューラルネットワーク)を使ったMNISTの文字認識で正解率は99%です。

ソースを整理してからこちらの記事も書いてみたいと思います。

ディープラーニングのURL
http://lkzf.info/gpgpu.js/DeepLearning/MNIST.html

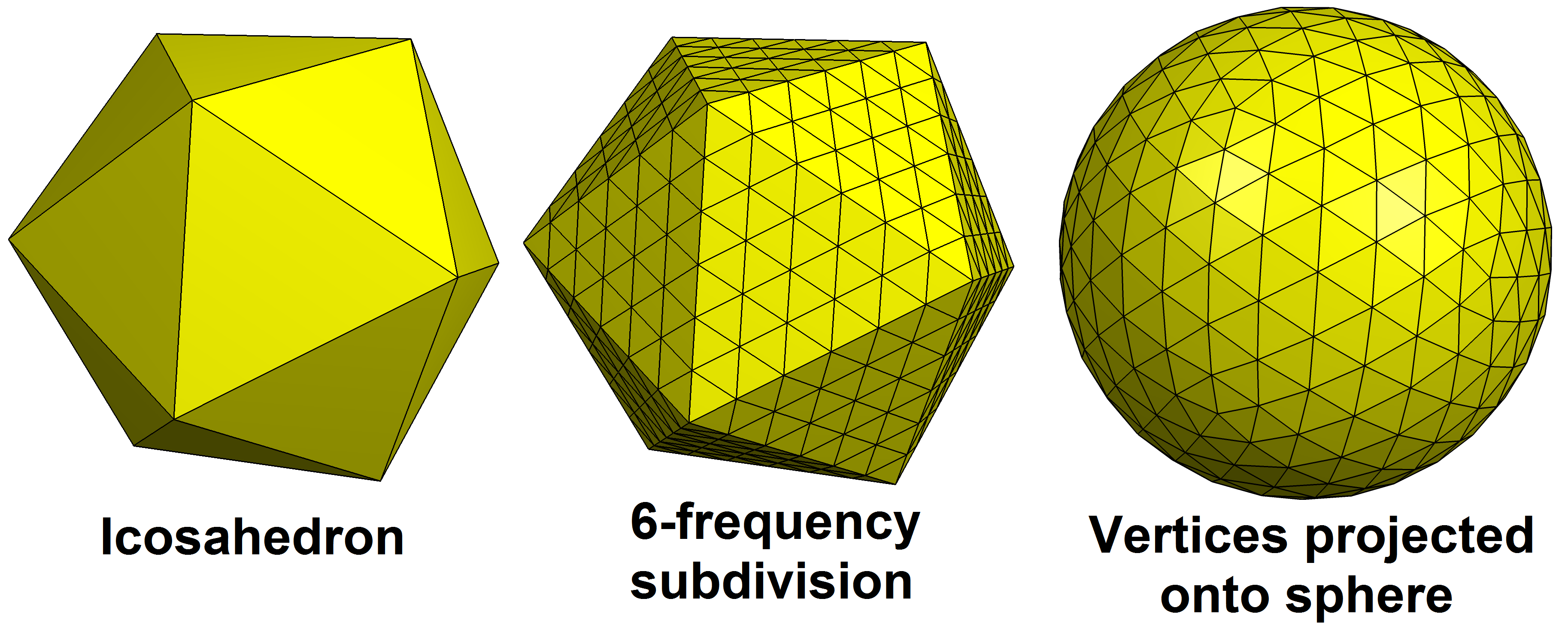
地球シミュレータ

シミュレーションをするには球面を均等に分割する必要があり、それにはGeodesic polyhedronという方法があります。

こちらのページが参考になりました。

Geodesic polyhedron
https://en.wikipedia.org/wiki/Geodesic_polyhedron

Spherical geodesic grids
http://kiwi.atmos.colostate.edu/rr/groupPIX/ross/ross1/ross1.html

現在Geodesic polyhedronを作るところまではできました。
マウスでグリグリ動かせます。
http://lkzf.info/gpgpu.js/samples/earth.html

こちらもソースを整理してから記事を書いてみたいと思います。

おわりに

誤りや勘違いしているところがあればご指摘していただければ助かります。

つたない文章をここまで読んでくださり、ありがとうございました。

JavaScriptのWebGL 2.0でGPGPU

はじめに

WebGL 2.0でのGPGPUのしくみ

配列の加算

配列の加算と乗算

頂点シェーダのコード

数値の型

ベクトルの加算と内積

頂点シェーダのコード

uniform変数

頂点シェーダのコード

行列とベクトルのかけ算

頂点シェーダのコード

テクスチャを使った行列の積

頂点シェーダのコード

行列の積の高速化

頂点シェーダのコード

スピード テスト

テスト環境

計算方法

行列サイズ200までのグラフ

行列サイズ2000までのグラフ

C++のコードの改善

変更後のC++のグラフ

NVIDIA以外のGPUのテスト

NVIDIA以外のGPUのグラフ

今後の予定

ディープラーニング

地球シミュレータ

おわりに

スピードテスト