機械学習の流れ

データ分析を行うにあたり、以下の流れでデータの分析及び予測を行う。
1.課題の設定（どのような課題を解決したいか）
2.データ選定及び収集（Excelファイル、スクレイピング等）
3.データ加工、前処理（正規化、欠損処理等）
4.モデル選定（どのモデルが適切か、多岐に渡る手法から選ぶ）
5.モデル学習（パラメータを調整する）
6.モデル評価（モデルの精度を測る）
本記事では4.を中心に記述する。

機械学習の手法について

機械学習の手法について、大きく３つに分けられる。

1.教師あり学習
2.教師なし学習
3.強化学習

今回は統計的手法に基づく、教師あり学習と教師なし学習について記載する。

教師あり学習

教師あり学習とは、学習データにラベルを付けて学習する方法のことである。
例えば、犬の画像には犬、猫の画像には猫のラベルを付与して大量の画像を用意する。その画像データを学習し、新たな犬の画像を適用した時に犬の画像と判断することが挙げられる。

教師あり学習には以下の２つのタスクに分けられる。
1.回帰
回帰とは、ある入力データからある出力データ（連続値）を予測する問題のことである。
機械学習で回帰を行う際に用いられる手法は以下の通りである。

線形回帰（単回帰、重回帰）
非線形回帰

2.分類
分類とは、先ほどの画像の例のように、出力データをクラス分類（上記の例では犬と猫の２値分類）で予測する問題のことである。
機械学習で分類を行う際に用いられる手法は以下の通りである。

ロジスティック回帰
サポートベクターマシン
決定木
k-近傍法

教師なし学習

教師なし学習とは、学習データにラベルを付与せず学習する方法のことである。
例えば、先ほどとは異なりラベルを付与していない大量の犬と猫の画像を用意する。その画像データを学習し、画像の特徴から犬と猫のグループ分けを行うことが挙げられる。

教師なし学習には以下の２つのタスクにわけられる。
1.クラスタリング
クラスタリングとは、上記の教師なし学習の例のようにラベルのついていないデータから特徴を見つけて、グループに分けることである。
クラスタリングに用いられる手法は以下の通りである。

k-means法

2.次元削減
次元削減とは、機械学習では高次元のデータを扱うため計算コストを減らすためにデータの圧縮を行うことである。
次元削減に用いられる手法は以下の通りである。

主成分分析（PCA）

各代表的な手法について要点をまとめる。

線形回帰モデル

目的変数を説明変数とパラメータの内積の線形結合と切片を足し合わせてモデルを作成する
モデルのパラメータは最小二乗法で推定し算出される
説明変数が１次元の時は単回帰モデルと呼び、多次元の場合は重回帰モデルと呼ぶ
モデルの検証はMAEまたはMSEやR2で評価することが多い

ハンズオン
ボストンの住宅価格予測

線形回帰モデル

# 説明変数
data = df.loc[:, ['RM']].values
# 目的変数
target = df.loc[:, 'PRICE'].values
## sklearnモジュールからLinearRegressionをインポート
from sklearn.linear_model import LinearRegression
# オブジェクト生成
model = LinearRegression()
# fit関数でパラメータ推定
model.fit(data, target)
# 回帰係数と切片を出力
model.coef_
model.intercept_
}

coef_：9.10210898
intercept_：-34.67062077643857

線形回帰モデル（学習と検証に分割）

# 説明変数
data = df.loc[:, ['RM']].values
# 目的変数
target = df.loc[:, 'PRICE'].values
## sklearnモジュールからLinearRegressionをインポート
from sklearn.linear_model import LinearRegression
# train_test_splitをインポート
from sklearn.model_selection import train_test_split
# 70%を学習用、30%を検証用データにするよう分割
X_train, X_test, y_train, y_test = train_test_split(data, target, 
test_size = 0.3, random_state = 666)
# 学習用データでパラメータ推定
model.fit(X_train, y_train)
# 作成したモデルから予測（学習用、検証用モデル使用）
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
# 回帰係数と切片を出力
print(model.coef_)
print(model.intercept_)
# 平均二乗誤差を評価するためのメソッドを呼び出し
from sklearn.metrics import mean_squared_error
# 学習用、検証用データに関して平均二乗誤差を出力
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
# 学習用、検証用データに関してR^2を出力
print('R^2 Train : %.3f, Test : %.3f' % (model.score(X_train, y_train), model.score(X_test, y_test)))

coef_：9.23560156
intercept_：-35.48090633823544
MSE Train : 44.983, Test : 40.412
R^2 Train : 0.500, Test : 0.434

重回帰モデル

# 説明変数
data2 = df.loc[:, ['CRIM', 'RM']].values
# 目的変数
target2 = df.loc[:, 'PRICE'].values
## sklearnモジュールからLinearRegressionをインポート
from sklearn.linear_model import LinearRegression
# train_test_splitをインポート
from sklearn.model_selection import train_test_split
# 70%を学習用、30%を検証用データにするよう分割
X_train, X_test, y_train, y_test = train_test_split(data2, target2, 
test_size = 0.3, random_state = 666)
# 学習用データでパラメータ推定
model.fit(X_train, y_train)
# 作成したモデルから予測（学習用、検証用モデル使用）
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
# 回帰係数と切片を出力
print(model.coef_)
print(model.intercept_)
# 平均二乗誤差を評価するためのメソッドを呼び出し
from sklearn.metrics import mean_squared_error
# 学習用、検証用データに関して平均二乗誤差を出力
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
# 学習用、検証用データに関してR^2を出力
print('R^2 Train : %.3f, Test : %.3f' % (model.score(X_train, y_train), model.score(X_test, y_test)))

coef_：-0.24083902 　8.59266849
intercept_：-30.54299163779955
MSE Train : 40.586, Test : 34.377
R^2 Train : 0.549, Test : 0.518

考察

sklearnを用いるとプログラムが非常にシンプルになる
今回のケースでは重回帰モデルの方が誤差が少なく、決定係数が高いた説明に適しているモデルと言える

非線形回帰モデル

複雑な現象に関して、非線形モデルで表現する
目的変数を、基底関数と呼ばれる既知の非線形関数とパラメータベクトルの線型結合を使用
パラメータは最小二乗法や最尤法で推定（線形回帰モデルと同様）
基底関数として、多項式関数やガウス型基底関数を用いる

バイアスとバリアンス

高バイアス-低バリアンス：予測モデルが大きく変わらないが、誤差 (真の値とのズレ)が大きい。未学習と呼ばれる。
低バイアス-高バリアンス：予測モデルが大きく変わるが、誤差は小さい、過学習と呼ばれる。
バイアスとバリアンスはトレードオフの関係にあり、適切な表現力のモデルを作成することが重要である。
過学習を抑えるための一つの手法として、正則化がある。

モデルの検証について

ホールドアウト法：学習データと検証データを一定の割合で分割し、検証する方法。時系列データで用いられることが多い。
交差検証法：学習データと検証データを分割し、組み合わせを変えることで全てのデータを学習および検証に用いることが出来る。

ロジスティック回帰モデル

分類問題を解くために用いられるモデル
目的変数を、クラス値（２値分類）にするために、シグモイド関数を使用
パラメータは最尤法で推定する
尤度関数を最大化するために、勾配降下法を用いる
モデルの評価は混同行列やacuuracyやAUCを用いる

ハンズオン
タイタニックの生存確率

ロジスティック回帰モデル（説明変数が運賃のみ）

#運賃だけのリストを作成
data1 = titanic_df.loc[:, ["Fare"]].values
#生死フラグのみのリストを作成
label1 =  titanic_df.loc[:,["Survived"]].values
# 学習データと検証データを分割
from sklearn.model_selection import train_test_split
traindata1, testdata1, trainlabel1, testlabel1 = train_test_split(data1, label1, test_size=0.2)
#モデルの学習
eval_model1=LogisticRegression()
predictor_eval1=eval_model1.fit(traindata1, trainlabel1).predict(testdata1)
#モデルの評価
eval_model1.score(traindata1, trainlabel1)
#混同行列の作成
from sklearn.metrics import confusion_matrix
confusion_matrix1=confusion_matrix(testlabel1, predictor_eval1)

accuracy：0.672752808988764

ロジスティック回帰モデル（説明変数が運賃と性別）

# Genderの項目を加工して予測に用いる
titanic_df['Gender'] = titanic_df['Sex'].map({'female': 0, 'male': 1}).astype(int)
titanic_df['Pclass_Gender'] = titanic_df['Pclass'] + titanic_df['Gender']
titanic_df = titanic_df.drop(['Pclass', 'Sex', 'Gender','Age'], axis=1)
#運賃とGenderのリストを作成
data2 = titanic_df.loc[:, ["AgeFill", "Pclass_Gender"]].values
#生死フラグのみのリストを作成
label2 =  titanic_df.loc[:,["Survived"]].values
# 学習データと検証データを分割
from sklearn.model_selection import train_test_split
traindata2, testdata2, trainlabel2, testlabel2 = train_test_split(data2, label2, test_size=0.2)
#モデルの学習
eval_model2=LogisticRegression()
predictor_eval2=eval_model2.fit(traindata2, trainlabel2).predict(testdata2)
#モデルの評価
eval_model2.score(traindata2, trainlabel2)
#混同行列の作成
from sklearn.metrics import confusion_matrix
confusion_matrix2=confusion_matrix(testlabel2, predictor_eval2)

accuracy：0.7668539325842697

考察

ロジスティック回帰を用いるために前処理を行うことが重要である
今回のケースでは、変数を増やしたほうが制度が良いモデルを作成することが出来た

主成分分析

教師なし学習の次元削減のために用いられる手法
多次元データをなるべく情報量を保ちながら次元数を減らす
学習データの分散が最大になる方向に線形変換する

乳がん検査データを用いたロジスティック回帰

# 説明変数の抽出
X = cancer_df.loc[:, 'radius_mean':]
# 目的変数の抽出
y = cancer_df.diagnosis.apply(lambda d: 1 if d == 'M' else 0)
# 学習用とテスト用でデータを分離
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# 標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# ロジスティック回帰で学習
logistic = LogisticRegressionCV(cv=10, random_state=0)
logistic.fit(X_train_scaled, y_train)

# 検証
print('Train score: {:.3f}'.format(logistic.score(X_train_scaled, y_train)))
print('Test score: {:.3f}'.format(logistic.score(X_test_scaled, y_test)))
print('Confustion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=logistic.predict(X_test_scaled))))

Train score: 0.988
Test score: 0.972
Confustion matrix:
[[89 1]
[ 3 50]]

乳がん検査データを用いたロジスティック回帰（主成分分析で次元数を２にした場合）

# 説明変数の抽出
X = cancer_df.loc[:, 'radius_mean':]
# 目的変数の抽出
y = cancer_df.diagnosis.apply(lambda d: 1 if d == 'M' else 0)

# PCA
# 次元数2まで圧縮
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

# 寄与率
print('explained variance ratio: {}'.format(pca.explained_variance_ratio_))

# 学習用とテスト用でデータを分離
X_train, X_test, y_train, y_test = train_test_split(X_pca, y, random_state=0)

# 標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# ロジスティック回帰で学習
logistic = LogisticRegressionCV(cv=10, random_state=0)
logistic.fit(X_train_scaled, y_train)

# 検証
print('Train score: {:.3f}'.format(logistic.score(X_train_scaled, y_train)))
print('Test score: {:.3f}'.format(logistic.score(X_test_scaled, y_test)))
print('Confustion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=logistic.predict(X_test_scaled))))

explained variance ratio: [0.98204467 0.01617649]
Train score: 0.920
Test score: 0.944
Confustion matrix:
[[88 2]
[ 6 47]]

考察

精度を保ちながら次元数を２に減らし、分類問題を予測することが出来た
今回のケースでは次元数が数十個だったため計算コストの削減を実感出来なかったが、さらに高次元だと有効になるのではないかと感じた

アルゴリズム

k-近傍法

分類問題に用いる手法
予測するデータ点との距離が最も近い 𝑘 個の訓練データのラベルの最頻値を割り当てる

k-means

教師なし学習のクラスタリングに用いる手法
与えられたデータをk個のクラスタに分類する
初期値によって結果が変わるため、何回か繰り返す必要がある

サポートベクターマシン

教師あり学習の回帰や分類に用いられる手法
線形判別関数ともっとも近いデータ点との距離であるマージンが最大となる関数を求める

タイタニックの生存確率

サポートベクターマシンとロジスティック回帰の比較

#モデルの学習
from sklearn.svm import SVC
SVC_model1=SVC()
predictor_eval1=SVC_model1.fit(traindata1, trainlabel1).predict(testdata1)
#モデルの評価
SVC_model1.score(traindata1, trainlabel1)
#混同行列の作成
from sklearn.metrics import confusion_matrix
confusion_matrix1=confusion_matrix(testlabel1, predictor_eval1)

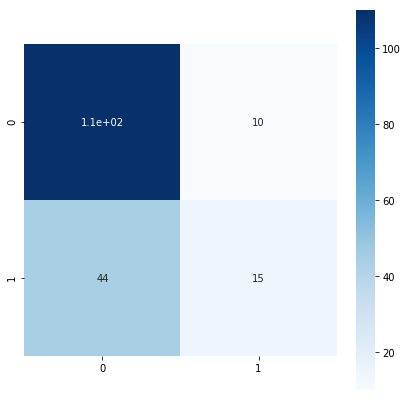
ロジスティック回帰
accuracy：0.6587078651685393
array([[105, 8],
[ 49, 17]])

サポートベクターマシン
accuracy：0.7542134831460674
array([[86, 27],
[33, 33]])

サポートベクターマシンとロジスティック回帰の比較（運賃と性別）

#モデルの学習
from sklearn.svm import SVC
SVC_model2=SVC()
predictor_eval2=SVC_model2.fit(traindata2, trainlabel2).predict(testdata2)
#モデルの評価
SVC_model2.score(traindata2, trainlabel2)
#混同行列の作成
from sklearn.metrics import confusion_matrix
confusion_matrix2=confusion_matrix(testlabel2, predictor_eval2)

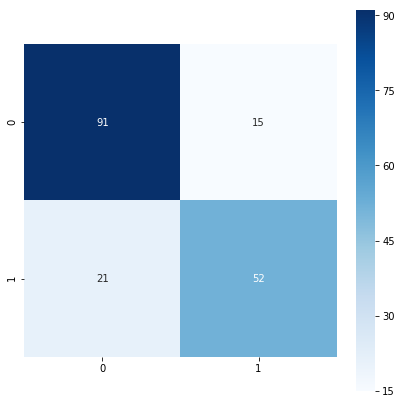
ロジスティック回帰
accuracy：0.7879213483146067
array([[94, 13],
[32, 40]])

サポートベクターマシン
accuracy：0.8216292134831461
array([[96, 11],
[32, 40]])

考察

今回のケースではロジスティック回帰モデルよりもサポートベクターマシンの方が精度が高い
sklearnを用いると様々なモデルの比較が容易に行える

【E資格】part2 機械学習レポート

機械学習の流れ

機械学習の手法について

教師あり学習

教師なし学習

線形回帰モデル

線形回帰モデル

線形回帰モデル（学習と検証に分割）

重回帰モデル

非線形回帰モデル

バイアスとバリアンス

モデルの検証について

ロジスティック回帰モデル

ロジスティック回帰モデル（説明変数が運賃のみ）

ロジスティック回帰モデル（説明変数が運賃と性別）

主成分分析

乳がん検査データを用いたロジスティック回帰

乳がん検査データを用いたロジスティック回帰（主成分分析で次元数を２にした場合）

アルゴリズム

k-近傍法

k-means

サポートベクターマシン

サポートベクターマシンとロジスティック回帰の比較

サポートベクターマシンとロジスティック回帰の比較（運賃と性別）