LoginSignup
0
1

More than 3 years have passed since last update.

@teatake

【E資格】part5 深層学習Day3

Posted at

深層学習 Day3

本記事はラビット☆チャレンジのレポートとして記載し、今回は以下の内容について記述する。

Section1：再帰型ニューラルネットワークの概念
Section2：LSTM
Section3：GRU
Section4：双方向RNN
Section5：Seq2Seq
Section6：Word2Vec
Section7：AttentionMechanism

動画の要約

Section1：再帰型ニューラルネットワークの概念

1) RNNとは

  • 時系列データに対応可能なニューラルネットワーク

2) 時系列データとは

  • 時間的順序を追って一定間隔ごとに観察され，しかも相互に統計的依存関係が認められるようなデータ
    • 音声データ
    • テキストデータ
    • 株価のデータ等

3) RNNの特徴

  • 初期の状態と過去の時間t-1の状態を保持して時系列データを扱う
  • 次の時間でのtを再帰的に求める再帰構造を持つ

4) BPTT

  • Backpropagation Through Time
  • RNNにおいてのパラメータ調整方法の一種（誤差逆伝播法の一種）

Section2：LSTM

1) RNNの問題点

課題：時系列を遡れば遡るほど、勾配が消失していくので長い時系列の学習が困難
解決策：RNNの構造自体を変えてLSTMという手法を用いる

2) CEC

  • constant error carousel
  • RNNの問題である勾配消失および勾配爆発の解決方法として、勾配が1であれば解決できる

課題：入力データについて、時間依存度に関係なく重みが一律であり、ニューラルネットワークの学習特性が無い

3) 入力ゲートと出力ゲート

  • 入力・出力ゲートを追加することで入力値の重みを、重み行列で可変可能
  • 上記の対応でCECの課題が解決

4) 忘却ゲート

  • 過去の情報が要らなくなった場合、そのタイミングで情報を忘却する忘却ゲートの誕生
  • 過去の情報が全て保管されていて、不要になった場合でも削除できないCECの課題を解決

5) 覗き穴結合

  • CEC自身の値に、重み行列を介して伝播可能にした構造
  • CECに保存されている過去の情報を任意のタイミングで他のノードに伝播させたり、忘却させることで、CECの課題を解決

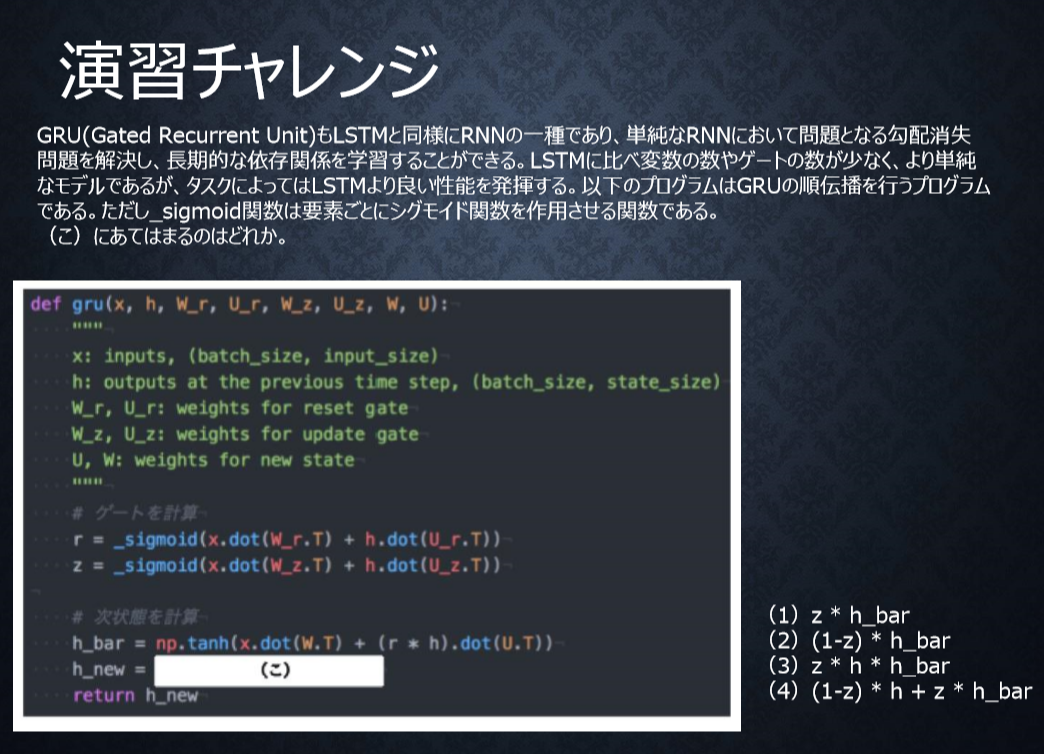
Section3：GRU

  • GRU(Gated Recurrent Unit) とはLSTMのパラメータを大幅に削減し単純化したモデル
  • パラメータ数が多く、計算負荷が高いというLSTMの課題に対応
  • LSTMと同等またはそれ以上の精度が望める構造

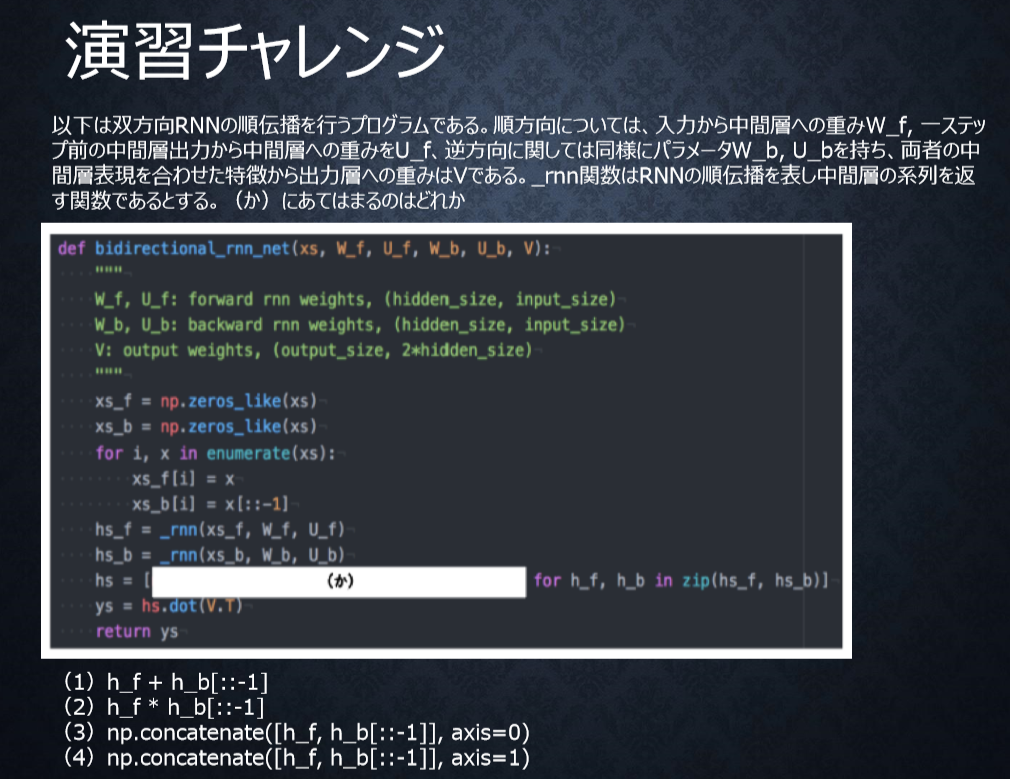
Section4：双方向RNN

  • 過去の情報だけでなく、未来の情報を加味することで、精度を向上させるためのモデル
  • 実用例
    • 文章の推敲
    • 機械翻訳等

Section5：Seq2Seq

  • 機械対話や、機械翻訳などに使用されている
  • Encoder-Decoderモデルの一種

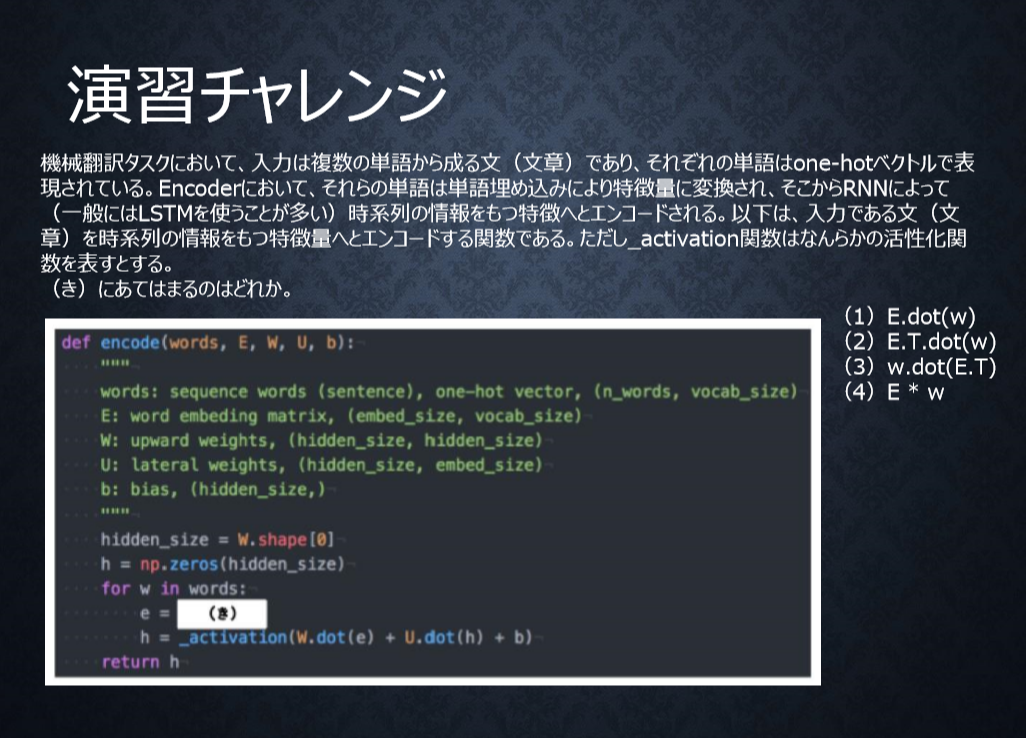
1) Encoder RNN

  • 入力テキストデータを、単語等のトークンに区切って渡す構造
  • Taking :文章を単語等のトークン毎に分割し、トークンごとのIDに分割
  • Embedding :ID から、そのトークンを表す分散表現ベクトルに変換
  • Encoder RNN:ベクトルを順番にRNNに入力していく
  • 最後に入力したときの出力結果をとっておき、Decoder RNNへ渡す

2) Decoder RNN

  • システムがアウトプットデータを、単語等のトークンごとに生成する構造
  • Decoder RNN: Encoder RNN の出力結果から、各 token の生成確率を出力する
  • Sampling: 生成確率にもとづいて token をランダムに選ぶ
  • Embedding: 選ばれた token を Embedding して Decoder RNN への次の入力とする
  • Detokenize: 上記を繰り返し、得られた token を文字列に直す

3) HRED

  • 過去 n-1 個の発話から次の発話を生成する
  • Seq2Seq + Context RNNの構成を持つ
  • 過去の発話の履歴を加味した返答ができる
  • 問に対して文脈も何もなく、ただ応答が行われる一問一答形式のSeq2Seqの課題に対応

4) VHRED

  • HREDに、VAEの潜在変数の概念を追加したもの
  • HREDの課題
    • HRED は確率的な多様性が字面にしかなく、会話の「流れ」のような多様性が無い
    • HRED は短く情報量に乏しい答えをしがち
  • VAEの潜在変数の概念を追加することで上記課題を解決した構造

5) オートエンコーダー

  • 教師なし学習の一つ
  • 次元削減が行えることが利点
  • Encoder: 入力データから潜在変数zに変換するNN
  • Decoder: 潜在変数zをインプットとして入力データを復元するNN

6) VAE

  • Variational AutoEncoder
  • 潜在変数$z$に確率分布$z∼N(0,1)$を仮定したもの
  • 通常のオートエンコーダーの場合、潜在変数$z$の構造がどのような状態かわからない

Section6：Word2Vec

  • 学習データからボキャブラリを作成
  • 大規模データの分散表現の学習が、現実的な計算速度とメモリ量で実現可能にした
  • one-hotベクトルでボキャブラリを表現
  • RNNには単語のような可変長の文字列をNNに与えることはできないため、上記方法により固定長で表現可能

Section7：AttentionMechanism

  • 「入力と出力のどの単語が関連しているのか」の関連度を学習する仕組み
  • seq2seq は長い文章への対応が難しい、という課題に対応

確認テスト

P11 サイズ5×5の入力画像を、サイズ3×3のフィルタで 畳み込んだ時の出力画像のサイズを答えよ。なおストライドは2、パディングは1とする。

＜答え＞
3×3

\begin{eqnarray}
OH &=& \frac{入力サイズ(H)+2 \times パディング - フィルタサイズ(H)}{ストライド}+1
\\ &=& \frac{5+2 \times 1 - 3}{2}+1
\\ &=& 3
\end{eqnarray}

\begin{eqnarray}
OW &=& \frac{入力サイズ(W)+2 \times パディング - フィルタサイズ(W)}{ストライド}+1
\\ &=& 3
\end{eqnarray}

P23 RNNのネットワークには大きくわけて3つの重みがある。1つは入力から現在の中間層を定義する際にかけられる重み、1つは中間層から出力を定義する際にかけられる重みである。残り1つの重みについて説明せよ
＜答え＞
一つ前の中間層の出力を、次の中間層の入力にする際にかけられる重み

P37 連鎖律の原理を使い、$\frac{dz}{dx}$を求めよ

z = t^2,t = x+y

＜答え＞
連鎖律を用いて計算する。

\frac{dz}{dx} =\frac{dz}{dt} \frac{dt}{dx}=2t \cdot 1 =2t=2(x+y)

P44.　下図の$y_1$ を $x,s_0,s_1,w_{in},w,w_{out}$を用いて数式で表せ。
※バイアスは任意の文字で定義せよ。（今回は$b,c$をバイアスとした）
※また中間層の出力にシグモイド関数 $g(x)$ を作用させよ。

b.png

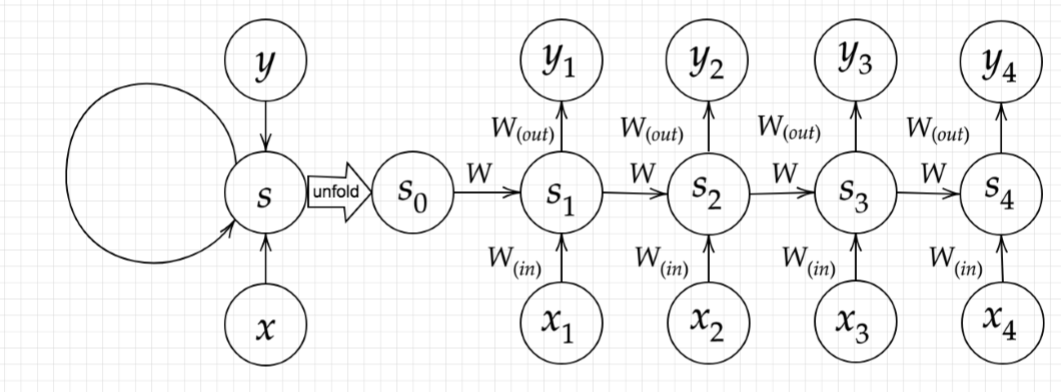
＜答え＞

\begin{eqnarray}
y_1 &=& g(s_1 \cdot w_{out}+c)
\\ s_1 &=& g(s_0 \cdot w + x_1 \cdot w_{in} +b)
\end{eqnarray}

P63 シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値として正しいものを選択肢から選べ。
（1）0.15
（2）0.25
（3）0.35
（4）0.45
＜答え＞
(2)

f(x) = \frac{1}{1+e^{-x}}

f^{\prime}(x) = (1-f(x))\cdot f(x)

f^{\prime}(0) = (1-f(0))\cdot f(0)= 2^{-2} = 0.25

P79 以下の文章をLSTMに入力し空欄に当てはまる単語を予測したいとする。 文中の「とても」という言葉は空欄の予測においてなくなっても影響を及ぼさないと考えられる。 このような場合、どのゲートが作用すると考えられるか。
＜文章＞
「映画おもしろかったね。ところで、とてもお腹が空いたから何か____。」

＜答え＞
忘却ゲート

P89 LSTMとCECが抱える課題について、それぞれ簡潔に述べよ。

＜答え＞
LSTM：パラメータが多い。計算量が多い。
CEC：勾配が１のため、重みがなくなり学習が行えない

P93 LSTMとGRUの違いを簡潔に述べよ。

＜答え＞
LSTM：パラメータが多い。計算負荷が大きい。
GRU：パラメータが少ない。計算負荷が少ない。

P63
下記の選択肢から、seq2seqについて説明しているものを選べ。

  1. 時刻に関して順方向と逆方向のRNNを構成し、それら2つの中間層表現を特徴量として利用 するものである。
  2. RNNを用いたEncoder-Decoderモデルの一種であり、機械翻訳などのモデルに使われる。
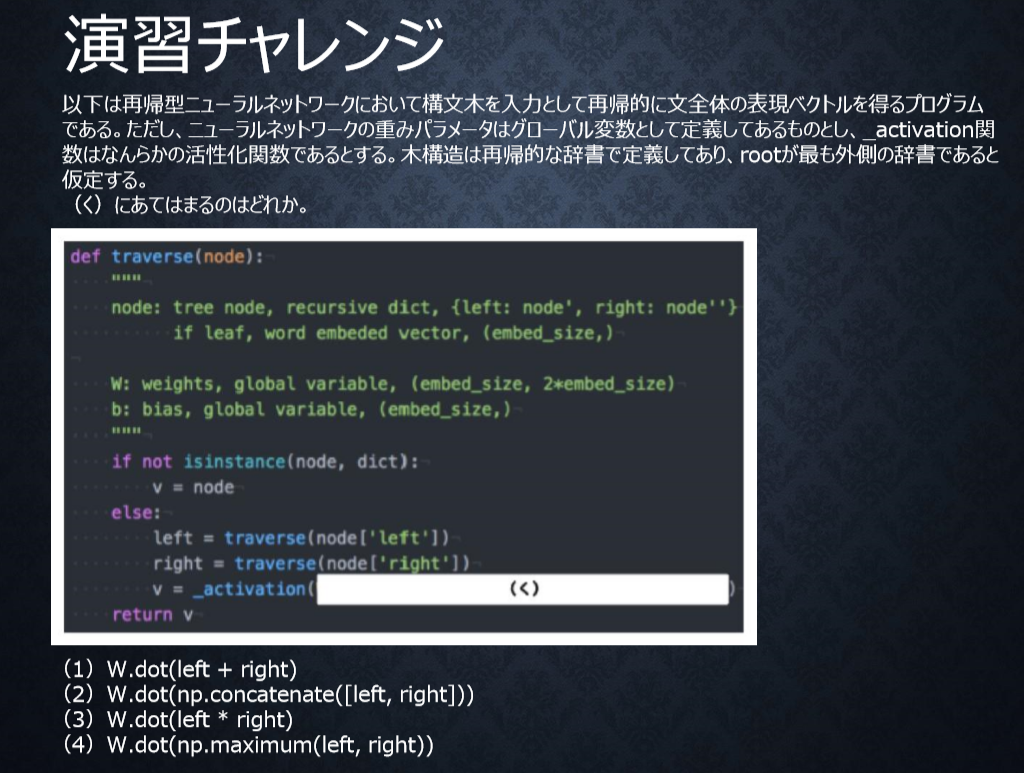
  3. 構文木などの木構造に対して、隣接単語から表現ベクトル（フレーズ）を作るという演算を再帰的に行い（重みは共通）、文全体の表現ベクトルを得るニューラルネットワークである。
  4. RNNの一種であり、単純なRNNにおいて問題となる勾配消失問題をCECとゲートの概念を導入することで解決したものである。

＜答え＞
2

P120 seq2seqとHRED、HREDとVHREDの違いを簡潔に述べよ。

seq2seq： 一問一答。問に対して文脈も何もなく、ただ応答が行われる
HRED： 前の単語の流れに即して応答される。毎回同じ回答になる
VHRED：文脈に則した、異なる回答を行う

P100 VAEに関する下記の説明文中の空欄に当てはまる言葉を答えよ。
自己符号化器の潜在変数に____を導入したもの

＜答え＞
確率分布

P138 RNNとword2vec、seq2seqとAttentionの違いを簡潔に述べよ。

RNN：ボキャブラリ×ボキャブラリの数の重み行列が必要
word2vec：ボキャブラリ×任意のwordで重み行列を作成
seq2seq：固定次元ベクトルのものしか学習できない。長い文章への対応が難しい
Attention：長い文章でも対応可能

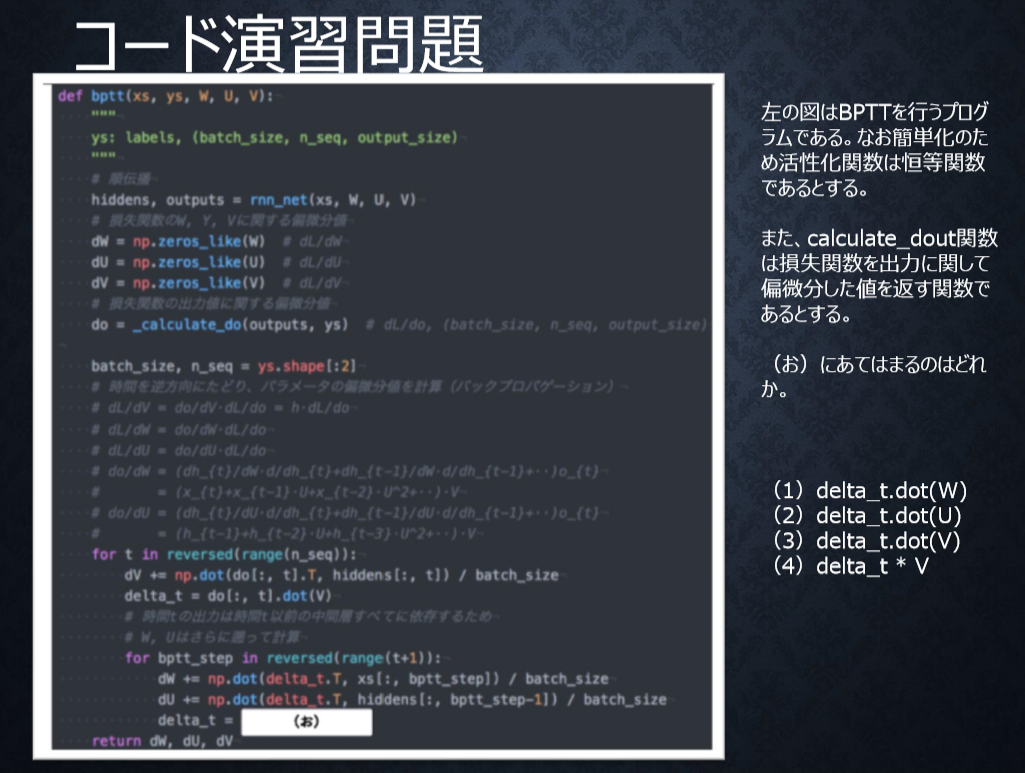
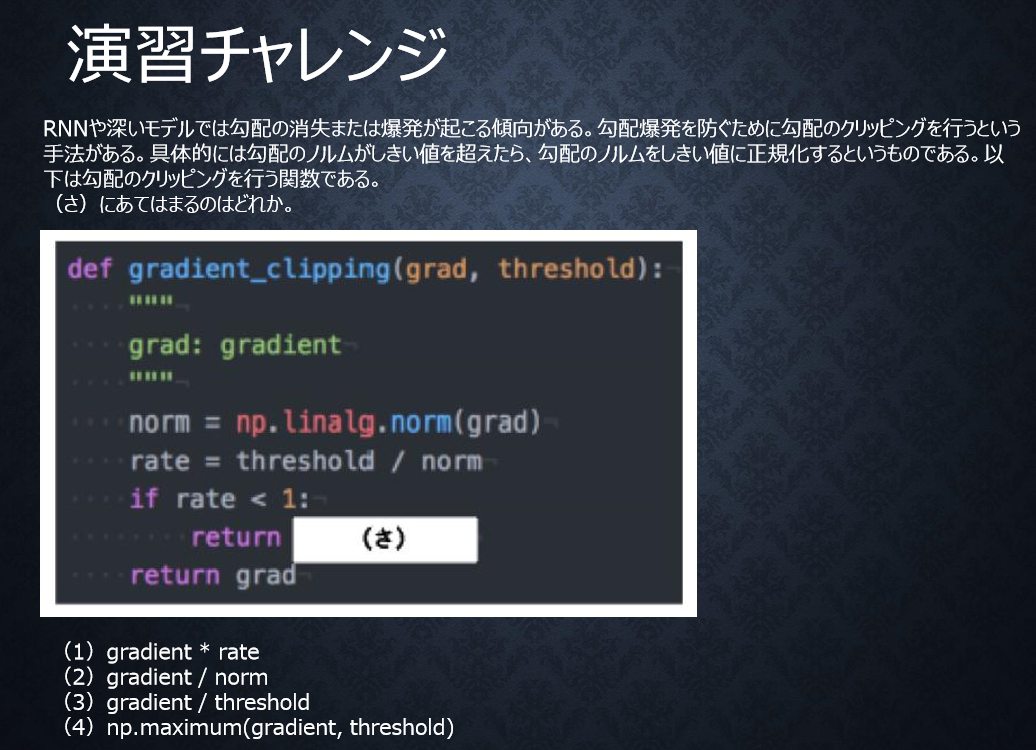
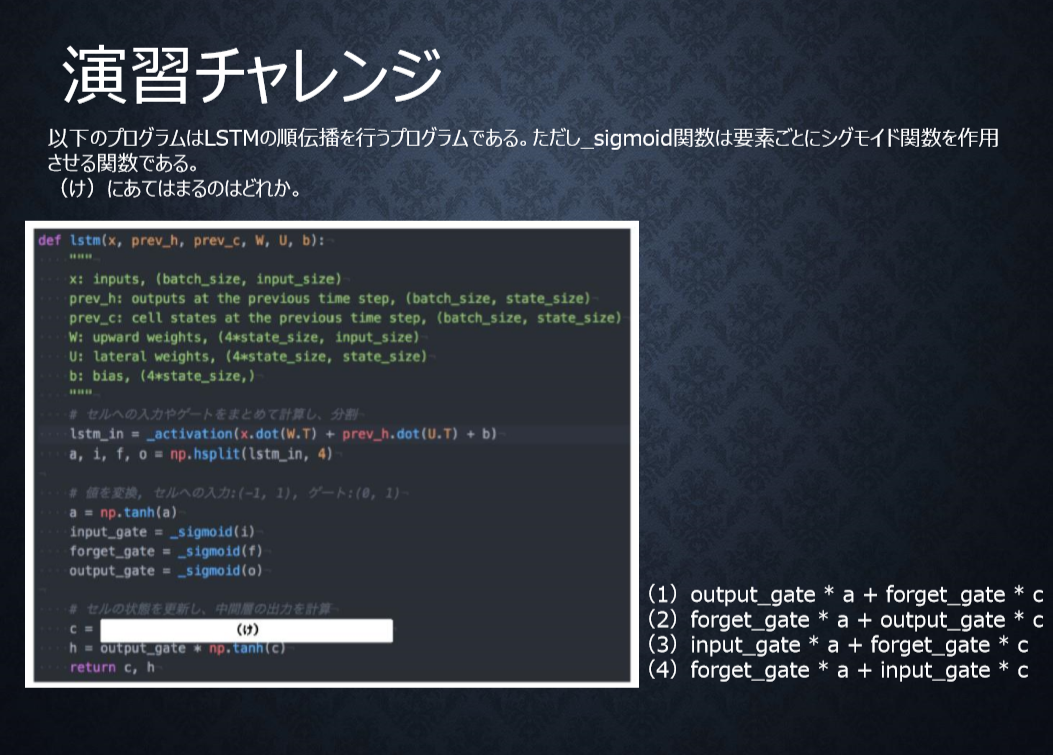
コード演習問題、演習チャレンジ

P26
bb.png

＜答え＞
２
隣接単語（表現ベクトル）から表現ベクトルを作るという処理は、隣接している表現leftとrightを合わせたものを特徴量としてそこに重みを掛けることで実現する。

P54
bbb.png

＜答え＞
２
過去に遡るたびにUが掛けられるため。

P66
bbbb.png

＜答え＞
１
勾配のノルムをしきい値に正規化するので、勾配×(しきい値/勾配のノルム)と計算される。

P80
bbbbb.png

＜答え＞
３
新しいセルの状態は、計算されたセルへの入力と1ステップ前のセルの状態に入力ゲート、忘却ゲートを掛けて足し合わせたものと表現される。

P91
bbbbbb.png

＜答え＞
４
新しい中間状態は、1ステップ前の中間表現と計算された中間表現の線形和で表現される。

P96
bbbbbbb.png

＜答え＞
４
双方向RNNでは、順方向と逆方向に伝播したときの中間層表現をあわせたものが特徴量となる。

P111
bbbbbbbb.png

＜答え＞
１
単語wはone-hotベクトルであり、それを単語埋め込みにより別の特徴量に変換する。

演習問題

3_1_simple_RNNを編集してRNNの挙動ついて理解する。

コードの一部


def d_tanh(x):
    return 1/(np.cosh(x) ** 2)

input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1

weight_init_std = 1
learning_rate = 0.1

iters_num = 10000
plot_interval = 100

# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)
# Xavier
# W_in = np.random.randn(input_layer_size, hidden_layer_size) / (np.sqrt(input_layer_size))
# W_out = np.random.randn(hidden_layer_size, output_layer_size) / (np.sqrt(hidden_layer_size))
# W = np.random.randn(hidden_layer_size, hidden_layer_size) / (np.sqrt(hidden_layer_size))
# He
# W_in = np.random.randn(input_layer_size, hidden_layer_size) / (np.sqrt(input_layer_size)) * np.sqrt(2)
# W_out = np.random.randn(hidden_layer_size, output_layer_size) / (np.sqrt(hidden_layer_size)) * np.sqrt(2)
# W = np.random.randn(hidden_layer_size, hidden_layer_size) / (np.sqrt(hidden_layer_size)) * np.sqrt(2)

for i in range(iters_num):

    # A, B初期化 (a + b = d)
    a_int = np.random.randint(largest_number/2)
    a_bin = binary[a_int] # binary encoding
    b_int = np.random.randint(largest_number/2)
    b_bin = binary[b_int] # binary encoding

    # 正解データ
    d_int = a_int + b_int
    d_bin = binary[d_int]

    # 出力バイナリ
    out_bin = np.zeros_like(d_bin)

    # 時系列全体の誤差
    all_loss = 0    

    # 時系列ループ
    for t in range(binary_dim):
        # 入力値
        X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1)
        # 時刻tにおける正解データ
        dd = np.array([d_bin[binary_dim - t - 1]])

        u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
        z[:,t+1] = functions.sigmoid(u[:,t+1])
#         z[:,t+1] = functions.relu(u[:,t+1])
#         z[:,t+1] = np.tanh(u[:,t+1])    
        y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))


        #誤差
        loss = functions.mean_squared_error(dd, y[:,t])

        delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_sigmoid(y[:,t])        

        all_loss += loss

        out_bin[binary_dim - t - 1] = np.round(y[:,t])


    for t in range(binary_dim)[::-1]:
        X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1)        

        delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_sigmoid(u[:,t+1])
#         delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_relu(u[:,t+1])
#         delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * d_tanh(u[:,t+1])    

        # 勾配更新
        W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
        W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))
        W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1))

    # 勾配適用
    W_in -= learning_rate * W_in_grad
    W_out -= learning_rate * W_out_grad
    W -= learning_rate * W_grad

    W_in_grad *= 0
    W_out_grad *= 0
    W_grad *= 0


    if(i % plot_interval == 0):
        all_losses.append(all_loss)        
        print("iters:" + str(i))
        print("Loss:" + str(all_loss))
        print("Pred:" + str(out_bin))
        print("True:" + str(d_bin))
        out_int = 0
        for index,x in enumerate(reversed(out_bin)):
            out_int += x * pow(2, index)
        print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
        print("------------")

lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.show()

＜パラメータ＞
weight_init_std = 1
learning_rate = 0.1
hidden_layer_size = 16
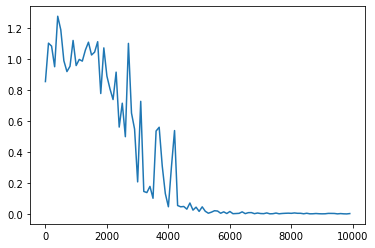
image.png
Loss:0.002512029789673937

weight_init_std を変更
＜パラメータ＞
weight_init_std = 10
learning_rate = 0.1
hidden_layer_size = 16
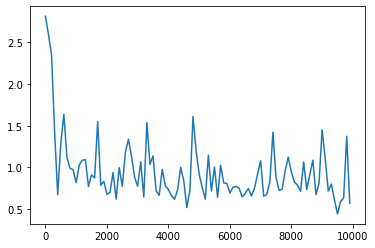
image.png
Loss:0.5695539219169825

learning_rate を変更
＜パラメータ＞
weight_init_std = 1
learning_rate = 0.3
hidden_layer_size = 16
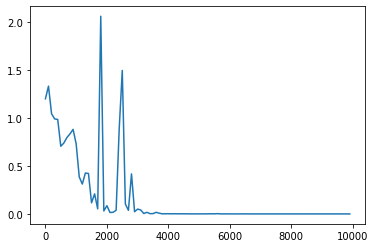
image.png
Loss:0.00010010663828942295

hidden_layer_size を変更
＜パラメータ＞
weight_init_std = 1
learning_rate = 0.1
hidden_layer_size = 160
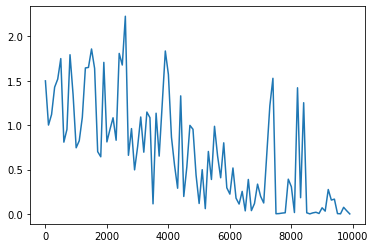
image.png
Loss:0.0007458298757409477

重みの初期化方法をXavierに変更
＜パラメータ＞
weight_init_std = 1
learning_rate = 0.1
hidden_layer_size = 16
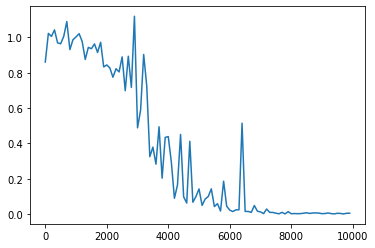
image.png
Loss:0.004681035449080068

重みの初期化方法をHeに変更
＜パラメータ＞
weight_init_std = 1
learning_rate = 0.1
hidden_layer_size = 16
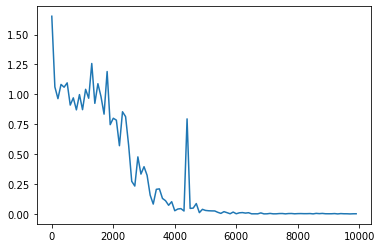
image.png
Loss:0.001741038048832916

活性化関数をsigmoidからReluに変更（重みの初期化方法はHe）
＜パラメータ＞
weight_init_std = 1
learning_rate = 0.1
hidden_layer_size = 16
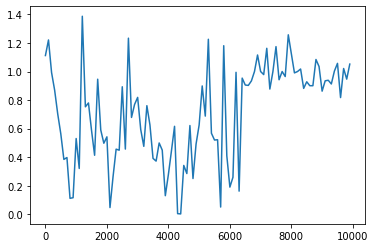
image.png
Loss:1.05211059838394

活性化関数をtanhに変更（重みの初期化方法はHe）
＜パラメータ＞
weight_init_std = 1
learning_rate = 0.1
hidden_layer_size = 16
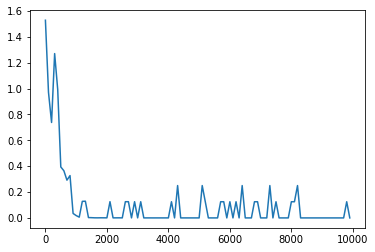
image.png
Loss:8.252632915272873e-06

活性化関数をtanhに変更（重みの初期化方法を元に戻した）
＜パラメータ＞
weight_init_std = 1
learning_rate = 0.1
hidden_layer_size = 16
image.png
Loss:0.12922737467134096

考察

  • ハイパーパラメータ、重みの初期値、活性化関数によって収束への挙動が変わることが分かった
  • RNNは通常のNNに比べて、中間層を次の入力にするため活性化関数や重みの選択が重要であることを理解した
  • 収束するためのパラメータ選択が非常に重要でかつ、難しいことを理解した
0
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
1