Datumix 遺伝的アルゴリズムで解くエイトクイーン問題
Datumixでは物流倉庫の自動化において、遺伝的アルゴリズム(Genetic Algorithms:GA)で最適化を行なっています。そこで我々の技術の一例として、今回は遺伝的アルゴリズムを用いたエイトクイーン問題(8-Queen問題)について取り上げたいと思います。
遺伝的アルゴリズムとは何か?
GAとは、1975年に発案された、生物の進化の法則を模倣して作られた解探索アルゴリズムです。GAを用いて解く有名な問題として、ナップサック問題や巡回セールスマン問題があげられます。全探索では計算量が大きすぎて到底計算できないような問題をGAを用いて解くことで、比較的短い時間で最適解に近づくことができます。
例えば、循環セールスマン問題において32箇所巡る箇所があるとし、組み合わせを全探索で求めようとするとスーパーコンピューターで百兆年以上かかりますが、GAだとそこまで時間をかけずにある程度最適な解を求めることができます。(参考1)
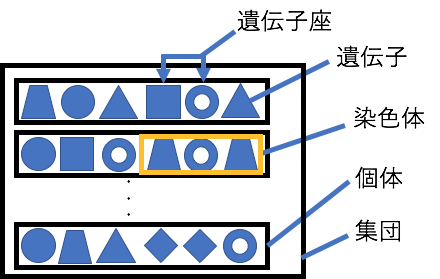
GAではデータを遺伝子として表現し、適応度がより良くなるような遺伝子の組み合わせ(個体)を探索します。その時、優位な個体を選択した後、遺伝子同士を交叉し、そして遺伝子の突然変異を起こすことで、より良い個体を次世代に残していきます。ある一定の適応度を満たした時、その遺伝子の組み合わせが「解」となります。
8-Queen問題とは?
8×8のチェス盤に8個のクイーンを互いに取られないように配置する問題です。
イメージ例:(参考2)
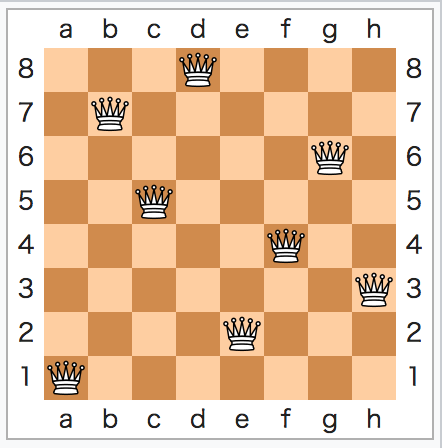
クイーンの位置は1行に1つしかクイーンを置けないことを前提にし、一次元ベクトルで表現しています。適応度は全てのクイーンが互いに取れる数とします。上の例だと、クイーンの位置を左から数えた[3,1,6,2,5,7,4,0]と表現でき、互いに全く取り合える位置にいないため適応度は0となります。8クイーン問題ではこのような全てのクイーンがお互いに取り合えない配置が最適解となります。
よって、この記事では適応度が低いほど「より良い個体」であり、適応度が0の個体を出力することを目的とします。
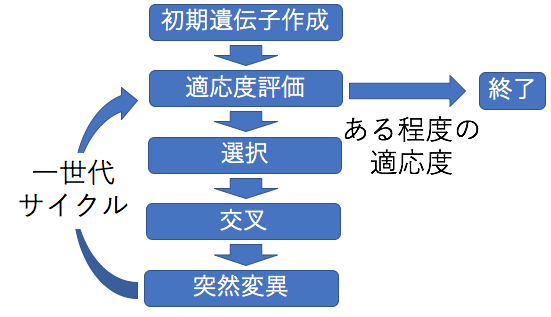
今回は、遺伝的アルゴリズムの各要素との対応関係は以下のようになっています。

では、実際に遺伝的アルゴリズムの流れの図に沿ってコードを書いていきます。
初期遺伝子作成
まず、初期遺伝子はgGeneCntで個体数を指定し、8×gGeneCnt分、0~7までのランダムな整数をリストに格納することで作ります。今回はgGeneCnt=50で試しています。
個体と適応度は[[3,1,6,2,5,7,4,0],0]のように格納しています。
def initialization():
gene_set_ = []
for i in range(gGeneCnt):
gene = []
queen_list = []
for j in range(8):
queen = int(np.random.rand()*8)
queen_list.append(queen)
gene.append(queen_list)
gene.append(calcFitness(gene[0]))
gene_set_.append(gene)
return gene_set_
各個体は以下のような関数でボード上に可視化します。
def arrangement(gene):
board = np.zeros((8,8), dtype=int)
for i, queen in enumerate(gene[0]):
board[i][queen] = 1
return board
# 表示結果
array([[0, 0, 0, 1, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 1, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0, 0]])
適応度
次に適応度を計算します。クイーンが互いに取り合える数を適応度としています。例えば、1組のみクイーンが互いに取り合える位置にいるとすると、適応度は2となります。適応度が0の個体を作成して遺伝子を出力することが目標です。
def evaluate(gene):
est = 0
board = arrangement(gene)
for i, queen in enumerate(gene):
q_x = queen
q_y = i
for j in range(8):
#縦にqueenがあるか?
if board[j][q_x] == 1 and j != q_y:
est += 1
#斜めにqueenがあるか?
vertical = i+j
horizontal = q_x + j
if vertical < 8 and horizontal < 8:
if board[vertical][horizontal] == 1 and j != 0:
est += 1
vertical = i-j
horizontal = q_x - j
if vertical > -1 and horizontal > -1:
if board[vertical][horizontal] == 1 and j != 0:
est += 1
vertical = i-j
horizontal = q_x + j
if vertical > -1 and horizontal < 8:
if board[vertical][horizontal] == 1 and j != 0:
est += 1
vertical = i+j
horizontal = q_x - j
if vertical < 8 and horizontal > -1:
if board[vertical][horizontal] == 1 and j != 0:
est += 1
return est
選択方法
次に選択方法です。今回は適応度が低いものほど選択されやすいルーレット選択を採用しました。適応度の逆数をとり、確率の違いを顕著にするため2乗しています。個体数の50個のうち、一つの個体が選ばれる確率は大体0%~20%で、選択されるのは毎回大体1つです。実行する時には選択を25回ほど繰り返して25個より良い個体を選んでいます。
def selection(gene_set_):
p = np.zeros(len(gene_set_))
next_gene_set_ = []
for i, gene in enumerate(gene_set_):
if gene[1] == 0:
est = 10000
else:
est = 1/(gene[1]**2)
p[i] = est
p = p/sum(p)
unique = np.random.rand(len(gene_set_))
for i in range(len(gene_set_)):
if p[i] > unique[i]:
next_gene_set_.append(gene_set_[i])
return next_gene_set_
交叉
次に交叉です。この交叉では、確率的に互換部分を決定する一点交叉を採用しています。
①現地点での個体の中からランダムに2つ個体を選択する
②50%の確率で1か4を選ぶ (この数値は変更可能)
③50%の確率で選んだ数字より以前か以降を選ぶ
例:4を選択し、以降を選んだ場合
[[0, 4, 7, 7, 2, 6, 6, 1], 6]
[[0, 6, 1, 5, 3, 7, 2, 6], 14]
⇩
[[0, 4, 7, 7, 2, 7, 2, 6], 8]
[[0, 6, 1, 5, 3, 6, 6, 1], 16]
④選ばれた染色体を交換して(交叉)できた計2つの遺伝子の中で、適応度が低い方を次の世代へ追加する
def cross_over(gene_a, gene_b):
next_gene_a = [[], 0]
next_gene_b = [[], 0]
next_gene_c = [[], 0]
next_gene_d = [[], 0]
temp_list = []
gene_point = 0
if random.randint(0,1) == 0:
gene_point = 1
else:
gene_point = 4
if random.randint(0,1) == 0:
next_queens_a = gene_a[0][:gene_point]
next_queens_a += gene_b[0][gene_point:]
next_queens_b = gene_b[0][:gene_point]
next_queens_b += list(gene_a[0][gene_point:])
next_gene_a[0] = next_queens_a
next_gene_b[0] = next_queens_b
next_gene_a[1] = calcFitness(next_gene_a[0])
next_gene_b[1] = calcFitness(next_gene_b[0])
temp_list.append(next_gene_a)
temp_list.append(next_gene_b)
else:
next_queens_a = gene_a[0][gene_point:]
next_queens_a += gene_b[0][:gene_point]
next_queens_b = gene_b[0][gene_point:]
next_queens_b += list(gene_a[0][:gene_point])
next_gene_c[0] = next_queens_a
next_gene_d[0] = next_queens_b
next_gene_c[1] = calcFitness(next_gene_c[0])
next_gene_d[1] = calcFitness(next_gene_d[0])
temp_list.append(next_gene_c)
temp_list.append(next_gene_d)
return temp_list
突然変異
ランダム値がたくさんありますが、
集団の中からどの個体を選ぶか
⇩
個体の中からどの遺伝子座を選ぶか
⇩
遺伝子をどんな値にするか
を決定するのにランダム値を用いています。
geneidx = random.randint(0,gGeneCnt-1)
posidx = random.randint(0,7)
valrand = random.randint(0,7)
gene_list[geneidx][0][posidx] = valrand
実行
最後に実行部分です。
gGeneCnt = 50
def myFunc(e):
return e[1]
# 初期遺伝子を作成
gene_list = initialization()
loop = 0
while True :
loop += 1
idx = 0
# 突然変異
for i in range(gGeneCnt//2):
geneidx = random.randint(0, gGeneCnt-1)
posidx = random.randint(0, 7)
valrand = random.randint(0, 7)
gene_list[geneidx][0][posidx] = valrand
# 適応度リセット
for i, gene in enumerate(gene_list):
gene_list[i][1] = calcFitness(gene[0])
# 選択:ルーレット選択で約半分を抽出
temp_gene_list = []
for i in range(gGeneCnt//2):
temp = selection(gene_list)
if temp == []:
continue
else:
for j in temp:
temp_gene_list.append(j)
if temp_gene_list == []:
temp_gene_list = copy.deepcopy(gene_list)
# 選択したものの中からランダムに2つ選んで交叉
next_gene_list = []
while(len(next_gene_list) < len(gene_list)):
after_cross_over = []
r_a, r_b = np.random.choice(range(len(temp_gene_list)), 2)
r_gene_a, r_gene_b = temp_gene_list[r_a], temp_gene_list[r_b]
after_cross_over = cross_over(r_gene_a, r_gene_b)
next_gene_list.append(min(after_cross_over, key=myFunc))
# 現世代の中で最も適応度が低い個体を表示
min_fitness = min(next_gene_list, key=myFunc)
print(loop, 'th generation, minimum fitness is: ', min_fitness)
# その個体の適応度が0になった時、それが解
if min_fitness[1] <= 0:
print("Loop end = " + str(loop) + ", Fitness = " + str(min_fitness))
print(arrangement(min_fitness))
break
gene_list = copy.deepcopy(next_gene_list)
結果と検証
実行すると、以下のような結果が出て来ます。各世代で適応度が最も低い個体を出力し、最適解が見つかったときに世代サイクル数と最適解をボードで表現しています。
1 th generation, minimum fitness is: [[7, 1, 4, 7, 5, 3, 6, 6], 6]
2 th generation, minimum fitness is: [[7, 4, 0, 5, 0, 2, 6, 1], 6]
3 th generation, minimum fitness is: [[3, 6, 6, 4, 1, 7, 0, 2], 4]
4 th generation, minimum fitness is: [[3, 1, 6, 4, 1, 7, 0, 2], 2]
5 th generation, minimum fitness is: [[4, 7, 3, 0, 2, 5, 1, 6], 0]
Loop end = 5, Fitness = [[4, 7, 3, 0, 2, 5, 1, 6], 0]
[[0 0 0 0 1 0 0 0]
[0 0 0 0 0 0 0 1]
[0 0 0 1 0 0 0 0]
[1 0 0 0 0 0 0 0]
[0 0 1 0 0 0 0 0]
[0 0 0 0 0 1 0 0]
[0 1 0 0 0 0 0 0]
[0 0 0 0 0 0 1 0]]
今回は5世代で終了していますが、40世代サイクル前後で最適解が見つかり、約1秒かかります。個体数のgGeneCntの数や突然変異の割合を増減させたり、選択部分のgene_pointを変えて検証したところ、今の所、紹介したような値が短時間で最適解を導き出しています。
注意事項として、交叉部分で交叉した後の2つの個体のうちより良い方を次世代に加えているので、交叉の後ある意味エリート選択をしていることになります。よって、このコードの全体の流れとしては以下のようになります。
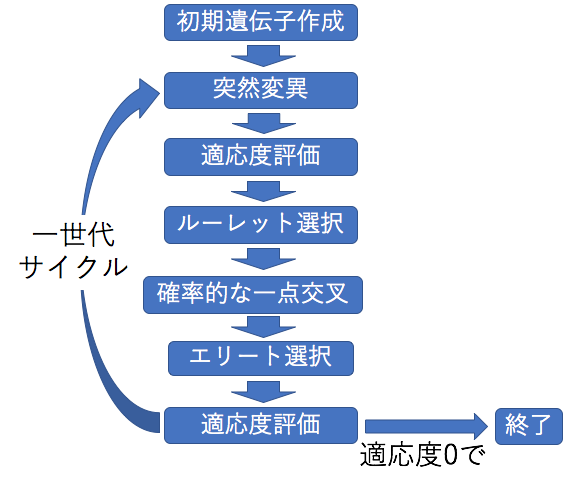
なお、ご紹介したコードが最適解を求めるのに最速であるとは限りません。交叉方法を変えたり、各パラメータを正しい方に変更すると処理時間が短くなるかもしれません。
考察
8-Queen問題でGAを使うにあたり、より重要な因子として、選択方法と交叉方法が挙げられますが、遺伝子の数や評価方法が違えば重要な因子は変わってくるかもしれません。交叉方法の中だけでも2点交叉、一様交叉、多点交叉などいくつもあり、それぞれに合った遺伝子数や選択方法は変わってきます。8-Queenでない問題では違った組み合わせが最適になるでしょう。