気軽にフーリエ解析したい

背景

交流を使った実験をしていると，測定系の補正とか入力と出力の相関を見るとか，周波数解析をしたいという場面が少なくありません。だいたいの時系列測定データはCSVファイルで得られるので，自前で解析する場合にはExcelのデータ分析ツールにあるFFTが取っ付きやすく便利です。
しかし，「対象データ数が2の冪乗個に制限される」ことや「出力が複素数なので後処理が面倒」といった問題があります。特に一つ目が致命的で，条件によってはせっかく取ったデータの大半がボツになる上に解析分解能が悲しいことになります。

そこで，データ制限を受けずにもっと手軽にフーリエ解析できればと思いPythonで実装してみました。

やりたかったこと

• CSV入力とCSV出力
• 簡単なGUI
• 周波数解析
• 特定の周波数または信号強度を閾値とするノイズ処理

実装

コード

dft_solver.py

import tkinter
import tkinter.filedialog as tkdialog
import os.path
import numpy as np
import matplotlib.pyplot as plt


# 解析とスムージング選択用GUI
def interface_top():
    root = tkinter.Tk()

    def bfunc1():
        global switch
        switch = 0
        root.destroy()

    def bfunc2():
        global switch
        switch = 1
        root.destroy()

    b1 = tkinter.Button(text='周波数解析', command=bfunc1)
    b1.grid(column=0, row=0)
    b2 = tkinter.Button(text='ノイズ処理', comman=bfunc2)
    b2.grid(column=0, row=1)

    root.mainloop()


# 周波数解析用GUI
def interface_analyze():
    root = tkinter.Tk()
    ftyp = [('CSVファイル', '*.csv')]
    idir = '/home/ユーザ名/'

    def bfunc1():
        global fpath, fname
        fpath = tkdialog.askopenfilename(filetypes=ftyp, initialdir=idir)
        fname, ext = os.path.splitext(os.path.basename(fpath))

    def bfunc2():
        global meas_unit
        meas_unit = float(e1.get())
        root.destroy()

    l1 = tkinter.Label(root, text='データの測定間隔(sec)')
    l1.grid(column=0, row=0)
    e1 = tkinter.Entry(root, bd=1)
    e1.grid(column=1, row=0)
    l3 = tkinter.Label(root, text='入力csvファイル')
    l3.grid(column=0, row=2)
    b1 = tkinter.Button(text='choose', command=bfunc1)
    b1.grid(column=1, row=2)
    b2 = tkinter.Button(text='analyze', comman=bfunc2)
    b2.grid(column=2, row=3)

    root.mainloop()


# スムージング処理用GUI
def interface_noise():
    root = tkinter.Tk()
    ftyp = [('CSVファイル', '*.csv')]
    idir = '/home/ユーザ名/'

    def bfunc1():
        global fpath, fname
        fpath = tkdialog.askopenfilename(filetypes=ftyp, initialdir=idir)
        fname, ext = os.path.splitext(os.path.basename(fpath))

    def bfunc2():
        global meas_unit, cutoff_fq_low, cutoff_fq_high, cutoff_amp
        meas_unit = float(e1.get())
        cutoff_fq_low = float(e2.get())
        cutoff_fq_high = float(e4.get())
        cutoff_amp = float(e3.get())
        root.destroy()

    l1 = tkinter.Label(root, text='データの測定間隔(sec)')
    l1.grid(column=0, row=0)
    e1 = tkinter.Entry(root, bd=1)
    e1.grid(column=1, row=0)
    l2 = tkinter.Label(root, text='カットオフ周波数(Hz)')
    l2.grid(column=0, row=1)
    e2 = tkinter.Entry(root, bd=1)
    e2.grid(column=1, row=1)
    l5 = tkinter.Label(root, text='から')
    l5.grid(column=2, row=1)
    e4 = tkinter.Entry(root, bd=1)
    e4.grid(column=3, row=1)
    l3 = tkinter.Label(root, text='カットオフ振幅強度')
    l3.grid(column=0, row=2)
    e3 = tkinter.Entry(root, bd=1)
    e3.grid(column=1, row=2)
    l4 = tkinter.Label(root, text='入力csvファイル')
    l4.grid(column=0, row=3)
    b1 = tkinter.Button(text='choose', command=bfunc1)
    b1.grid(column=1, row=3)
    b2 = tkinter.Button(text='filtering', comman=bfunc2)
    b2.grid(column=4, row=4)

    root.mainloop()


# 離散フーリエ変換
def fourier_analysis(in_signal, interval):
    signal = np.genfromtxt(in_signal, delimiter=',')
    dnumber = signal.shape[0]
    yaxis = signal[:, 1]
    f_signal = np.fft.fft(yaxis)
    fq = np.linspace(0, 1.0 / interval, dnumber)

    if switch == 0:
        f_abs = np.abs(f_signal)
        f_abs_amp = f_abs / dnumber * 2
        f_abs_amp[0] = f_abs_amp[0] / 2  # 直流成分のみ2で割る

        # 測定間隔によって周波数単位を変更
        if interval < 1e-9:
            fq = fq * 1e-9
        elif 1e-9 <= interval < 1e-6:
            fq = fq * 1e-6
        elif 1e-6 <= interval < 1e-3:
            fq = fq * 1e-3
        elif 1e-3 <= interval:
            fq = fq * 1

        data = np.c_[fq[:int(dnumber / 2) + 1], f_abs_amp[:int(dnumber / 2) + 1]]
        return data

    if switch == 1:
        nyq_cutoff_fq_low = (1.0 / interval) - cutoff_fq_low    # ナイキスト周波数に関して対称な周波数
        nyq_cutoff_fq_high = (1.0 / interval) - cutoff_fq_high
        f_abs = np.abs(f_signal)
        f_abs_amp = f_abs / dnumber * 2
        f_signal[((cutoff_fq_low <= fq) & (cutoff_fq_high > fq))] = 0  # カットオフ周波数未満の信号を0に
        f_signal[((nyq_cutoff_fq_high < fq) & (nyq_cutoff_fq_low >= fq))] = 0
        f_signal[(f_abs_amp < cutoff_amp)] = 0  # カットオフ振幅未満の信号を0に
        inv_signal = np.fft.ifft(f_signal)
        inv_signal_real = inv_signal.real
        dlabel = np.arange(dnumber)
        data = np.c_[dlabel, inv_signal_real]
        return data


# 周波数解析用データ書き込み
def write_result_dft(analyzed_data, interval):
    global label
    result = analyzed_data.tolist()

    # csvのラベル部分の処理
    if interval < 1e-9:
        label = ['Frequency(GHz)', 'Amplitude']
        result.insert(0, label)
    elif 1e-9 <= interval < 1e-6:
        label = ['Frequency(MHz)', 'Amplitude']
        result.insert(0, label)
    elif 1e-6 <= interval < 1e-3:
        label = ['Frequency(kHz)', 'Amplitude']
        result.insert(0, label)
    elif 1e-3 <= interval:
        label = ['Frequency(Hz)', 'Amplitude']
        result.insert(0, label)

    np.savetxt(os.path.dirname(fpath) + '/' + fname + '_DFT_analyzed.csv', result, delimiter=',', fmt='%s')


# スムージング処理用データ書き込み
def write_result_idft(analyzed_data):
    result = analyzed_data.tolist()
    np.savetxt(os.path.dirname(fpath) + '/' + fname + '_smoothed.csv', result, delimiter=',', fmt='%s')


# グラフ作成
def plot_graph(analyzed_data):
    plt.rcParams['font.size'] = 22
    plt.rcParams['font.family'] = 'Times New Roman'
    xaxis = analyzed_data[:, 0]
    yaxis = analyzed_data[:, 1]
    plt.subplot(1, 1, 1)
    plt.plot(xaxis, yaxis, '.-')
    if switch == 0:
        plt.xlabel(str(label[0]))
        plt.ylabel('Amplitude')
    elif switch == 1:
        plt.xlabel('Time')
        plt.ylabel('Signal')
    plt.show()


# メイン処理
def mainfunc():
    interface_top()

    if switch == 0:
        interface_analyze()
        spectrum = fourier_analysis(fpath, meas_unit)
        write_result_dft(spectrum, meas_unit)
        plot_graph(spectrum)

    elif switch == 1:
        interface_noise()
        spectrum = fourier_analysis(fpath, meas_unit)
        write_result_idft(spectrum)
        plot_graph(spectrum)


if __name__ == '__main__':
    mainfunc()

#テスト
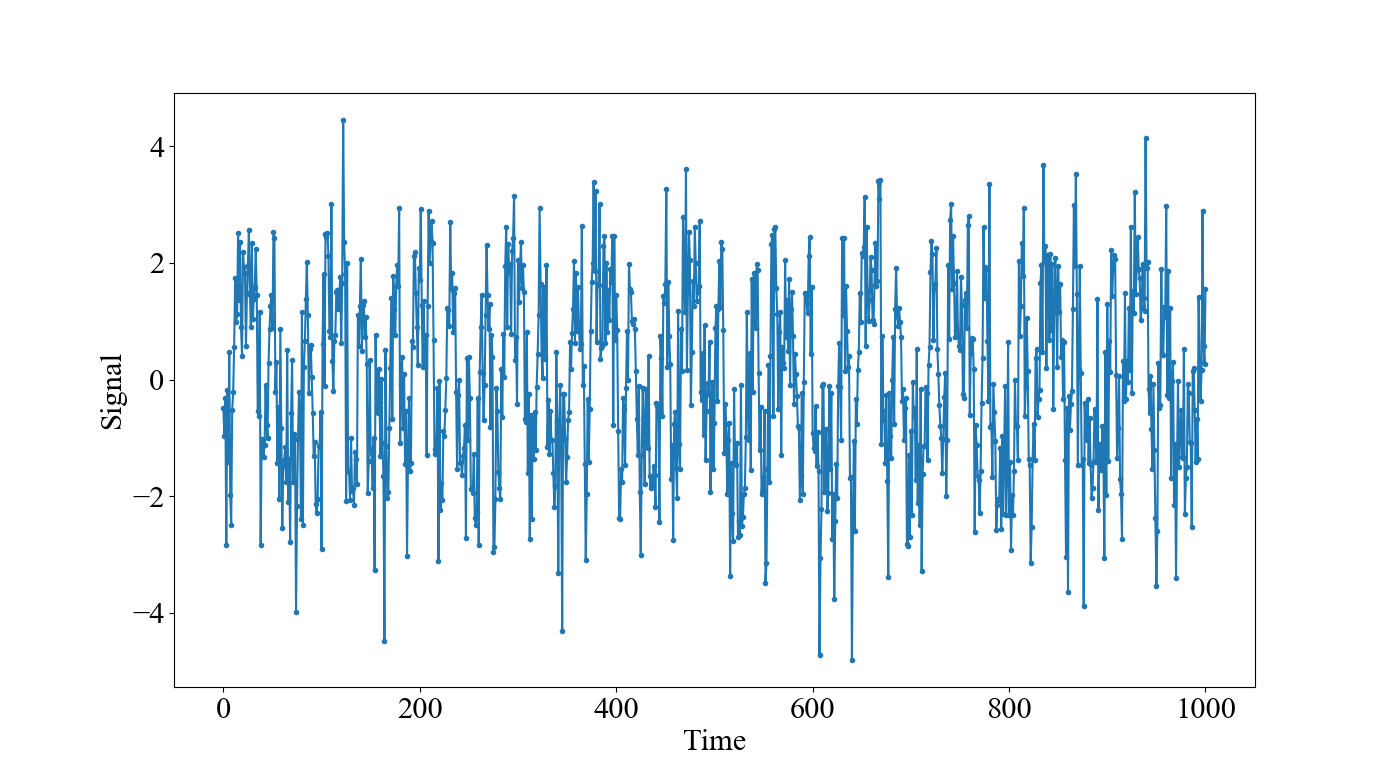
測定間隔が1 msで1001 個のデータが取得できる系を想定し，11 Hz，33 Hz，55 Hzの正弦波を同強度で足し合わせてノイズを乗せた次のような信号をテストデータとして用います。

original.csv

0,-0.48397133
1,-0.967047196
2,-0.309136861
    ・・・
999,0.263109874
1000,1.558069472

ぐっちゃぐちゃですね。とりあえず周波数解析してみます。

original_DFT_analyzed.csv

11.0,0.9852335962080552
        ・・・
33.0,1.0266188812665253
        ・・・
55.0,1.012834430978335

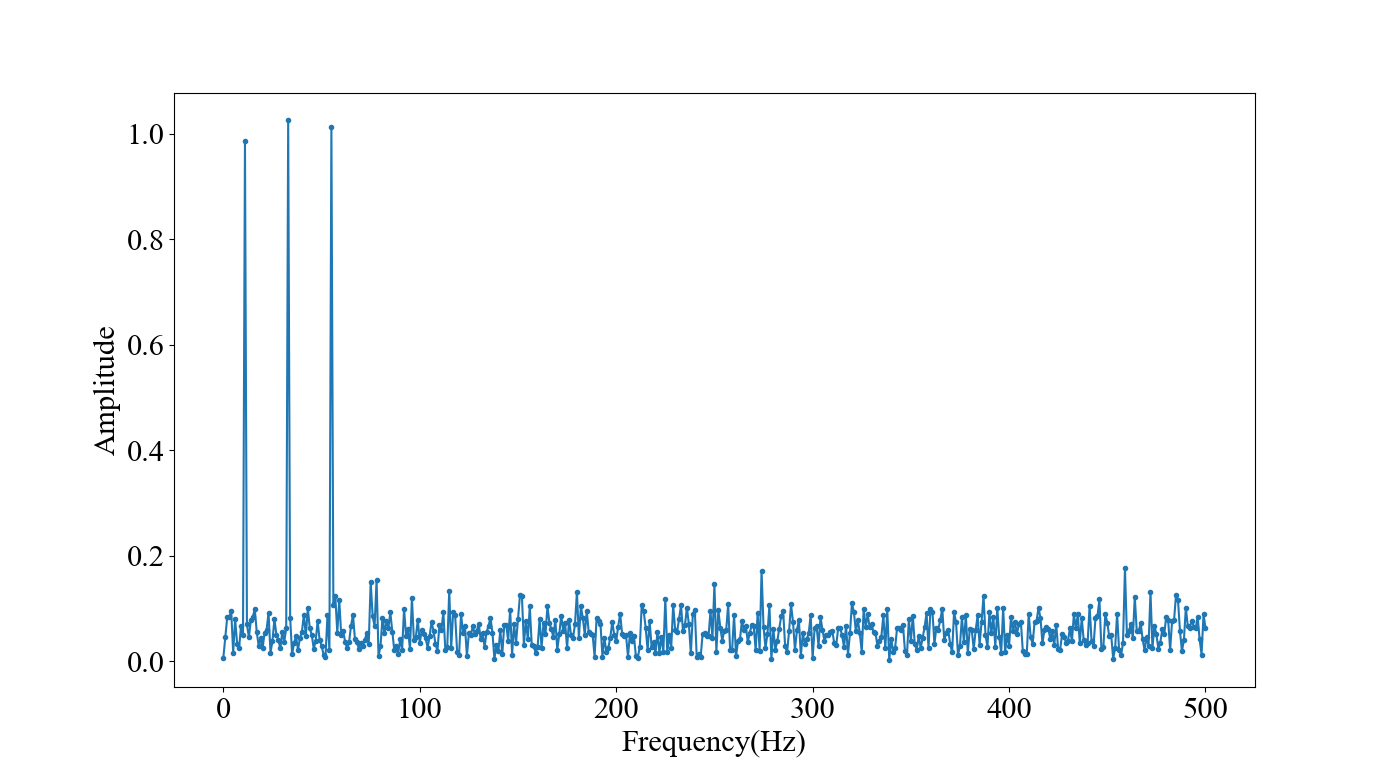
各成分で強度差が認められますが，綺麗に分離できてる感じはします。ので，次に，強度0.5未満の成分を間引いて逆フーリエすることで元の信号からノイズ成分を除去してみます。


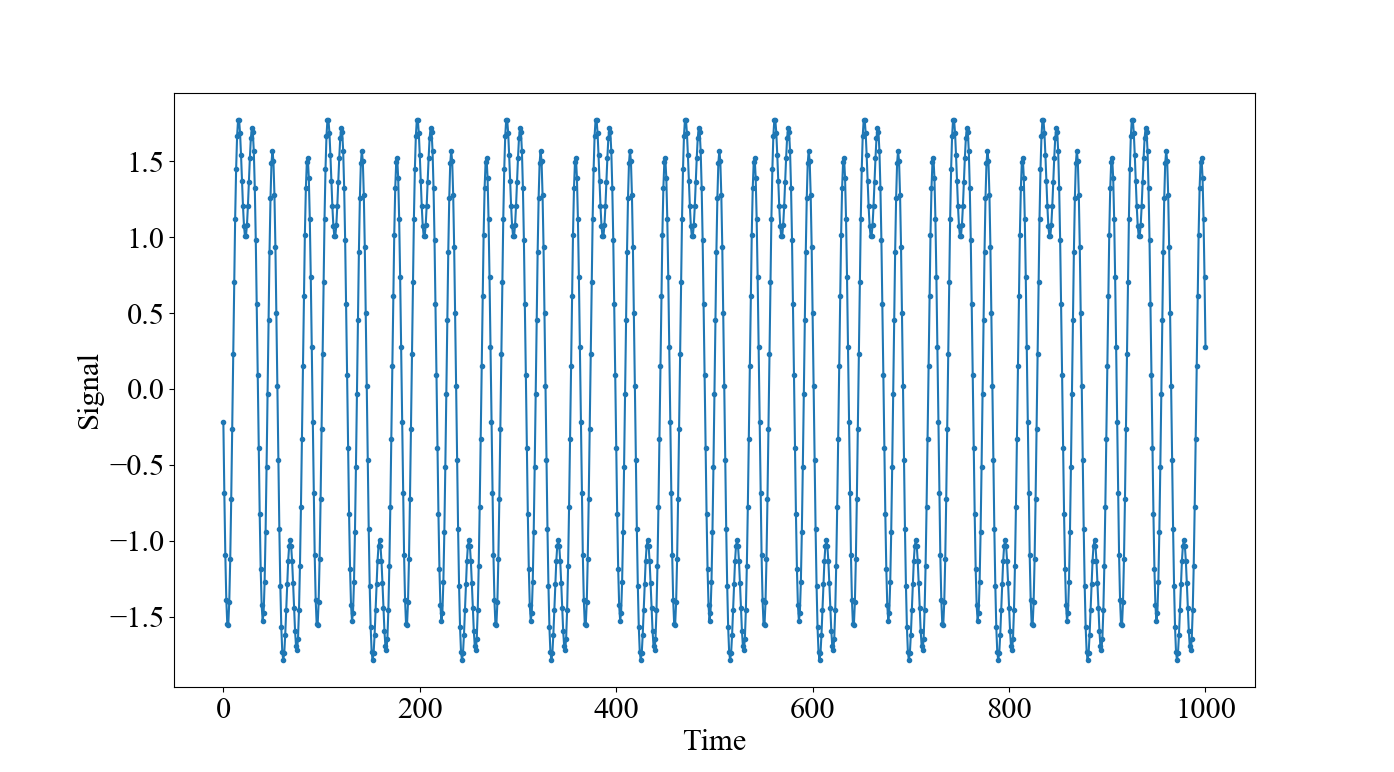
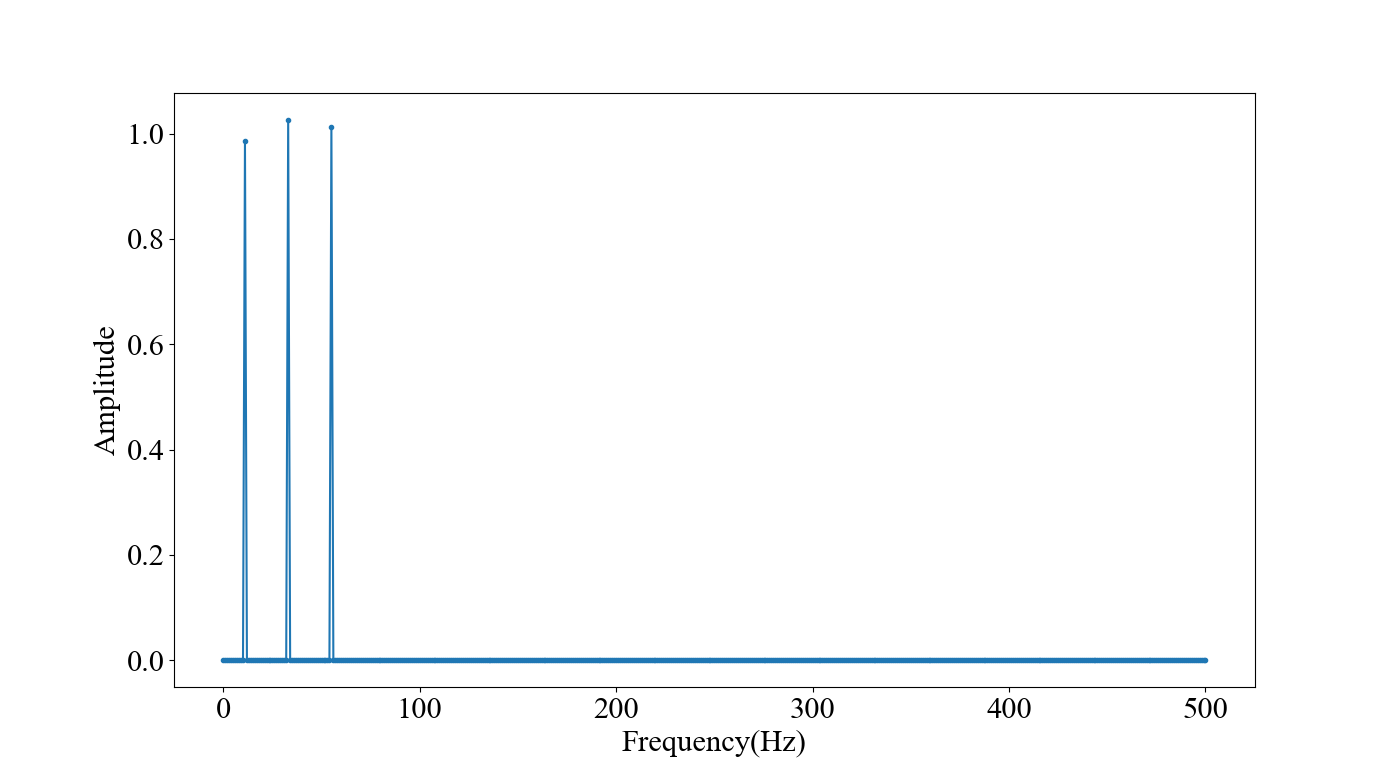
それっぽい波形になりました。
ここで，「55 Hz付近の成分も消したいな」となったとします。スペクトルを見てみると強度で除外するのは面倒そうなので，素直に周波数で間引いてあげます。


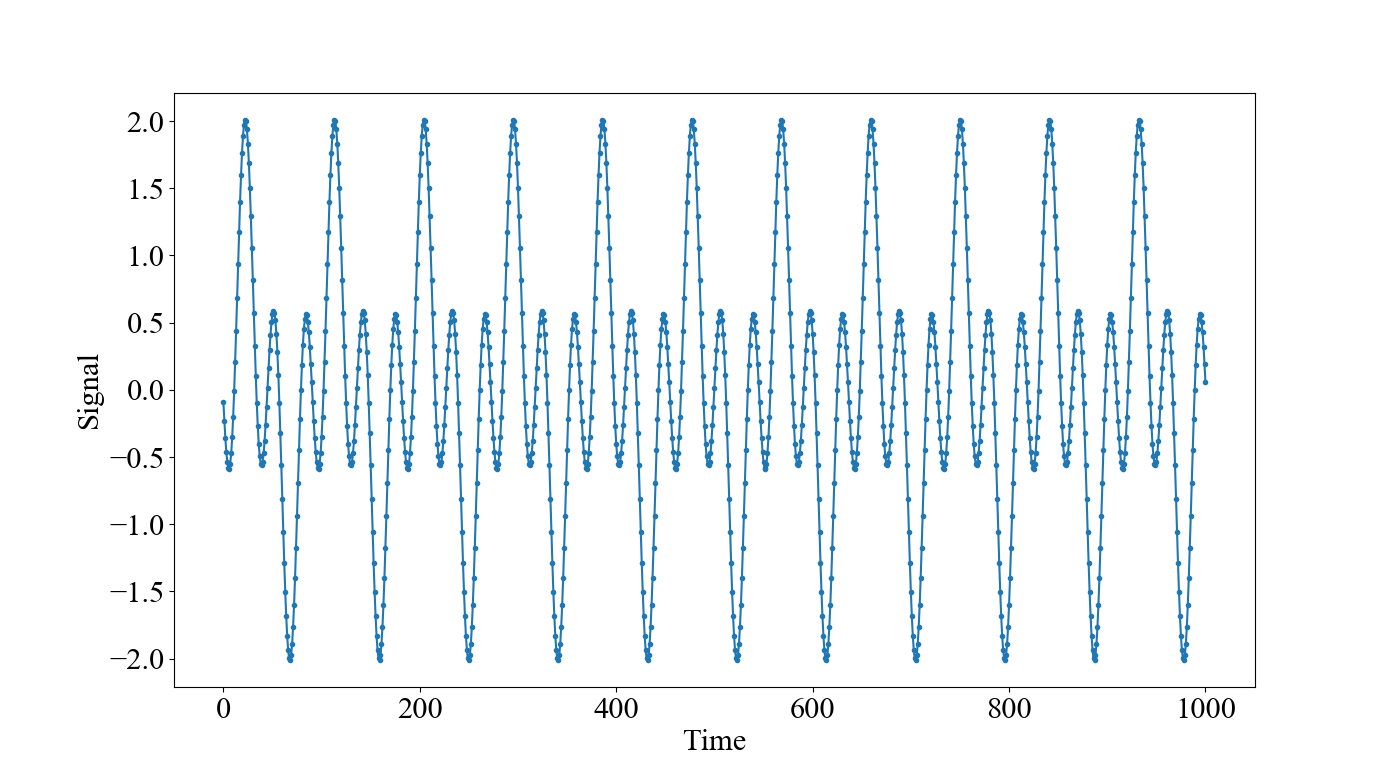
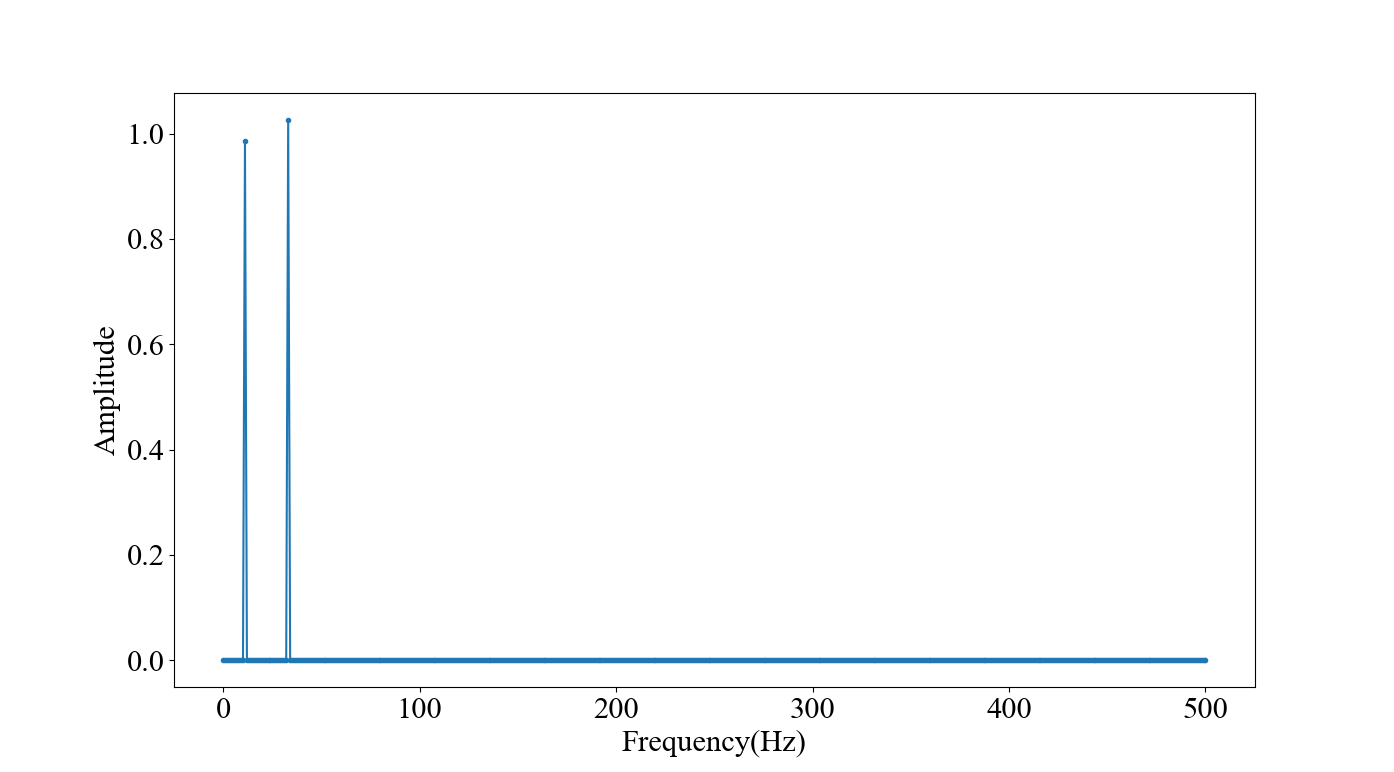
こちらも問題なく処理できていそうです。

まとめ

以上，気軽にフーリエ解析できました。
特に目新しいことはやっていませんが，同じような境遇の方の一助になれば幸いです。