目次
1. はじめに
鈴鹿高専のプロコンでは電子回路やフロントエンド、バックエンド、セキュリティ、機械学習など、数多くの分野が扱われています。なればこそ、今こそ量子コンピュータにも手を出してみよう!というのがこの記事の目的です(というのは建前で、書ける内容が無かったので皆さんが書いてなさそうなやつを選びました)。量子コンピュータに興味を持ってもらうことが目的のため、数学・物理学的な厳密性はほぼなく (というか自分が理解できていない)、量子コンピューティングに欠かせない数式や回路図も登場しません。直感的な話になるように解釈している節があるので、もし間違い等あれば指摘していただけると幸いです。
(余談ですが、最近授業で現行PCの誤り訂正の話がされていて、すごくタイムリーな記事になりました。同学年の人がこの記事を見てくれていることを祈ります...)
2. なぜ誤り訂正なのか
みなさんが量子コンピュータと聞くと、いつも使ってるPCと何が違うのかとか、素因数分解のアルゴリズムはどうなっているのだとかの方が気になると思います。ではなぜ誤り訂正の話をするのか、それはこの技術が量子コンピュータの実現に大きく関わっており、同分野の中でもホットな研究テーマだからです。
量子コンピュータのアルゴリズムはいろいろありますが、その多くは物理ビットに対して誤り訂正がされた論理ビットを使うことを想定しており、現在実現している量子コンピュータはこの内物理ビットを使用しています。では残りのアルゴリズムは何なのかというと、それはNISQ(Noisy Intermediate-Scale Quantum device)で使用することを想定したものです。このNISQはまさに先ほど言った「現在実現している量子コンピュータ」であり、NISQで用いられるアルゴリズムはノイズがあっても古典コンピュータより効率的に動作することを目的に作られたものです。しかしビットの数が増えるほど誤り率は増加するので、量子コンピュータの性能を引き出すためにも、大規模な量子コンピュータ実現のためにも誤り訂正が必須なのです。
- ここでの量子コンピュータとは下の画像の赤線から右のものを指すとします
- 2018年の画像なので今とは状況が異なっています
- ピンクの部分は使用されている媒体で、量子コンピュータは様々な媒体を用いて実現が模索されています
(大阪大学 藤井研究室 「理論物理学特論Ⅱ2018 第1回:ガイダンス、量子力学の復習」のイントロ(pdf) p23より引用)
3. 古典誤り訂正との違い
量子コンピュータと古典コンピュータの違いは何か?といえば、最も分かりやすいのはアナログとデジタルの違いだと思います(これをアナログと呼んでいいのかは議論の余地があります)。量子コンピュータは量子力学の「重ね合わせ」という現象を利用しており、「0」の状態と「1」の状態が重ね合わさっているので、ビットの値は観測するまで0か1か決まりません(初期値として0である確率が100%なんてこともありますが)。それぞれのビットになる確率が量子ビットの持っている情報であり、1ビットであれば「0」になる確率と「1」になる確率が合計で1になっています。仮にn個の量子ビットがあったとすると、0と1の順列(01101...)の2^n個のパターンが重ね合わさっており、それぞれのパターンになる確率が合計で1になっています。2ビットだと00,01,10,11の4パターンで、観測される確率が等しいならそれぞれ25%ですね。この重ね合わせに正解のパターンの確立を上げる演算をすることで、複数の可能性を同時に考慮する並列処理が出来るわけです(パラレルワールドみたいでいいですね)。そしてこの重ね合わせの状態を維持することが、量子誤り訂正の目的です。しかしこの重ね合わせの状態は非常に不安定で、さらに次の古典ビットとの違いが、この量子誤り訂正をより難しくさせています。
- 誤りが連続であること
- ビットがコピー不可であること
- 訂正対象ビットの中身を確認できないこと
1. 誤りが連続であること
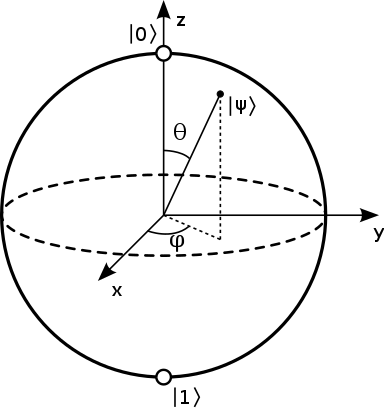
先程、量子ビットが持っている情報は連続だと述べました。ゆえに、誤りも連続になっています。...とはいえそれだけだとイメージしづらいと思うので、もう少し量子ビットについて説明します。最初に数式を出さないと宣言してしまったので具体的なことは言えないのですが、量子ビットの状態はブロッホ球という球の球面上の点として表すことが出来ます。
wikipedia(ブロッホ球)より引用
わかりやすい量子エラーだと、「X軸反転」に対応した「符号反転(ビットフリップ)」と、「Z軸反転」に対応した「位相反転(フェーズフリップ)」があります。
Y軸回転についてはX軸回転とZ軸回転で表せるので、この2つの回転で球の上を縦横無尽に誤ることが出来るわけです(?)。
ここで、量子コンピュータについてもっと勉強したい方向けに、いくつかサイトを貼っておきます
これらのサイトでは体系だった学習が出来る上、シミュレーター等を用いて挙動を確認しながら勉強ができます。
とはいえこれらのサイトは表現が難しかったりするので、視覚的に分かりやすい説明を付与してくださっている@shnchrさんの記事をお勧めします。今回の範囲だと、少しだけ予備知識があったので「パウリゲート(XYZ)を細かく見てみる」→「ブロッホ球と各種ゲートの関係」→「量子誤り訂正(shor's Code)」→「量子誤り訂正(Stabilizer Code)」の順で読みました。(さしずめこの記事は去年のアドベントカレンダーの雑まとめ...)
あと、定義的な部分をしっかりやるなら、大阪大学 藤井研究室の動画も今回の範囲を包括しているのでお勧めです。ただし、量子力学の話ががっつり出てくるので、ヨビノリさん等で量子力学に触れておくのをお勧めします。(範囲はだいたい微積分と偏微分、微分方程式、行列、複素数ですが、機械学習の時と違って行列の問題(固有値等)が結構入ってくるので、ロピタルの定理と同じ対象年齢説があります。でも動画内で適宜説明があるので、ヨビノリさんの動画までなら微積分ができれば多分行けます。)
追記 : ここにしっかり学ぶ人向けのカオスマップが書かれていました(https://www.qmedia.jp/qnative-education-chaosmap/)
ビットがコピー不可であること
量子複製不能定理により、量子情報はコピーすることが出来ません。古典ビットの誤り訂正では多数決を使った方法を最初の頃に習うと思うのですが、この制約により量子ビットでは使えません;;
訂正対象ビットの中身を確認できないこと
上の方で述べた通り、量子ビットは中身を確認した瞬間に1か0かが決定して重ね合わせの状態が崩れてしまうので、重ね合わせにより情報を送信する量子ビットでは、中身の確認は送信したい情報を破壊してしまうことに相当します。そのため、訂正対象のビットの状態を直接確かめることなく、元の状態に戻す必要があるのです。
本当に誤り訂正出来るのか?といったレベルですが、これから紹介する方法を使えば、エラーが連続だろうと元の状態が分からないだろうと、誤り訂正が出来てしまいます。
4. エラーの離散化
これは全ての量子誤り訂正に関わる話なので、先に書いておきます。なんと連続な量子エラーは離散的なエラーに収束し、X軸反転とZ軸反転に対応するだけで、任意のエラーも訂正できてしまうのです。これにより、「エラーが連続であること」の問題が解決します。
5. shorの符号
shorの符号は簡単に言うと、X軸反転とZ軸反転に個別に対応した回路を組み合わせたものです。では、どうやってこの2つの反転に対応するのでしょうか。ここで「重ね合わせ」に次ぐ2つ目の量子コンピュータの特徴、「量子もつれ」が登場します。
量子もつれは端的に言うと、「ある複数の量子がもつれあっている時、1つ量子の状態を観測すると、他の量子の状態も決定する」というものです。量子ビットを例にすると、「ある量子ビットを観測して0だった時、もつれ状態にあるビットも0か1か決まる」のが量子もつれです。では、どうやってこの量子もつれ状態を作るのかというと、量子コンピュータではCNOT(Controlled NOT)と呼ばれるゲートを用います。CNOTは簡単に言うとif文が付いたNOT演算で、制御ビットが1の時にターゲットビットに対してNOT演算を行います。もうお気づきの方もいると思いますが、0もしくは1で初期化しておいたターゲットビットをゲートに通した後に測定すると、制御ビットが0か1かが分かるのです。これはまさに量子もつれの挙動であり、そしてこれの奇妙な点は、観測するまでは全くランダムであったのに、どれだけの距離が離れていようともゼロ時間でその関係が成立することです(1万光年離せば1万年時間を遡行したともとれるので、タイムマシンじみた話ですね)。これを用いると古典ビットのようなコピーを行わなくても、|0⟩ビットや|1⟩ビットを|000⟩や|111⟩のように冗長化することができます。これで2つ目の問題、「ビットがコピー不可であること」が解決しました。
さて、残りの問題は「訂正対象ビットの中身を確認できないこと」ですが、これはエラーの離散化によってほぼ解決していると言えます。この問題の難しい点は「エラーが連続なため、どの状態に戻せばいいのか分からない」ことだったため、X,Z軸反転のみとわかった今、どの反転が起こったかを特定すれば、元の状態を復元できるわけです。
ここからは量子的な話をするとまだ色々あるのですが、直感的には古典誤り訂正と同じことをしています。つまりは、量子ビットの取りうる状態と補助ビット(冗長化に使用した、|000⟩ の|0"00"⟩の部分)の読み取り値を、1対1で対応させるのです。補助ビットは2ビットなので4つの値を取り、これが「|000⟩のそれぞれのビットが誤っている場合(3パターン) + 誤りが無い場合(1パターン)」に対応しているわけです。そして例のごとく、補助ビット2つだけだと1ビットの誤りまでしか対応できません。
この仕組みでX軸反転を訂正する回路、Z軸反転を訂正する回路を作成でき、この2つを組み合わせることでエラーの離散化により任意のエラーについても訂正できるわけです。
6. おわりに
いかがでしたでしょうか
今回は量子ビットの面白い|+⟩や|-⟩などの状態の話もすっ飛ばし、ほぼ古典ビットのような扱いで紹介をしました。実は最後の方に|0⟩と記したように、量子ビットは古典ビットとは全く違った性質を持っていて、演算なんかも、予想もできないような変化がたくさんあります。これを期に、量子力学や数学に挑戦してみてはいかがでしょうか。
ちなみにshorの符号は入門的な存在で、スタビライザー符号や表面符号など、3年生にとっては懐かしのシンドロームといった単語が出てくる手法もあるので、量子誤り訂正もついでにやるとお得感があります。