大栗博司氏の著書「数学の言葉で世界を見たら」の第8話『本当にあった「空想の数」』に虚数の話があった。
2次方程式
x^2+1=0
を例に、「虚数は、このように実数の解を持たない2次方程式を解くために考えられたという解説がよくされるが、そうではない。歴史的には、虚数の考え方が数学で真剣に考えられるようになっってきたのは、2次方程式ではなく、3次方程式の解法の研究からだった。」と述べている。
そして3次方程式
x^3-6x+2=0
の例が挙げられていた。
Mathematicaでの検証
まず
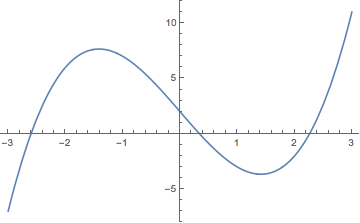
y=x^3-6x+2
のグラフを書いてみる。
Plot[x^3-6x+2, {x,-3,3}]
3次曲線がx軸に3箇所で交わっていること(3つの実数解を持つこと)がわかる。
次に3次方程式を解いてみる。
x/.Solve[x^3-6+2==0,x]
\left\{\frac{2}{\sqrt[3]{-1+i \sqrt{7}}}+\sqrt[3]{-1+i \sqrt{7}},-\frac{1+i \sqrt{3}}{\sqrt[3]{-1+i \sqrt{7}}}-\frac{1}{2} \left(1-i \sqrt{3}\right)
\sqrt[3]{-1+i \sqrt{7}},-\frac{1-i \sqrt{3}}{\sqrt[3]{-1+i \sqrt{7}}}-\frac{1}{2} \left(1+i \sqrt{3}\right) \sqrt[3]{-1+i \sqrt{7}}\right\}\
Mathematicaは思ったように分母の有理化をしてくれないのだけれど、実は
\frac{2}{\sqrt[3]{-1+i \sqrt{7}}}=\sqrt[3]{-1-i \sqrt{7}}
である。これは
ToRadicals[FullSimplify[2/(-1 + I*Sqrt[7])^(1/3)]]
で確認できる。従って
\left\{\sqrt[3]{-1-i \sqrt{7}}+\sqrt[3]{-1+i \sqrt{7}},-\frac{1}{2} \left(1+i \sqrt{3}\right) \sqrt[3]{-1-i \sqrt{7}}-\frac{1}{2} \left(1-i
\sqrt{3}\right) \sqrt[3]{-1+i \sqrt{7}},-\frac{1}{2} \left(1-i \sqrt{3}\right) \sqrt[3]{-1-i \sqrt{7}}-\frac{1}{2} \left(1+i \sqrt{3}\right)
\sqrt[3]{-1+i \sqrt{7}}\right\}
となる。3乗根の中に虚数単位 i が残っている。ところが、例えば最初の解
\sqrt[3]{-1-i \sqrt{7}}+\sqrt[3]{-1+i \sqrt{7}}
の2つの3乗根は実は複素共役であって、その和は実数。
関数Nを使って近似解を求めれば、
\{2.2618,-2.60168,0.339877\}
と実数である。なんとも不思議な話。
追記
先ほどの3次方程式の3解は各々2つの3乗根の和になっているが、それを分けた6つの数を考える。
\left\{\sqrt[3]{-1-i \sqrt{7}},\sqrt[3]{-1+i \sqrt{7}},-\frac{1}{2} \left(1+i \sqrt{3}\right) \sqrt[3]{-1-i \sqrt{7}},-\frac{1}{2} \left(1-i
\sqrt{3}\right) \sqrt[3]{-1+i \sqrt{7}},-\frac{1}{2} \left(1-i \sqrt{3}\right) \sqrt[3]{-1-i \sqrt{7}},-\frac{1}{2} \left(1+i \sqrt{3}\right)
\sqrt[3]{-1+i \sqrt{7}}\right\}
実はこの6つの数は全て方程式 $x^6+2x^3+8=0$ の解。
方程式 $x^3-6x+2=0$ とは何らかの関係があるのだろうけれど、これ以上は追求しません。(^_^;)
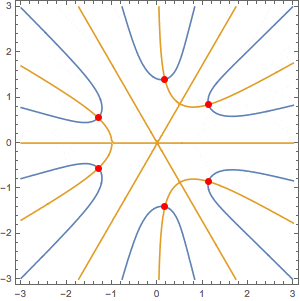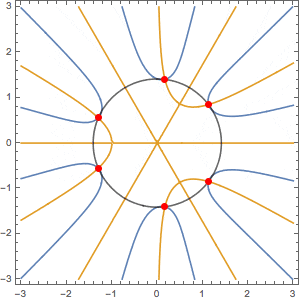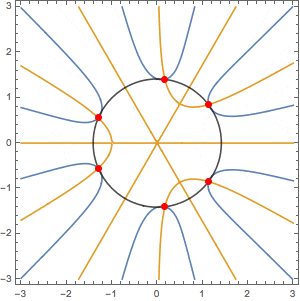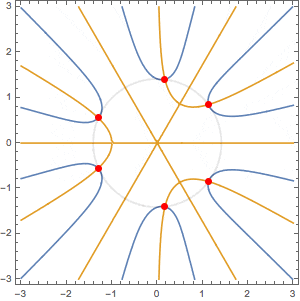
複素平面乗での6次方程式の解の配置
6次方程式 $x^6+2x^3+8=0$ の解は、絶対値と偏角で表示すると対称性があることがわかる。
\sqrt[3]{-1-i \sqrt{7}}=\sqrt{2} e^{-\frac{1}{3} i \left(\pi- \tan ^{-1}\left(\sqrt{7}\right) \right)}
\sqrt[3]{-1+i \sqrt{7}}=\sqrt{2} e^{\frac{1}{3} i \left(\pi -\tan ^{-1}\left(\sqrt{7}\right)\right)}
\frac{1}{2} \left(-1-i \sqrt{3}\right) \sqrt[3]{-1-i \sqrt{7}}=-\sqrt{2} e^{\frac{1}{3} i \tan ^{-1}\left(\sqrt{7}\right)}
\frac{1}{2} \left(-1+i \sqrt{3}\right) \sqrt[3]{-1+i \sqrt{7}}=-\sqrt{2} e^{-\frac{1}{3} i \tan ^{-1}\left(\sqrt{7}\right)}
\frac{1}{2} \left(-1+i \sqrt{3}\right) \sqrt[3]{-1-i \sqrt{7}}=\sqrt{2} e^{\frac{1}{3} i \left(\pi +\tan ^{-1}\left(\sqrt{7}\right)\right)}
\frac{1}{2} \left(-1-i \sqrt{3}\right) \sqrt[3]{-1+i \sqrt{7}}=\sqrt{2} e^{-\frac{1}{3} i \left(\pi +\tan ^{-1}\left(\sqrt{7}\right)\right)}
複素平面上に $Re(x^6+2x^3+8)=0$ の線(水色)と $Im(x^6+2x^3+8)=0$ の線(橙色)を描いてみると下図のようになる。水色線と橙線の交点(赤色)は方程式 $x^6+2x^3+8=0$ の解。絶対値 $\sqrt{2}$ の円上にある。
これは偶然、ではないですよね。