四次元立方体（正八胞体）が三次元空間を通過する様子をmatplotlibで描画

はじめに

筆者は数学もプログラミングも得意ではないため、間違っているところやもっといい感じにできるところがあれば助言お願いいたしますm(_ _)m

四次元立方体とは

四次元立方体（正八胞体）とは、我々のよく知る立方体を四次元に拡張したものです。
今回は一辺の長さが$1$であるものを考えます。

頂点は座標が$(x, y, z, u)$の各要素が$0$か$1$であることを考えれば、$2^4=16$個あることがわかります。
辺の数も数えておきましょう。$(x, y, z, u)$のうち、どれか3つを固定すると辺が一つ決まります。

例：$x=0, y=1, z=1$を固定すると、$(0, 1, 1, 0)$と$(0, 1, 1, 1)$を結ぶ辺が決まる。

例のように考えると、辺の数は${}_4C_3 \times 2^3=32$個あることがわかります。

今回やること

この記事では、

1. 四次元の方向ベクトル$\mathbf{e}$を設定する。
2. $\mathbf{e}$に対し、三次元の直交補空間を定め、原点を揃えた三次元座標系$(X, Y, Z)$を設定する。
3. 前項で設定した四次元立方体を、$-\mathbf{e}$の方向に平行移動させて、三次元座標系$(X, Y, Z)$への射影を考える。
4. matplotlibで描画し、アニメーションにしてみる

みたいなことをやります。

三次元の場合

話を簡単にするために、まずは三次元立方体について考えていきましょう。
例えば$-\mathbf{e}$が下図の黒矢印の方向だとすると、直交補空間は$\mathbf{e}$と垂直な平面なので、黄緑色の平面となる。

黄緑の平面（直交補空間）に適当な$(X, Y)$座標系をとると、下図のように三角形だったり六角形だったりというような断面になることがわかります。

では、それぞれの頂点を計算で求めることを考察してみましょう。

$|\mathbf{e}|=1$であることを仮定します。座標系$(x, y, z)$の正規直交基底を$\mathbf{e}_x=(1, 0, 0), \mathbf{e}_y=(0, 1, 0), \mathbf{e}_z=(0, 0, 1)$とします。
$\mathbf{e}$の$z$成分が非ゼロだとすると、$\mathbf{e}, \mathbf{e}_x, \mathbf{e}_y$は線型独立と言えます。
Gram-Schmidtの直交化などによって、$\mathbf{e}, \mathbf{e}_x, \mathbf{e}_y$から正規直交基底$\mathbf{e}, \mathbf{e}_X, \mathbf{e}_Y$を作ると、$\mathbf{e}_X, \mathbf{e}_Y$が$\mathbf{e}$に対する直交補空間の正規直交基底となっています。

立方体の辺と直交補空間の交点が頂点となるので、立方体が$-t\mathbf{e}$だけ平行移動したときに、辺上の点$\mathbf{r}$が直交補空間に含まれる条件を考えると、

(\mathbf{r}-t\mathbf{e})\cdot\mathbf{e}=0 \iff
\mathbf{r}\cdot\mathbf{e}=t

となります。
また、辺上の点$\mathbf{r}$は、うまく立方体の頂点座標$\mathbf{node}$(辺の端点のどちらか)を選べば、

\mathbf{r}=\mathbf{node}+a\mathbf{e}_i\ (0\leq a\leq 1,\ i:x, y, z のどれか)

と書けます。このとき、$\mathbf{node}$の$i$成分は$0$となる。$a$について解くと、

a = \frac{t - \mathbf{node}\cdot\mathbf{e}}{\mathbf{e}_i\cdot\mathbf{e}}

となり、それぞれの辺に対して$\mathbf{node}$をうまく選ぶ($\mathbf{r}(0,1,a)$に対しては$\mathbf{node}(0,1,0)$)ことによって、与えられた$t$から$a$を求めることができ、$0\leq a\leq 1$を満たせば、$\mathbf{r}$は立方体の辺と直交補空間の交点となります。

交点の$(X, Y)$座標は$X =(\mathbf{r}-t\mathbf{e})\cdot\mathbf{e}_X, Y =(\mathbf{r}-t\mathbf{e})\cdot\mathbf{e}_Y$によってそれぞれ求められます。

交点を全て求めた後は、それぞれの点が同一の面上にある場合に線分で結べば、知りたい図形の形が分かります。

四次元の場合

四次元の場合も三次元の場合と同じように考えられるはずです。

$\mathbf{e}_x=(1, 0, 0, 0), \mathbf{e}_y=(0, 1, 0, 0), \mathbf{e}_z=(0, 0, 1, 0), \mathbf{e}_u=(0, 0, 0, 1)$、$\mathbf{e}$の$u$成分が非ゼロ、$|\mathbf{e}|=1$であることを仮定します。

1. $\mathbf{e}$と$\mathbf{e}_{x, y, z}$からGram-Schmidtの直交化によって、正規直交基底$\mathbf{e}, \mathbf{e}_X, \mathbf{e}_Y, \mathbf{e}_Z$を作る。$\mathbf{e}_X, \mathbf{e}_Y, \mathbf{e}_Z$が$\mathbf{e}$に対する直交補空間を張る。

2. $a = (t - \mathbf{node}\cdot\mathbf{e})/(\mathbf{e}_i\cdot\mathbf{e})$に従って交点座標を求める。

3. 交点同士が同じ面上にあれば、線分で結ぶ。$\mathbf{p}_1$と$\mathbf{p}_2$同じ面上にあるかどうかは$(\mathbf{p}_1-\mathbf{p}_2)\cdot\mathbf{e}_i=0\ (i=x, y, z, u)$となる$i$が二つ以上あるかどうかを確認すれば良い。

といった手順で考えていきます。

サンプルコード

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d.art3d as art3d
import matplotlib.animation as animation
import itertools # 頂点・辺の生成に使用

# --- 補助関数 ---

def normalize(v):
    """ベクトルを正規化する"""
    norm = np.linalg.norm(v)
    if norm == 0:
        return v
    return v / norm

def gram_schmidt(e, basis_vectors):
    """
    ベクトルeに対して、指定された基底ベクトルから
    eに直交する正規直交基底 (eX, eY, eZ) を生成する
    """
    eX = basis_vectors[0] - np.dot(e, basis_vectors[0]) * e
    eX = normalize(eX)
    
    eY = basis_vectors[1] - np.dot(e, basis_vectors[1]) * e - np.dot(eX, basis_vectors[1]) * eX
    eY = normalize(eY)
    
    eZ = basis_vectors[2] - np.dot(e, basis_vectors[2]) * e - np.dot(eX, basis_vectors[2]) * eX - np.dot(eY, basis_vectors[2]) * eY
    eZ = normalize(eZ)
    
    return (eX, eY, eZ)

def get_lines_indices(intersection_points_4d):
    """
    4Dの交点リスト(n, 4)を受け取り、超立方体の同じ2D面 (face) 上にある
    点のペアのインデックス (i, j) (i < j) のリストを返す。
    
    「同じ面にある」 = 4D座標のうち、少なくとも2つの成分が一致する
    """
    n = len(intersection_points_4d)
    if n < 2:
        return [], []
    
    # (n, 1, 4) と (1, n, 4) のブロードキャストで差分 (n, n, 4) を計算
    diffs = intersection_points_4d[:, np.newaxis, :] - intersection_points_4d[np.newaxis, :, :]
    
    # 差分が0に近い（同じ座標成分を持つ）成分の数をカウント (n, n)
    same_coords_count = np.sum(np.isclose(diffs, 0), axis=2)
    
    # 2つ以上の座標成分が一致するペアを抽出 (i < j のみ)
    same_face_matrix = (same_coords_count >= 2)
    i_indices, j_indices = np.where(np.triu(same_face_matrix, k=1))
    
    return i_indices, j_indices

def create_line(p1, p2):
    """2つの3D点 p1, p2 を結ぶ Line3D アーティストを返す"""
    return art3d.Line3D([p1[0], p2[0]], [p1[1], p2[1]], [p1[2], p2[2]], color='c')

# --- メイン処理 ---

# 4D 標準基底
ex = np.array([1, 0, 0, 0], dtype=float)
ey = np.array([0, 1, 0, 0], dtype=float)
ez = np.array([0, 0, 1, 0], dtype=float)
eu = np.array([0, 0, 0, 1], dtype=float)
original_basis = [ex, ey, ez] # グラムシュミットの元

# (1) 方向ベクトルの入力
print('方向ベクトル(x, y, z, u)を入力してください。(u>0。他の要素は非負。半角スペース区切り。)')
try:
    e_input = np.array(list(map(float, input().split())))
    if len(e_input) != 4 or e_input[3] <= 0 or np.any(e_input[:3] < 0):
        raise ValueError("入力条件 (u>0, x,y,z>=0) を満たしていません。")
except Exception as err:
    print(f"入力エラー: {err}")
    print("デフォルト値 (1, 1, 1, 1) を使用します。")
    e_input = np.array([1, 1, 1, 1], dtype=float)

e = normalize(e_input)

# (2) 超立方体の頂点と辺を生成
# 頂点 (16, 4)
nodes = np.array(list(itertools.product([0, 1], repeat=4)), dtype=float)

# 辺 (32, 2, 4)
edges = []
for i, j in itertools.combinations(range(16), 2):
    # ハミング距離（座標の差が1の成分の数）が1のペアを探す
    if np.sum(np.abs(nodes[i] - nodes[j])) == 1:
        # 辺の方向を揃える (座標和が小さい方 -> 大きい方)
        if np.sum(nodes[i]) < np.sum(nodes[j]):
            edges.append([nodes[i], nodes[j]])
        else:
            edges.append([nodes[j], nodes[i]])
edges = np.array(edges) # (32, 2, 4)

# 辺の始点 (32, 4) と方向ベクトル (32, 4)
edge_nodes1 = edges[:, 0, :]
edge_dirs = edges[:, 1, :] - edge_nodes1

# (3) 射影基底の準備
eX, eY, eZ = gram_schmidt(e, original_basis)
projection_basis = np.array([eX, eY, eZ]) # (3, 4)

# (4) 描画設定
fig = plt.figure(figsize=(10, 7), dpi=120)
ax = fig.add_subplot(111, projection='3d')
ax.set_box_aspect((1, 1, 1))

# 射影空間のスケールを合わせる (超立方体は (0,0,0,0)-(1,1,1,1) にある)
# 射影後の座標の最大/最小値を見積もるのは難しいため、
# 元のコードに合わせて [-1, 1] に設定
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.set_zlim(-1, 1)
ax.set_xlabel("X (projection)")
ax.set_ylabel("Y (projection)")
ax.set_zlabel("Z (projection)")

# (5) アニメーションループ
ims = []
# t の範囲: 0 (p=(0,0,0,0)の時) から e.(1,1,1,1) (p=(1,1,1,1)の時) まで
t_max = np.dot(e, np.array([1, 1, 1, 1]))
t_values = np.linspace(0, t_max, 200)

# ゼロ除算警告を抑制 (計算上、該当箇所はマスクで除外するため)
with np.errstate(divide='ignore', invalid='ignore'):
    for t in t_values:
        im = [] # このフレームで描画するアーティスト

        # (5-1) 交点計算 (ベクトル化)
        # np.dot(e, edge.dir)
        dot_e_dir = np.dot(edge_dirs, e)   # (32,)
        # np.dot(e, edge.node1.r)
        dot_e_node1 = np.dot(edge_nodes1, e) # (32,)

        # a = (t - np.dot(e, edge.node1.r)) / np.dot(e, edge.dir)
        a = (t - dot_e_node1) / dot_e_dir # (32,)
        
        # 辺の内分点 (0 <= a <= 1) であり、かつ超平面が辺と平行でない
        # (浮動小数点の誤差を許容)
        valid_mask = (a >= -1e-9) & (a <= 1 + 1e-9) & ~np.isclose(dot_e_dir, 0)
        
        # 有効な交点 (4D)
        intersection_list_4d = edge_nodes1[valid_mask] + a[valid_mask, np.newaxis] * edge_dirs[valid_mask]

        if len(intersection_list_4d) == 0:
            ims.append(im) # 空のフレームを追加
            continue

        # (5-2) 3Dへの射影 (ベクトル化)
        # p' = p - t*e (超平面上のベクトルに)
        p_centered = intersection_list_4d - t * e
        # 射影: (x, y, z) = (p'.eX, p'.eY, p'.eZ)
        # (N, 4) @ (4, 3) -> (N, 3)
        projected_intersection_list_3d = np.dot(p_centered, projection_basis.T)

        # (5-3) 描画する辺の決定 (ベクトル化)
        i_indices, j_indices = get_lines_indices(intersection_list_4d)
        
        # (5-4) 描画
        for i, j in zip(i_indices, j_indices):
            p1 = projected_intersection_list_3d[i]
            p2 = projected_intersection_list_3d[j]
            line = create_line(p1, p2)
            im.append(ax.add_line(line)) # add_line はアーティストを返す
        
        ims.append(im)

# (6) アニメーション実行
ani = animation.ArtistAnimation(fig, ims, interval=10, blit=False) # blit=True は 3D だと問題が起きがち
plt.show()

結果

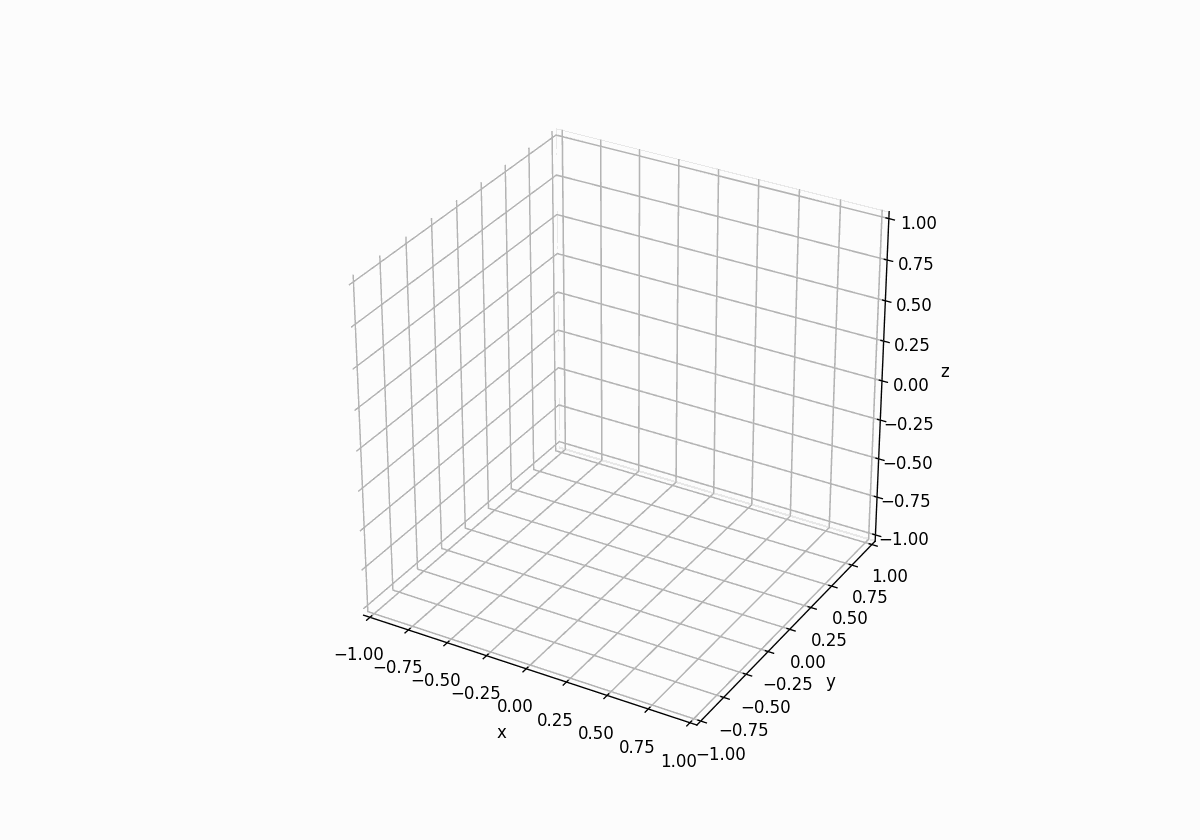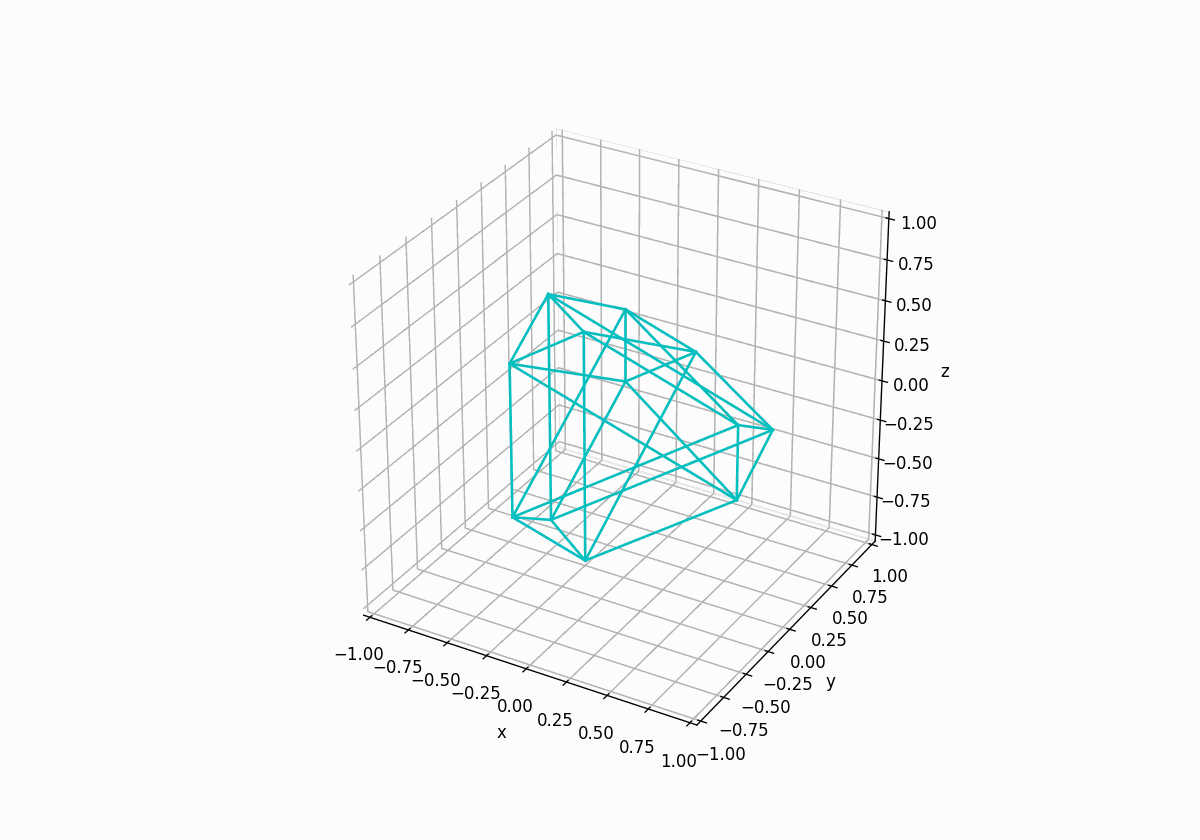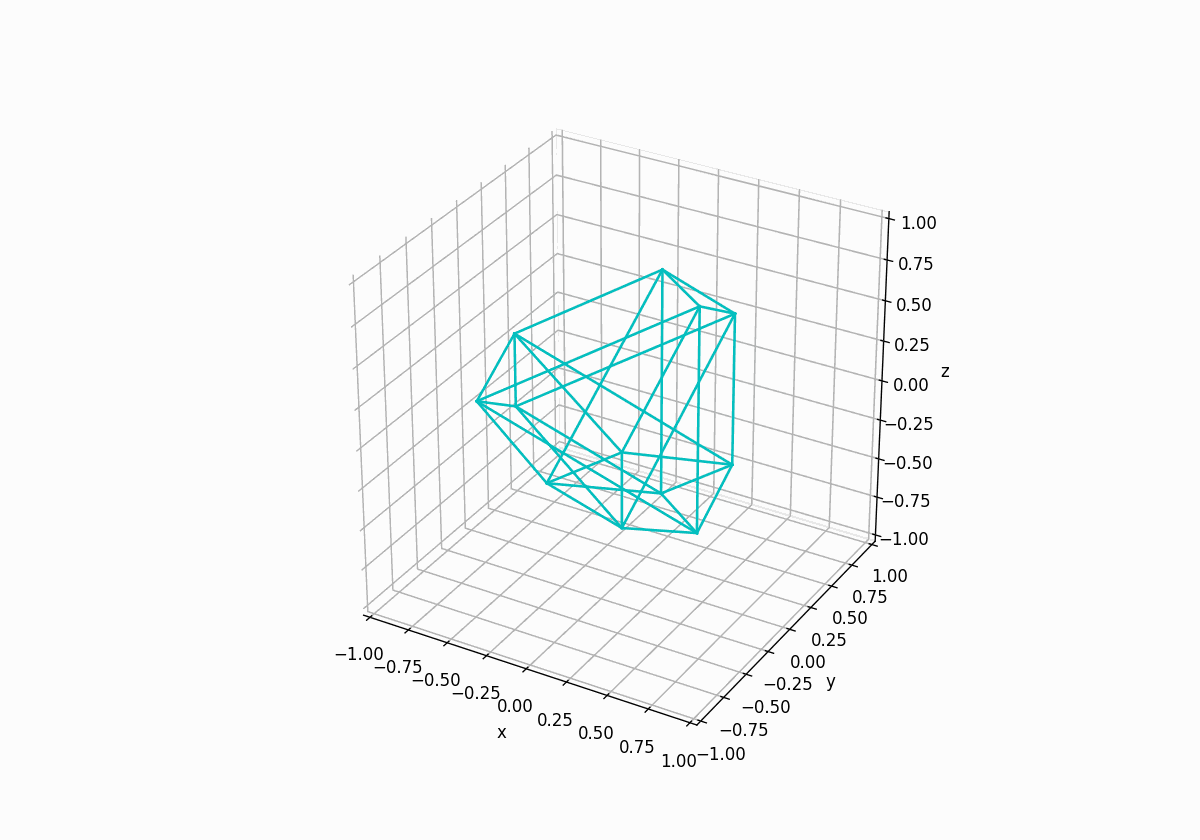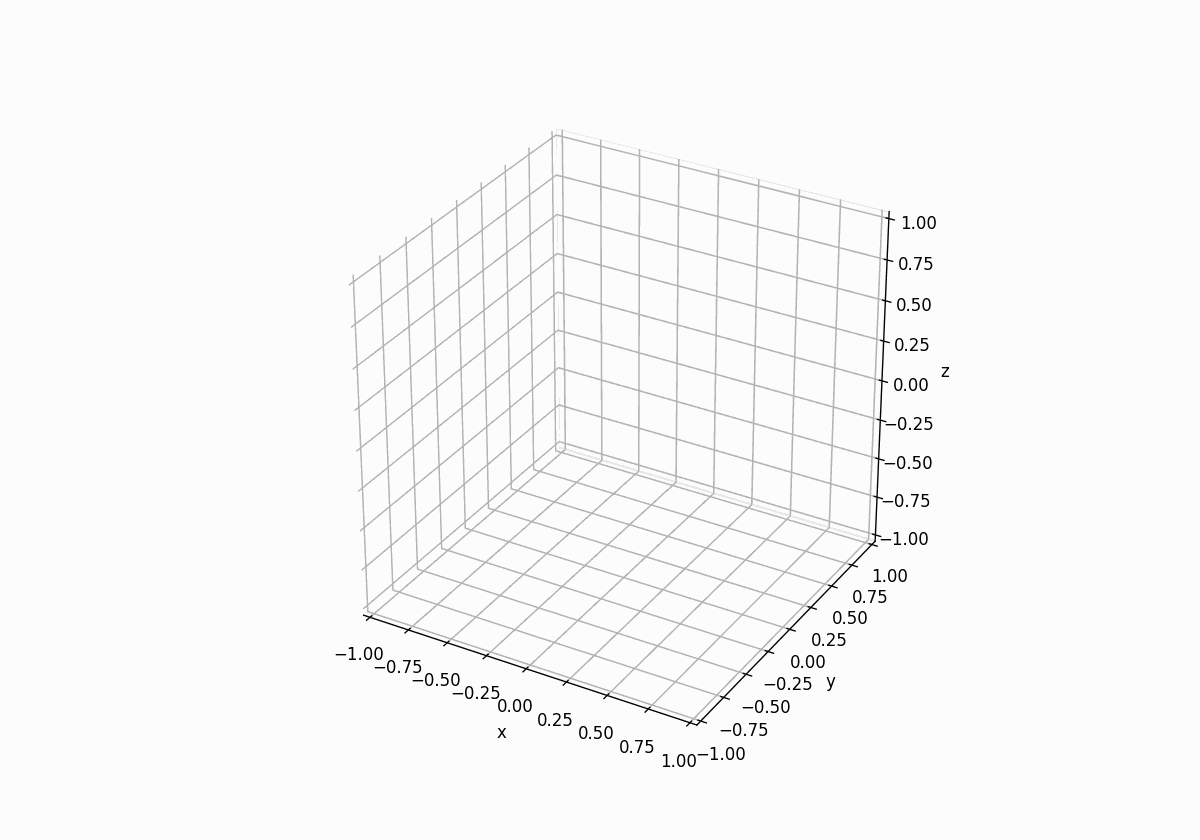
入力を$(1, 1, 1, 1)$とした場合のアニメーションはこのようになりました。

正四面体→正八面体→正四面体のように変化しています。三次元の場合は正三角形→正六角形→正三角形のように変化することと似ていますね。

皆さんも色々入力を変えて試してみてください。