LoginSignup
4
6

More than 1 year has passed since last update.

@tax_nalgoin日本アルゴリズム株式会社

量子コンピュータで論理パズルを解いてみた

Last updated at Posted at 2023-04-24

概要

本記事は

  • Qiskit公式テキストブックに載っている「Groverのアルゴリズム」のコードを改造して、
  • 嘘つきを見つける論理パズルを解いてみた

ものです。

量子アルゴリズムについて書かれた記事は既にいくつもありますが、
では「それらを用いて実際の問題を解くにはどうすればよいのか？」が気になりまして、
勉強ついでに量子コンピュータで簡単な論理パズルを解いてみました。

環境

本記事で出てくるコードはGoogle Colaboratory上で動作確認したものです。
各バージョンは以下となっています。

import qiskit.tools.jupyter
%qiskit_version_table
qiskit_version_table の結果
Version Information
  Qiskit Software		Version
  qiskit-terra			0.23.3
  qiskit-aer			0.12.0
  qiskit-ibmq-provider	0.20.2
  qiskit				0.42.1
System information
  Python version	3.9.16
  Python compiler	GCC 9.4.0
  Python build		main, Dec 7 2022 01:11:51
  OS				Linux
  CPUs				1
  Memory (Gb)		12.681190490722656
Wed Apr 12 07:42:33 2023 UTC

量子コンピュータとは

量子コンピュータが何かなどの細かな説明はQiitaの1記事で書ききれるものではないため、記事の末尾に記載している参考文献をご参照ください。
その上で軽く説明すると、量子コンピュータは文字通り 量子を用いたコンピュータ のことです。

量子コンピュータでは 量子ビット と呼ばれるものに情報を格納し、その量子ビットを 量子回路 で操作することで、量子ビットの状態を求める回答に変化させます。
この量子ビットが従来のコンピュータにおけるビットと異なり、 0と1を重ね合わせたまま 計算ができるということで、
従来のコンピュータでは解くのが難しい問題も、量子コンピュータなら解くことができると期待されています。

Groverのアルゴリズム

Groverのアルゴリズムが何かについては、Qiskit公式テキストブックを見るのが手っ取り早いです。

ざっくり解説すると、 ソートもインデックスも無いデータベースを検索する量子アルゴリズム がGroverのアルゴリズムです。
このような計算をする場合、従来のコンピュータでは $O(n)$ の計算量となりますが、本アルゴリズムなら $O(\sqrt{n})$ で済むのが特徴です。

またこのアルゴリズムは検索問題以外にも応用できます。
例えば上記ドキュメントには $2 \times 2$ のミニ数独を解く例が載っています。
これまたざっくり解説すると、以下の手順で解くことができます。

  1. 数独におけるルール（行/列に同じ数字がない）が 満たされているかをチェックする 量子回路をつくる
  2. 位相キックバックというものを使って、上記チェック回路をGroverのアルゴリズムで使える形（オラクル）に変換する
  3. 変換したオラクルをGroverのアルゴリズムに与えて実行する

細かな説明は上記URLなどを参照していただくとして、
ここで重要なのは 解きたい問題をチェックする量子回路がうまく作れたら、Groverのアルゴリズムで解くことができる ということです。

今回はその例として、嘘つきを見つける論理パズルを解いてみたいと思います。

Groverのアルゴリズムで嘘つきを見つける

問題設定と従来の解き方

まず問題は以下とします。

問題文
ここに悪魔が1人と天使が2人います。
悪魔は必ず嘘を付き、天使は必ず真実を述べます。
誰が悪魔であるかはわかっていません。

各人が以下のような証言をしているとき、誰が悪魔かを当ててください。

A: Cは悪魔である
B: Aは天使である
C: Bは悪魔である

よくあるパズルですが、順を追って解いてみると以下の通りになります。

  • まず、Aが悪魔である場合を考える
    1. 「Cは悪魔である」は嘘なのでCは天使
    2. Cが天使とすると「Bは悪魔である」は真実であるが、その場合悪魔が2人になるので不正解
  • 次に、Aが天使である場合を考える
    1. 「Cは悪魔である」は真実なのでCは悪魔
    2. Cが悪魔とすると「Bは悪魔である」は嘘なのでBは天使
    3. Bが天使とすると「Aは天使である」は真実であり、Aは天使と仮定しているため正解

したがって正解は Cが悪魔 ですが、これを見ると分かる通り、
「Aが悪魔/天使だった場合どうなるか」のように パターン分けして検証しなければ解くことができません。
従来のコンピュータで解く場合も、同様に「Aは悪魔か」を仮定して解いていく形になるかと思います。

一方量子コンピュータでは先に述べたとおり、「Aが悪魔/天使」という情報を重ね合わせたまま解くことができます。

量子アルゴリズムとしての解き方

前述した数独を解くアルゴリズムと大体同じです。
すなわち以下を チェックする量子回路 を作れば解くことができます。

  • 各人の証言が全て満たされていること
  • 悪魔が1人だけであること

各種定義

これらをチェックする回路として、以下の量子ビットを定義します。

量子ビットの定義
# 各人が天使(0)か悪魔(1)かを保持する3ビット
var_qubits = QuantumRegister(3, name='v')

# 各人の証言の真偽を保持する3ビット + 悪魔が1人であるかを保持する1ビット
# どのビットも、偽=0/真=1 と定義する
clause_qubits = QuantumRegister(3 + 1, name='clauses')

# clause_qubitsが全て1であるかを保持する1ビット
# 全て1なら全ての条件が真であるため、それが正解となる
output_qubit = QuantumRegister(1, name='out')

# 結果出力用の3ビット
cbits = ClassicalRegister(3, name='cbits')

そして、各人の証言は以下のように定義します。

証言のコード的表現
# [証言先(A=0, B=1, C=2), 天使(0)か悪魔(1)か]の形式で保持
clauses = [
    [2, 1], # A=0番目の人は「C=2が悪魔=1」であると証言
    [0, 0], # B=1番目の人は「A=0が天使=0」であると証言
    [1, 1]  # C=2番目の人は「B=1が悪魔=1」であると証言
]

各人の証言をチェックする回路

このとき、例えば1つ目の証言である「A: Cは悪魔である」をチェックする回路は以下のようになります。

image.png

これまた細かいところはQiskitのサイトを確認いただくとして、この回路は v0 != v2ならclauses0を反転させる 回路となります。
また全てのclausesビットは初期値が0なので、結果として v0 != v2であるかをチェックする 回路となります。
なぜこれが「A: Cは悪魔である」ことをチェックしているかは、AとCがどのような値を取るかを見ればわかります。

A C A != C 「A: Cは悪魔である」
天使(0) 天使(0) False 偽
天使(0) 悪魔(1) True 真
悪魔(1) 天使(0) True 真
悪魔(1) 悪魔(1) False 偽

この回路や表にあるAやCは任意のものに書き換えても成り立ちますから、
この回路は「は悪魔である」系の証言全てに使える回路となります。

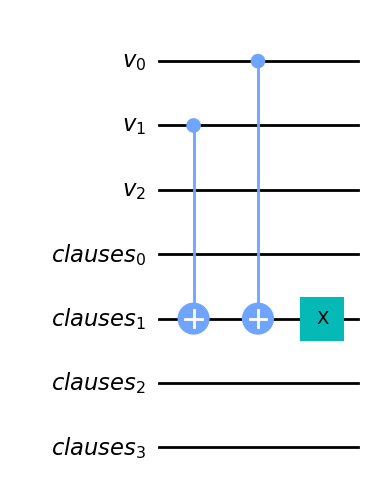
また同様の理由により、「は天使である」系の証言は v0 = v2であるかをチェックする 回路を作れば良いことになります。
その回路は以下のとおりです。

image.png

この回路の X は 対象量子ビットを反転させる ものです。
v0 != v2であるかをチェックする 回路の結果を反転させるので、v0 == v2であるかをチェックする 回路となります。

悪魔が1人であるかをチェックする回路

悪魔が1人であるかは、以下を全て満たすかどうかでチェックできます。
（少し回りくどい方法なので、もっとスマートな回路があるかもしれません。）

  • 3人とも悪魔ではないこと
  • 悪魔が奇数人であること

これを満たす回路は以下の通りです。

image.png

線でつながっている全ての●が1の場合に対となる＋のビットを反転するので、

  • v0, v1, v2が全て1なら反転
  • v0が1なら反転
  • v1が1なら反転
  • v2が1なら反転

という回路となります。
結果として、悪魔が1人である場合にのみclauses3が1となります。

回路全体と実行結果

あとは数独の回路とほぼ同じアルゴリズムになります。
そのため説明は省略して、回路全体とそのソースコードを以下に示すにとどめます。

image.png

量子コンピュータで論理パズルを解くコード（長いので折りたたみ）

実行に必要なライブラリは以下の通りです。

!pip install pylatexenc numpy qiskit
量子コンピュータで論理パズルを解くコード
import numpy as np

from qiskit import IBMQ, Aer, transpile, execute
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit.providers.ibmq import least_busy
from qiskit.visualization import plot_histogram

# 問題設定:
# 3人のうち1人が嘘つきで、各人の証言は以下の通り。
# 0番: 2番は嘘つき
# 1番: 0番は嘘つきではない
# 2番: 1番は嘘つき

# 条件設定: [対象ビット, 嘘つきなら1]
clauses = [[2, 1], [0, 0], [1, 1]]

def qc_xor(qc, a, b, output):
    """output = a xor b"""
    qc.cx(a, output)
    qc.cx(b, output)

def lie_detector(qc, clause, i, var_qubits, clause_qubits):
    """
    1人の証言を量子回路に落とし込む

    Args:
        clause: 1つの証言
        i: 証言している人の番号
        var_qubits: 証言をしている人が嘘つきかどうか
        clause_qubits: 証言されている人
    """
    qc_xor(qc, var_qubits[i], var_qubits[clause[0]], clause_qubits[i])
    if clause[1] == 0:
        qc.x(clause_qubits[i])

def oracle(qc, clause_list, var_qubits, clause_qubits, output_qubit):
    for i, clause in enumerate(clauses):
        lie_detector(qc, clause, i, var_qubits, clause_qubits)

    qc.mcx(var_qubits, clause_qubits[-1])
    for v in var_qubits:
        qc.cx(v, clause_qubits[-1])

    qc.mcx(clause_qubits, output_qubit)

    for i, clause in enumerate(clauses):
        lie_detector(qc, clause, i, var_qubits, clause_qubits)

    qc.mcx(var_qubits, clause_qubits[-1])
    for v in var_qubits:
        qc.cx(v, clause_qubits[-1])

def diffuser(nqubits):
    qc = QuantumCircuit(nqubits)
    # Hゲートで |s> -> |00..0> に変換
    for qubit in range(nqubits):
        qc.h(qubit)
    # Xゲートで |00..0> -> |11..1> に変換
    for qubit in range(nqubits):
        qc.x(qubit)
    # マルチ制御Zゲートをかけます
    qc.h(nqubits-1)
    qc.mct(list(range(nqubits-1)), nqubits-1)  # マルチ制御トフォリ
    qc.h(nqubits-1)
    # |11..1> -> |00..0> に変換
    for qubit in range(nqubits):
        qc.x(qubit)
    # |00..0> -> |s> に変換
    for qubit in range(nqubits):
        qc.h(qubit)
    # Diffuserをゲートにします
    U_s = qc.to_gate()
    U_s.name = "U$_s$"
    return U_s

var_qubits = QuantumRegister(3, name='v')
clause_qubits = QuantumRegister(3 + 1, name='clauses')
output_qubit = QuantumRegister(1, name='out')
cbits = ClassicalRegister(3, name='cbits')
qc = QuantumCircuit(var_qubits, clause_qubits, output_qubit, cbits)

qc.initialize([1, -1] / np.sqrt(2), output_qubit)

qc.h(var_qubits)
qc.barrier()

for i in range(2):
    oracle(qc, clauses, var_qubits, clause_qubits, output_qubit)
    qc.barrier()
    qc.append(diffuser(3), [0, 1, 2])

qc.measure(var_qubits, cbits)

aer_sim = Aer.get_backend('aer_simulator')
transpiled_qc = transpile(qc, aer_sim)
result = aer_sim.run(transpiled_qc, shots=1024).result()
plot_histogram(result.get_counts())

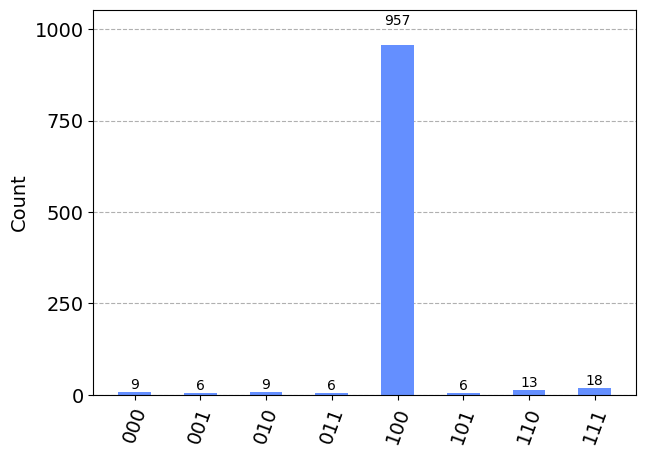
これを実行した結果は以下の通りになります。

image.png

量子コンピュータは結果を確率でしか出力できないため、上記は1024回実行した結果をヒストグラムにしたものになります。
下段にあるビット列は右から（上から）順にA, B, Cを表しますので、この回路は Cが悪魔である と出力されています。

なお、本来は100が100%正解になる回路のはずですが、
現状の量子コンピュータでは計算の誤り訂正が十分にできないために、100%とならないようです。

[2023/04/25追記] 記事に誤りがありました。失礼致しました。

  • 今回はAerシミュレータで動かしているので、ノイズは無いはずでした。
    https://qiskit.org/documentation/locale/ja_JP/tutorials/simulators/1_aer_provider.html
  • Groverのアルゴリズムでは、振幅増幅を繰り返す回数が最適な値の場合にのみ100%正解となるようです。
    今回は2回繰り返していますが、これが最適な値でない（最適な値が整数でない）可能性があります。

まとめ

以上より、Groverのアルゴリズムを用いた量子コンピュータで論理パズルを解くことができました。
重要な要素をまとめると以下になると思います。

  • 正しく解けていることをチェックする量子回路 さえ作れたら、Groverのアルゴリズムで色々な問題が解ける
  • 嘘つきを見つけるパズルも同様に、以下をチェックする回路を作ることで問題を解くことができた
    • 各人の証言が全て満たされていること
    • 悪魔が1人だけであること

なお今までの内容を見て、量子コンピュータで問題を解くには 従来のアルゴリズムとは全く異なるアプローチが必要だなあ と思いました。
その取っ掛かりを掴むまで苦戦しましたが、掴んでしまえばパズルのようでとても面白かったです。

量子コンピュータはいくつも課題が残っているそうで、まだ従来のコンピュータ同様の気軽さで使うのは難しそうですが、
今後の技術革新に期待したいなあと思う次第であります。

参考文献

Qiskit公式テキストブック
https://qiskit.org/textbook/ja/preface.html

東京大学素粒子物理国際研究センター（ICEPP）が執筆した入門教材
https://utokyo-icepp.github.io/qc-workbook/welcome.html

4
6
2

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
6