はじめに
CS専攻のM2の者です。普段は画像処理が中心ですが、先日時系列データを扱う機会がありましたので備忘録として残しておきます。時系列データの処理をやってみたい方の参考に少しでもなればと思います。数式等は省いていますので雰囲気を掴みたい方向けだと思います。また、ミス等がありましたらご指摘ビシバシお願いします。
時系列データとは
時系列データとは、**「ある一定の間隔で測定された結果の集まり」**です。気温の変化や降水量、店舗の売り上げの情報に加えて、それが測定された時間の情報をセットで持っているイメージです。
時系列データに使えるモデル+用語
ARモデル(自己回帰モデル)
- 将来のyは、過去のyによって説明される
- 過去の自分のデータを説明変数とする
- 過去のデータに係数をかけたものをいくつか組み合わせて注目するデータを表現
- 定常過程が前提
MAモデル(移動平均モデル)
- 将来のyは過去の誤差によって説明される
- 将来の予測値は過去の予測値と実績値との誤差により決まる
- (例)今月の売り上げ量が、本来の売り上げる量より多かったら、来月の売り上げ量は増える
- 注目しているデータと過去のデータに共通する項を持たせることで関係性を表現
- 定常過程が前提
ARMAモデル(自己回帰移動平均モデル)
- AR + MA 過程、いずれかの強い方の性質に従う
- そのため自己相関、偏自己相関はともにラグの大きさに応じて減衰していく
- ARMAモデルは、データ系列の定常性の下で推定や予測を行うが、現実データは非定常が多い。
- 定常過程が前提
ARIMAモデル(自己回帰和分移動平均モデル)
- ARMAモデルとの違いは、差分過程を組み込んでいる点
- ARMAに何階差分をとれば定常になるかを付与したもの
- d階差分をとった系列が定常かつ反転可能なARMA(p,q)過程に従う過程
SARIMAモデル(季節自己回帰和分移動平均モデル)
- ARIMAとの違いは、季節性を考慮するかどうか?
- 時系列方向のARIMA(p,d,q)に加え、季節性差分方向ARIAM(P,D,Q),さらに周期s
単位根(Unit root process)
- 値が足し合わされて出来上がったデータである
- 単位根を持つデータを「単位根過程」と呼ぶ
- ex) ランダムウォーク(ホワイトノイズの累積和)
- ホワイトノイズ : 自己相関も何もない、正規分布に従ったただの「ノイズ」
ADF検定
- 多くの時系列モデルでは定常過程を前提としているので時系列に対してまず最初に単位根を確認する事が多い
- 帰無仮説:単位根過程, 対立仮説 : 定常過程
- P値が0.05以下なら帰無仮説が棄却され、定常過程になる
- 一般的に「差分系列」をとったり、「対数変換」すると、その系列は定常性を持ちやすくなる
自己相関( ACF : Autocorrelation Function )
- 過去の値が現在のデータにどのくらい影響しているか?
- ズラしたデータのステップ数をラグと呼ぶ
偏自己相関( PACF : Partial Autocorrelation Function)
- 自己相関係数から時間によって受ける影響を除去した自己相関
- 今日と2日前の関係には間接的に1日前の影響が含まれる
- 偏自己相関を使うと、1日前の影響を除いて今日と2日前だけの関係を調べる事ができる
コレログラム
- ラグ+自己相関
分析
import numpy as np
import pandas as pd
日付の扱い
pd.date_range('2020-1-1', freq='D', periods=3)
'''
DatetimeIndex(['2020-01-01', '2020-01-02', '2020-01-03'], dtype='datetime64[ns]', freq='D')
'''
df = pd.Series(np.arange(3))
df.index = pd.date_range('2020-1-1', freq='D', periods=3)
df
'''
2020-01-01 0
2020-01-02 1
2020-01-03 2
Freq: D, dtype: int64
'''
idx = pd.date_range('2020-1-1',freq='D',periods=365)
df = pd.DataFrame({'商品A' : np.random.randint(100, size=365),
'商品B' : np.random.randint(100, size=365)},
index=idx)
df
'''
商品A 商品B
2020-01-01 99 23
2020-01-02 73 98
2020-01-03 86 85
2020-01-04 44 37
2020-01-05 67 63
... ... ...
2020-12-26 23 25
2020-12-27 91 35
2020-12-28 3 23
2020-12-29 92 47
2020-12-30 55 84
365 rows × 2 columns
'''
# 特定の日付のデータ取得
df.loc['2020-2-3']
'''
商品A 51
商品B 46
Name: 2020-02-03 00:00:00, dtype: int64
'''
# スライスによるデータ取得
df.loc[:'2020-1-4']
'''
商品A 商品B
2020-01-01 99 23
2020-01-02 73 98
2020-01-03 86 85
2020-01-04 44 37
'''
df.loc['2020-1-4':'2020-1-7']
'''
商品A 商品B
2020-01-04 44 37
2020-01-05 67 63
2020-01-06 6 94
2020-01-07 47 11
'''
df.loc['2020-1']
'''
### ``1月分のデータ全部表示(省略)
'''
# 月の取得
df.index.month
'''
Int64Index([ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
...
12, 12, 12, 12, 12, 12, 12, 12, 12, 12],
dtype='int64', length=365)
'''
簡単なデータ分析
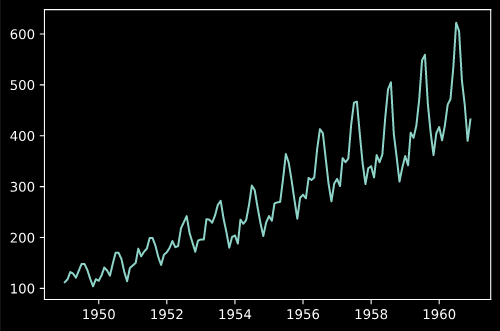
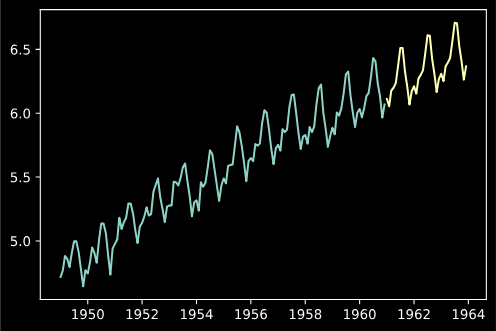
今回は時系列データで有名な'AirPassengers'のデータセットを使用します。
データの読み込みと表示
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = pd.read_csv('AirPassengers.csv', index_col=0, parse_dates=[0])
plt.plot(data)
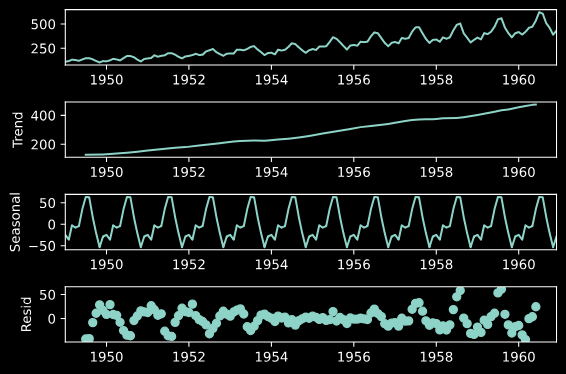
statsmodelsを利用し、trend, seasonal, residへ分解
import statsmodels.api as sm
res = sm.tsa.seasonal_decompose(data)
fig = res.plot()
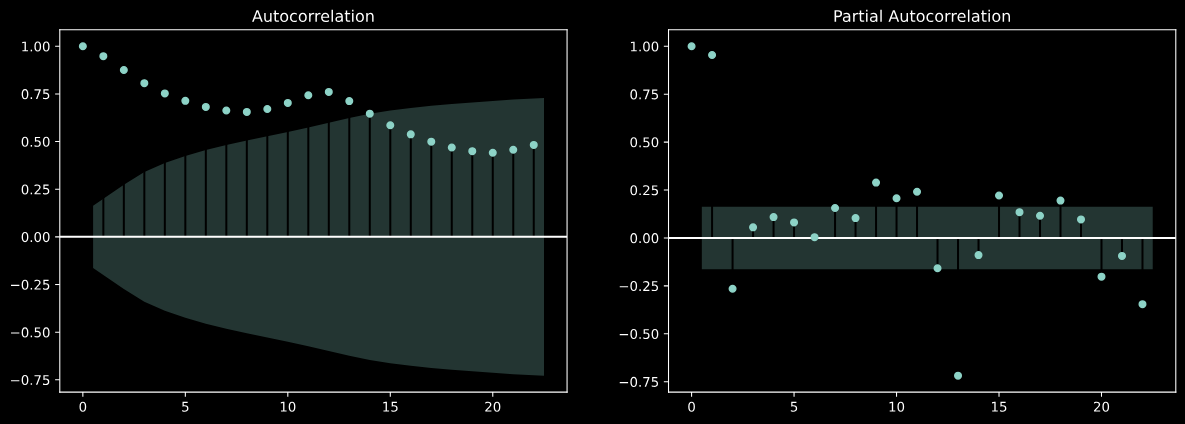
自己相関と偏自己相関の表示
fig, axes = plt.subplots(1,2, figsize=(15,5))
sm.tsa.graphics.plot_acf(data, ax=axes[0])
sm.tsa.graphics.plot_pacf(data, ax=axes[1])
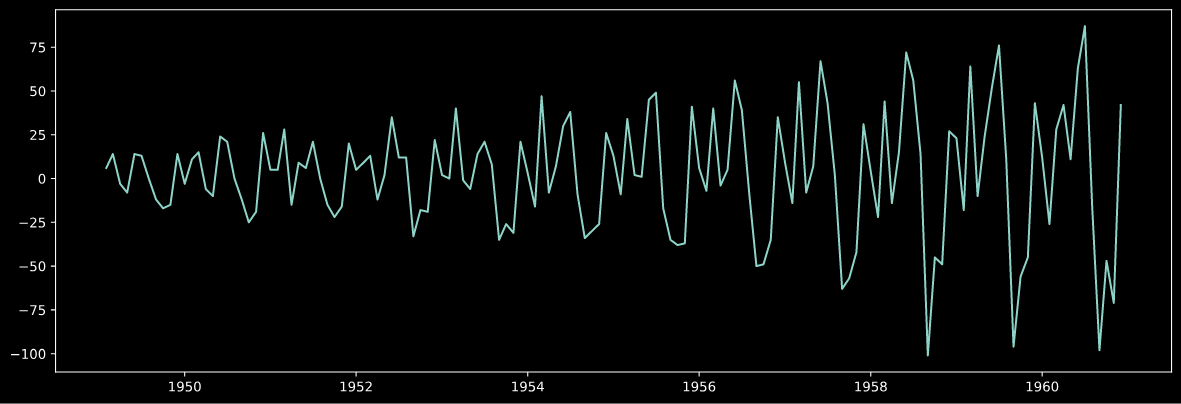
トレンドの除去
plt.figure(figsize=(15,5))
plt.plot(data.diff(1))
ADF検定
タプルで値が返ってくるのでそれの1番目の要素がP値になります。
P値が0.05以下だと帰無仮説を棄却できます。
# 元データ
sm.tsa.adfuller(data)[1]
0.991880243437641
# 対数変換
ldata = np.log(data)
sm.tsa.adfuller(ldata)[1]
0.42236677477039125
# 対数変換+階差
sm.tsa.adfuller(ldata.diff().dropna())[1]
0.0711205481508595
SARIMAモデルの推定
orderとseasonal_orderでパラメータを設定。
fit()でモデルの学習。
学習範囲外の予想は、forecast()
学習データを含む点の予測はpredict()
パラメータのチューニングは総当たりで計算した方が良い。
(statsmodelsないの関数はベストなモデルが見つけれらない?)
model = sm.tsa.SARIMAX(ldata, order=(1,1,1),seasonal_order=(0,1,2,12))
res_model = model.fit()
pred = res_model.forecast(36)
plt.plot(ldata, label='Original')
plt.plot(pred, label='Pred')
時系列データにおける特徴量作成
時系列で特徴量になりそうな情報
- 月
- 曜日
- 週数
- 週末フラグ
- 祝日
- 休日
- 気象
- 連休フラグ
- 連休何日目 etc...
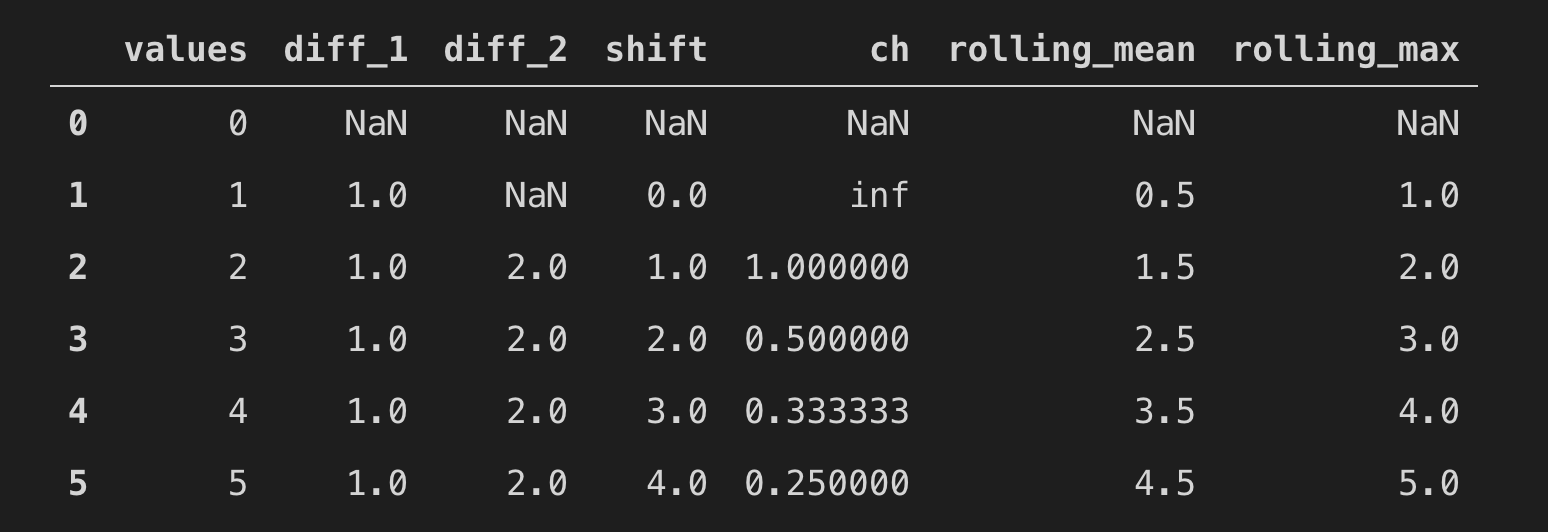
# 簡単なテーブル作成
df = pd.DataFrame(np.arange(6).reshape(6, 1),columns=['values'])
# 差分
df['diff_1'] = df['values'].diff(1)
# 2回分の差分
df['diff_2'] = df['values'].diff(2)
# 値をshiftさせるだけ
df['shift'] = df['values'].shift(1)
# 変化率
df['ch'] = df['values'].pct_change(1)
# 窓関数で移動平均
df['rolling_mean'] = df['values'].rolling(2).mean()
df['rolling_max'] = df['values'].rolling(2).max()
その他のメモ
-
tsfreshというライブラリで特徴量作成可能 - sklearnの
TimeSeriesSplitでCVできる - 機械学習系のモデルは、定常過程を過程しているから統計的なモデルの方が良いのでは?
- SARIMAモデルはnan扱えない
参考文献
終わりに
簡単にですが、時系列についてまとめてみました。気になるところは機械学習モデルと統計モデルどちらを採用すべきかですね。個人的には、統計モデルの方が結果としては良いように感じています(今回のデータではありませんが、、、)。