円形断面及び薄板円筒断面の軸力-曲げ耐力計算

1. 初めに

円筒断面のN-M曲線を計算する際に、毎回必要に迫られて計算式を作成するので、整理しておきます。

2. 対象とする断面形状

厚肉の円筒断面と薄肉の円筒断面を対象とします。厚肉の円筒断面は外側の円形断面から内側の円形断面を差し引くことで計算可能です。薄肉円筒断面は円周上に板厚tの薄板として計算します。

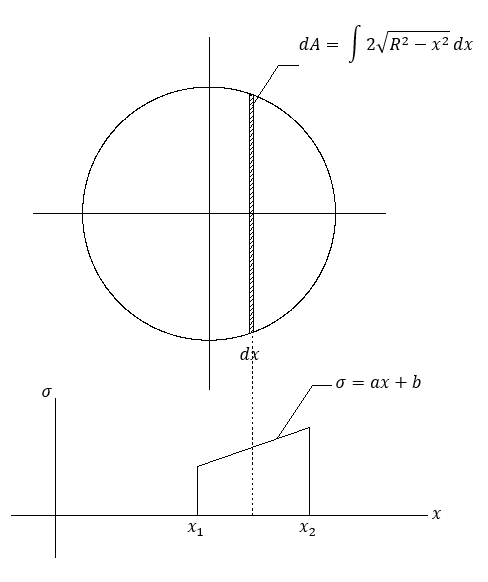
3. 円形断面

円の半径Rとします。

N = \int_{x1}^{x2} \sigma (x) \cdot A(x) dx \\
=\int (ax+b) \cdot \sqrt{R^2 - x^2} dx \\
= \left[
-\frac{a}{3} ( R^2 - x^2 )^ \frac{3}{2} + \frac{b}{2} \biggl( R^2 \cdot \sin^{-1} \frac{x}{R} + R \cdot x \cdot \sqrt{ 1 - \frac{x^2}{R^2}}  \biggr)
\right]_{x1}^{x2}
\\

M = \int_{x1}^{x2} x\cdot \sigma (x) \cdot A(x) dx\\
=\int_{x1}^{x2} (ax+b) \cdot x \cdot \sqrt{R^2 - x^2} dx\\
= \left[
 \frac{a}{8} \{ R^4 \sin^{-1}\frac{x}{R} - x \cdot \sqrt{R^2-x^2} \cdot (R^2-2 \cdot x^2)\}  -  \frac{b}{3} ( R^2 - x^2 )^\frac{3}{2}
 \right ]_{x1}^{x2}

def integYSg(R,a,b,x):
    '''
    ∫(ax+b)・√(R**2 - x**2) dx
    R:半径
    '''
    return -a/3*(R**2 - x**2)**(3/2) + b/2*(R**2*np.arcsin(x/R)/2 + R*x*np.sqrt(1 - x**2/R**2))

def integYSgX(R,a,b,x):
    '''
    ∫(ax+b)・x・√(R**2 - x**2) dx
    R:半径
    '''
    ans =  a/8*  (R**4*math.asin(x/R) - x * math.sqrt(R**2 - x**2) * (R**2 - 2 * x**2) ) \
        - b/3*(R**2 - x**2)**(3/2)
    return  ans

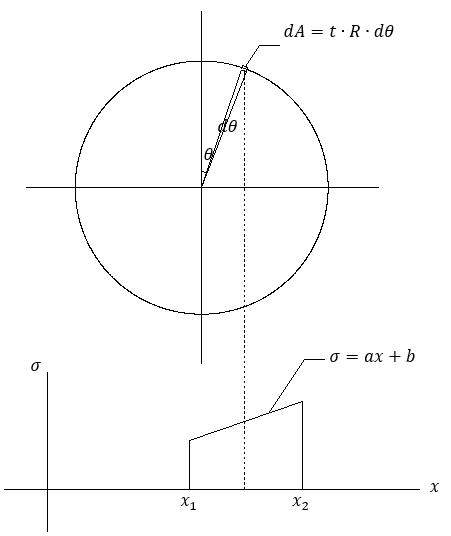
4. 薄肉円筒断面

半径R、板厚t、x=Rsinθとします。

N = \int_{\theta 1}^{\theta 2} \sigma (x) \; dA \\
= \int_{\theta 1}^{\theta 2} \sigma (x) \cdot t \cdot R \; d\theta \\
=\int ( ax+ b )\cdot t \cdot R \; d\theta \\
=\int ( a\cdot t \cdot R^2 \sin \theta + b \cdot t \cdot R ) \; d\theta \\
=\left[  -a\cdot t \cdot R^2 \cos \theta + b \cdot t \cdot R \cdot \theta \; \right]_{\theta 1}^{\theta 2}
\\

M = \int_{\theta 1}^{\theta 2} x\cdot \sigma (x) \; dA \\
=\int (ax+b) \cdot x \cdot t \cdot R \; d\theta \\
=\int (atRx^2+btRx)    \; d\theta \\
=\int (atR^3 \sin^2 \theta + btR^2 \sin \theta)    \; d\theta \\
=atR^3 \int \sin^2 \theta + btR^2 \int \sin \theta    \; d\theta \\
=atR^3 \int \frac {1-\cos2\theta}{2}  + btR^2 \int \sin \theta    \; d\theta \\
=atR^3 \left [ \frac{\theta}{2} - \frac{\sin2\theta}{4} \right]_{\theta 1}^{\theta 2} - btR^2 \left[\; \cos \theta \; \right]_{\theta 1}^{\theta 2} \\

def integRYSg(R,a,b,x):
    '''
    円弧の積分∫(ax+b)・dA
    R:半径
    板厚tを乗じる必要あり
    '''
    th  = np.arcsin(x/R)
    return -a*R**2*np.cos(th) + b*R*th

def integRYSgX(R,a,b,x):
    '''
    円弧の積分∫(ax+b)・x dA
    R:半径
    板厚tを乗じる必要あり
    '''
    th  = np.arcsin(x/R)
    return +a*R**3*(th/2-np.sin(2*th)/4) - b*R**2*np.cos(th)