画像再構成を振り返る

はじめに

サイノグラムからのフィルター補正逆投影法、MLEM、OSEMを懐かしく思い、また、引用元の文献から、知らなかった細部の知識をインプットできたので、備忘録として綴ります。

サイノグラム

今回はShepp-Loganファントム画像を使って確認していきます。

# Shepp-loganファントムの読み込み
img = skimage.data.shepp_logan_phantom()

# ファントム画像を扱いやすいサイズにリサンプリング
img = skimage.transform.resize(img, (128, 128), order=0) # order 0: Nearest-neighbor, 1: Bi-linear (default), 3: Bi-cubic

# 正規化
img = (img - img.min())/(img.max()-img.min())

この画像からサイノグラムを作成します。

# サイノグラム（Sinogram）の作成
sinogram_bin_size = 128 # ファントムの画像サイズに合わせる
# 180度の投影にします
angle = np.linspace(0, 180, sinogram_bin_size, endpoint=False)
sinogram = skimage.transform.radon(img, theta=angle)

もう少しリアルな画像をイメージして取り組みたい場合は、ノイズを入れてやります。

'''
ノイズありのサイノグラムの作成（リアルなエミッショントモグラフィっぽくノイズを加えてみる）
カウントは1000000（1e6）とする。
'''
count = 1e6
np.random.seed(76)
scale = count / sinogram.sum()
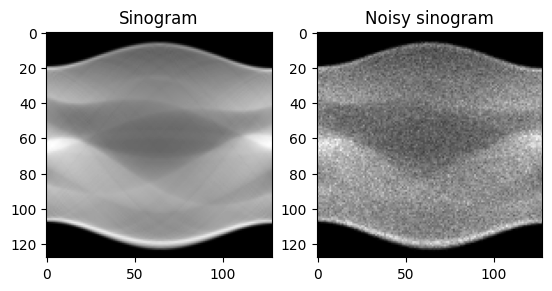
noisy_sinogram = np.random.poisson(sinogram * scale)/scale

可視化してみると、こんな感じになる。

フィルター補正逆投影法

もっとも基本的な方法と言ってもいいFiltered back projection。

# フィルター補正逆投影法（Filtered back projection, FBP）
fbp = skimage.transform.iradon(sinogram, filter_name="ramp")
noisy_fbp = skimage.transform.iradon(noisy_sinogram, filter_name="ramp")

MLEM法

確率論的なプローチを加えて、単純なFBPを発展させた方法。更新用サイノブラム（最初はまっさら）を作り、①このサイノグラムをバックプロジェクションする。②そして、実際のサイノグラムのバックプロジェクションとの比をピクセルごとに計算して、③更新用サイノグラムへ積算していく。①〜③を更新回数分繰り返す。
Maximum Likelihood Expectation Maximizationと呼ばれるのは、このように、実際のサイノグラムとの比(本物っぽさの確率)を取りながら計算するためである。
回数を重ねるごとに、元の画像のようになっていく。
単純に元のサイノグラムを再構成するよりも、低ノイズな画像を作れることがある。

# MLEM法（Maximum Likelihood Expectation Maximization）
def MLEM(sinogram, angle, N_iteration):
    eps = np.finfo(float).eps
    weight = skimage.transform.iradon(np.ones_like(sinogram), theta=angle, filter_name=None)
    mask = weight > 0
    reconstruction = np.zeros_like(weight)
    reconstruction[mask] = 1
    results = np.zeros((N_iteration, reconstruction.shape[0], reconstruction.shape[1]))
    for i in range(N_iteration):
        forward_projection = skimage.transform.radon(reconstruction, theta=angle)
        ratio = sinogram/(forward_projection+eps)
        back_projection = skimage.transform.iradon(ratio, theta=angle, filter_name=None)
        reconstruction[mask] *= back_projection[mask]/weight[mask]
        results[i,:,:] = reconstruction.copy()
        if (i+1) % 10 == 0:
             plt.imshow(reconstruction, vmin=0, vmax=1, cmap="gray")
             plt.title("MLEM: {} iteration.".format(i+1))
             plt.show()
    return results

OSEM法

MLEMを、投影角度を分割して作ったサブセットに分けて処理する方法。サブセット数が1のときはMLEM法と同義。
投影角度をサブセット数に分割し、サブセットごとに逐次処理（①〜③）を更新してから、ようやく一回分の更新となるため、MLEM(=サブセット1のときのOSEM)と比べて、収束が早まる（元のサイノグラムに似てくるスピードが早い）。
以下、直感的なコード。

def OSEM(sinogram, angle, N_iteration, n_subsets):
    eps = np.finfo(float).eps
    n_angles = len(angle)
    subset_size = n_angles // n_subsets
    subsets = [angle[i * subset_size:(i + 1) * subset_size] for i in range(n_subsets)]

    # 重みの計算
    weight = skimage.transform.iradon(np.ones_like(sinogram), theta=angle, filter_name=None)

    mask = weight > 0

    # 初期再構成
    reconstruction = np.zeros_like(weight)
    reconstruction[mask] = 1

    results = np.zeros((N_iteration, reconstruction.shape[0], reconstruction.shape[1]))

    for i in range(N_iteration):
        for subset_angle in subsets:
            subset_indices = np.isin(angle, subset_angle)
            subset_sinogram = sinogram[:, subset_indices]

            forward_projection = skimage.transform.radon(reconstruction, theta=subset_angle)
            ratio = subset_sinogram / (forward_projection + eps)
            back_projection = skimage.transform.iradon(ratio, theta=subset_angle, filter_name=None)

            reconstruction[mask] *= back_projection[mask] / weight[mask]

        results[i, :, :] = reconstruction.copy()
        if (i+1) % 10 == 0:
            plt.imshow(reconstruction, vmin=0, vmax=1, cmap="gray")
            plt.title("OSEM: {} iteration.".format(i+1))
            plt.show()

    return results

数学的な解釈は、引用文献を参考にしてほしい。

参考文献

• 橋本 二三生; 教育講座—放射線技術学研究におけるPython の活用術— 応用編　15. 画像再構成をはじめよう！, 日本放射線技術学会雑誌, 80(12) p. 1339-1343, 2024.