機械学習
コンピュータプログラムは、タスクT(アプリケーションにさせたいこと)を性能指標Pで測定し、その性能が経験E(データ)により改善される場合、タスクTおよび性能指標Pに関して経験Eから学習すると言われている。
人がプログラムするのは認識の仕方ではなく学習の仕方
1-1.線形回帰モデル
1-1-1.回帰問題
ある入力(離散あるいは連続値)から出力(連続値)を予測する問題
直線で予測→線形回帰
曲線で予測→非線形回帰
1-1-2.回帰で扱うデータ
入力(各要素を説明変数または特徴量と呼ぶ)
m次元のベクトル(m=1の場合はスカラ)
出力(目的変数)
スカラー値(目的変数)
説明変数
$x$ = ($x_1$ ,$x_2$ ,$\dots$,$x_m$)$^T$ $\in$ $\mathbb{R}^m$
目的変数
$$y\in\mathbb{R}$$
ex)住宅価格予測
説明変数:部屋数、敷地面積や築年数
目的変数:価格
回帰問題を解くためのモデルの一種
教師あり学習
入力とm次元パラメータの線形結合を出力するモデル
慣例として予測値にはハットをつける($\hat{y}$)
1-1-3.パラメータ
1.モデルに含まれる推定すべき未知のパラメータ
2.特徴量が予測値に対してどのように影響を与えるかを決定するする重みの集合
ex)正(負)の重みをつけた場合、その特徴量を増加させると、予測の値が増加(減少)
ex)重みが大きくなれば(0であれば)、その特徴量は予測に大きな影響力を持つ。(全く影響しない)
3.y軸との交点を表す。
$w$ = ($w_1$ ,$w_2$ ,・・・,$w_m$)$^T$ $\subset$ $\mathbb{R}^m$
パラメータは最小二乗法により推定
1-1-4.線形結合
入力ベクトルと未知のパラメータの各要素を掛け算し足し合わせたもの
入力ベクトルとの線形結合に加え、切片を足し合わせる
(入力のベクトルが多次元でも出力は1次元(スカラー)になる
\hat{y} = w^Tx + w_0= \sum_{j=1}^{m} w_jx_j + w_0
1-1-5.説明変数が一次元の場合(m = 1)
単回帰モデルと呼ぶ
データへの仮定
データは回帰直線に誤差が加わり観測されていると仮定
連立方程式
線形回帰は単純に連立方程式を行列の形に直しただけである。
1-1-6.説明変数が多次元の場合(m > 1)
線形重回帰モデル
単回帰は直線、重回帰は曲面
データへの仮定
データは回帰曲面に誤差が加わり観測されていると仮定
連立方程式
単回帰と全く同じ
1-2.データの分割とモデルの汎化性能測定
1-2-1.データの分割
学習用データ:機械学習モデルの学習に利用するデータ
検証用データ:学習済みモデルの精度を検証するためのデータ
分割する目的
モデルの汎化性能(Generalization)を測定するため
データへの当てはまりの良さではなく、未知のデータに対してどれくらい精度が高いかを測りたい
1-2-2.線形回帰モデルのパラメータは最小二乗法で推定
平均二乗誤差
小さいほど直線とデータの距離が近い
データは既知の値でパラメータのみ未知
$$MSE_{\rm train}=\frac{1}{n_{\rm train}}\sum_{k=1}^{n_{\rm train}}\Big(\hat{y_k}-y_k\Big)^2$$
最小二乗法
学習データの平均二乗誤差を最小とするパラメータを探索
$w$に対して微分したものが0となる$w$の点を求める。学習データの平均二乗誤差の最小化は、その勾配が0になる点を求めれば良い
$$\frac{\partial}{\partial w}MSE_{\rm train}=0$$
1-3.線形回帰ハンズオン(住宅価格予想)
2.非線形回帰モデル
複雑な非線形構造を内在する現象に対して、非線形回帰モデリングを実施
・データの構造を線形で捉えられる場合は限られる
・非線形な構造を捉えられる仕組みが必要
2-1.基底展開法
・回帰関数として、基底関数と呼ばれる既知の非線形関数とパラメータベクトルの線型結合を使用
・未知パラメータは線形回帰モデルと同様に最小2乗法や最尤法により推定
$$y_k=f(x_k)+\epsilon_k \qquad y_i=w_0+\sum_{k=1}^m w_k\phi_k(x_k)+\epsilon_k$$
よく使われる基底関数
多項式関数
$$\phi_k(x)=x^k$$
ガウス型基底関数
$$\phi_k(x)=\exp \Bigg(\frac{(x-\mu_k)^2}{2h_k}\Bigg)$$
スプライン関数/ Bスプライン関数
2-2.未学習(underfitting)と過学習(overfitting)
学習データに対して、十分小さな誤差が得られないモデル→未学習
(対策)モデルの表現力が低いため、表現力の高いモデルを利用する
小さな誤差は得られたけど、テスト集合誤差との差が大きいモデル→過学習
・(対策1) 学習データの数を増やす
・(対策2) 不要な基底関数(変数)を削除して表現力を抑止
・(対策3) 正則化法を利用して表現力を抑止
正則化項(罰則項)
無い▶最小2乗推定量
L2ノルムを利用▶Ridge推定量
$$R(w)=\sqrt{\sum_{k=1}^m w_k^2}=\sqrt{w_1^2+w_2^2+w_3^2+\cdots +w_m^2}$$
L1ノルムを利用▶Lasso推定量
$$R(w)=\sum_{k=1}^m|w_k|=|w_1|+|w_2|+|w_3|+\cdots +|w_m|$$
正則化パラータの役割
小さく▶制約面が大きく
大きく▶制約面が小さく
ホールドアウト法
有限のデータを学習用とテスト用の2つに分割し、「予測精度」や「誤り率」を推定する為に使用。
学習用を多くすればテスト用が減り学習精度は良くなるが、性能評価の精度は悪くなる。
逆にテスト用を多くすれば学習用が減少するので、学習そのものの精度が悪くなることになる。
手元にデータが大量にある場合を除いて、良い性能評価を与えないという欠点がある。
交差検証(クロスバリデーション)
データをいくつかのブロックに分割し、1つのブロックを検証データ、他を学習データとする。
学習データでモデルを学習させ、検証データで各モデルの精度を計測する、ということを分割数だけ繰り返す。
各々で得られた精度の平均(CV値)をそれぞれ算出する。
最もCV値が小さいものを採用する。
グリッドサーチ
全てのチューニングパラメータの組み合わせで評価値を算出
最も良い評価値を持つチューニングパラメータを持つ組み合わせを、「いいモデルのパラメータ」として採用
2-3. 非線形回帰のハンズオン
3.ロジスティック回帰
3-1.分類問題
ロジスティック回帰は分類問題の際に扱うモデルである。
3-2.分類で扱うデータ
入力:説明変数
$m$次元のベクトル
$$x=(x_1,x_2,x_3,\cdots,x_m)^T\in\mathbb{R^m}$$
出力:目的変数
離散値$y\in${0,1}
タイタニックデータ、IRISデータなど
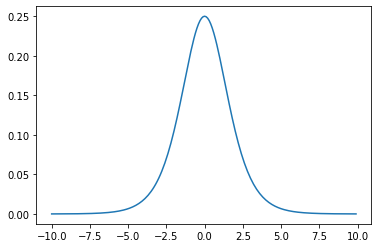
3-3. シグモイド関数
・入力は実数・出力は必ず0~1の値
・(クラス1に分類される)確率を表現
・単調増加関数$\sigma(x)$
3-3-1.パラメータが変わるとシグモイド関数の形が変わる
・aを増加させると,x=0付近での曲線の勾配が増加
・aを極めて大きくすると,単位ステップ関数(x<0でf(x)=0,x>0でf(x)=1となるような関数)に近づく。
・バイアス変化は段差の位置
$$\sigma(x)=\frac{1}{1+\exp(-ax)}=\frac{1}{1+e^{-ax}}$$

3-3-2.シグモイド関数の性質
・シグモイド関数の微分は、シグモイド関数自身で表現することが可能
・尤度関数の微分を行う際にこの事実を利用すると計算が容易
$$\sigma^{\prime}(x)=a\sigma(x)\big(1-\sigma(x) \big)$$
証明
\begin{eqnarray}
\sigma^{\prime}(x)&=&\bigg(\frac{1}{1+e^{-ax}}\bigg)^{\prime}\\
&=&\frac{-\big(-ae^{-ax}\big)}{(1+e^{-ax})^2}\\
&=&a\times\frac{1}{1+e^{-ax}}\times \frac{e^{-ax}}{1+e^{-ax}}\\
&=&a\times\frac{1}{1+e^{-ax}}\times \bigg(1-\frac{1}{1+e^{-ax}} \bigg)\\
&=&a\sigma (x)\Big(1- \sigma (x)\Big)
\end{eqnarray}
3-3-3.線形結合した値をシグモイド関数に与えることで$y=1$となる確率が出力
・データの線形結合を計算
・シグモイド関数に入力▶出力が確率に対応
・[表記] i番目データを与えた時のシグモイド関数の出力をi番目のデータがY=1になる確率とする求めたい値
$$P(Y=1|x)=\sigma(w_0+w_1x_1+w_2x_2+w_3x_3+\cdots+w_mx_m)$$
3-4.最尤推定
・元のデータである$x$、$y$を生成するに至る尤もらしいパラメータを探す推定方法
・尤度関数を最大化させる未知のパラメータを探す
・様々な確率分布があるが、ロジスティック回帰モデルではベルヌーイ分布を利用する
3-5.尤度関数
データを固定し、パラメータを変化させる
尤度関数を最大化するようなパラメータを選ぶ推定方法を最尤推定という
1回の試行で$y=y_1$となる確率
$$p(y)=p^y(1-p)^{1-y}$$
$n$回の試行で同時に、$y_1,y_2,y_3,\cdots,y_n$が起こる確率
\begin{eqnarray}
P(y_1,y_2,y_3,\cdots,y_n ;p)&=&\prod_{k=1}^np^{y_k}(1-p)^{1-y_k} \\
&=&\prod_{k=1}^n \Big(\sigma(w^Tx_k) \Big)^{y_k}\Big(1-\sigma(w^Tx_k)\Big)^{1-y_k} \\
&=& L(w)
\end{eqnarray}
3-6.対数尤度関数
尤度関数は式が積の形になっているので、対数を取り和の形に直すと計算が楽になる
対数尤度関数が最大になる点と尤度関数が最大になる点は同じとなる。
\begin{eqnarray}
-\log L(w)&=&-\log L(w_1,w_2,w_3,\cdots,w_m)\\
&=&-\Big(y_1\log y_1+\cdots+y_m\log y_m+(1-y_1)\log (1-y_1)+\cdots+ (1-y_m)\log (1-y_m)+\Big)\\
&=&-\sum_{k=1}^m\Big(y_k\log y_k+(1-y_k)\log(1-y_k) \Big)
\end{eqnarray}
対数尤度関数を微分して0になる点を求めることができないため、勾配降下法を使って逐次求める。
3-7.勾配降下法
反復学習によりパラメータを逐次的に更新するアプローチの一つ
対数尤度関数をパラメータで微分して0になる値を求める必要があるのだが、解析的にこの値を求めることは困難であるため、勾配降下法を用いる。
$$w^{k+1}=w^k-\eta\sum_{i=1}^n(y_i-p_i)x_i$$
データを全て使うため大量のメモリが必要になる。
計算時間が多くなる問題がある。
最適解ではなく局所最適解に収束する可能性がある。
3-8. 確率的勾配降下法
データを一つずつランダムに(「確率的」に)選んでパラメータを更新
$$w^{k+1}=w^k-\eta(y_i-p_i)x_i$$
勾配降下法でパラメータを1回更新するのと同じ計算量でパラメータをn回更新できるので効率よく最適な解を探索可能
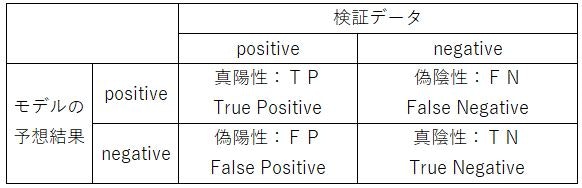
3-9. 混合行列
1.真陽性:TP(True Positive) ⇒ 正しくPositiveと判別した数
2.偽陽性:FP(False Positive) ⇒ 間違えてPositiveと判別した数
3.真陰性:TN(True Negative) ⇒ 正しくNegativeと判別した数
4.偽陰性;FN(False Negative) ⇒ 間違えてNegativeと判別した数
3-9-1. 正解率(Accuracy)
全データ($TP+FN+FP+TN$)のうち、正しく判別した($TP+TN$)確率
$$\frac{TP+TN}{TP+FN+FP+TN}$$
3-9-2. 再現率(Recall)
Positiveなデータ($TP+FN$)から、Positiveと予想($TP$)できる確率
$$\frac{TP}{TP+FN}$$
3-9-3. 適合率(Precision)
モデルがPositiveと予想したデータ$TP+FP$から、Positiveと予想($TP$)できる確率
$$\frac{TP}{TP+FP}=P$$
3-9-4. F値(F score)
再現率(Recall)と適合率(Precision)の調和平均
$$\frac{2}{\frac{1}{Recall}+\frac{1}{Precision}}=\frac{2(Precision)(Recall)}{Recall+Precision}$$
3-10.ロジスティック回帰モデルハンズオン
4.主成分分析
多変量データの持つ構造をより少数個の指標に圧縮
変量の個数を減らすことに伴う、情報の損失はなるべく小さくしたい
少数変数を利用した分析や可視化(2・3次元の場合)が実現可能
学習データ
$$x_i=(x_{i1},x_{i2},x_{i3},\cdots,x_{im})\in\mathbb{R^m}$$
平均(ベクトル)
$$\bar{x}=\frac{1}{n}\sum_{i=1}^n x_i$$
データ行列
$$\bar{X}=\Big(x_1-\bar{x},x_2-\bar{x},x_3-\bar{x},\cdots x_n-\bar{x}, \big)^T$$
分散共分散行列
$$Var(\bar{X})=\frac{1}{n}\bar{X}^T\bar{X} $$
線形変換後のベクトル
$$s_j=(s_{1j},s_{2j},s_{3j},\cdots,s_{nj})^{T}=\bar{X}a_j\qquad a_j\in\mathbb{R^m}$$
$j$ は射影軸のインデックス
4-1. ラグランジュ関数(目的関数・制約条件)
目的関数
$$\arg\max_{a\in\mathbb{R^m}} a_j^T Var(\bar{X}) a_j$$
制約条件は
$$a_j^Ta_j=1$$
制約条件付の最適化問題
⇒ ラグランジュ関数を最大にする係数ベクトル(微分して0になる点)を探索
4-2. ラグランジュ関数
$$E(a_j)=a_j^T Var(\bar{X}) a_j -\lambda \left(a_j^Ta_j-1\right)$$
ラグランジュ関数の両辺を微分して、係数ベクトル(微分して0になる点)を探す
$$\frac{\partial E(a_j)}{\partial a_j}=2Var (\bar{X})a_j-2\lambda a_j \quad (=0)$$
両辺2で割って、移行すると
$$Var (\bar{X})a_j=\lambda a_j$$
射影先の分散は固有値と一致する
$$Var (s_1)=a_1^TVar (\bar{X})a_1 =\lambda_1 a_1^Ta_1=\lambda_1$$
4-3. 寄与率
第$k$主成分の分散の全分散に対する割合(第$k$主成分が持つ情報量の割合)のことを寄与率$c_k$という
$$c_k=\frac{\lambda_k}{\displaystyle\sum_{i=1}^m\lambda_i}=\frac{\lambda_k}{\lambda_1+\lambda_2+\lambda_3+\cdots+\lambda_k +\cdots+\lambda_m}$$
4-4. 累積寄与率
第1から第$k$主成分まで圧縮した際の情報損失量の割合のことを累積寄与率$r_k$という。
$$c_k=\frac{\displaystyle\sum_{j=1}^k\lambda_j}{\displaystyle\sum_{i=1}^m\lambda_i}=\frac{\lambda_1+\lambda_2+\lambda_3+\cdots+\lambda_k }{\lambda_1+\lambda_2+\lambda_3+\cdots+\lambda_k +\cdots+\lambda_m}$$
乳がん検査データを利用しロジスティック回帰モデルを作成
主成分を利用し2次元空間上に次元圧縮
4-5.PCAハンズオン
5.アルゴリズム
5-1. k近傍法
教師あり学習の1つ。分類問題のための機械学習手法
最近傍のデータを$k$個取り、それらが最も多く属するクラスに識別する。
$k$を変化させると結果も変わる
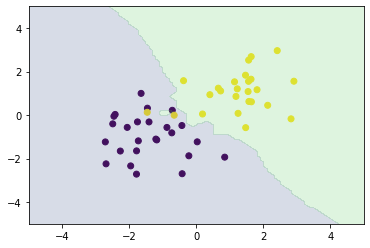
$k$を大きくすると決定境界は滑らかになる
5-2.k近傍法のハンズオン
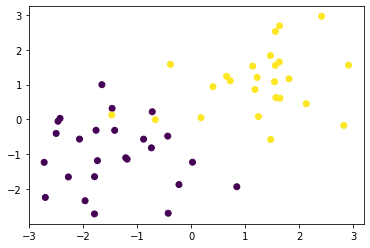
課題:人口データと分類結果をプロット
モジュールのインポート
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
訓練データの生成
def gen_data():
x0 = np.random.normal(size=50).reshape(-1, 2) - 1
x1 = np.random.normal(size=50).reshape(-1, 2) + 1.
x_train = np.concatenate([x0, x1])
y_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
return x_train, y_train
X_train, ys_train = gen_data()
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)
matplotlib.collections.PathCollection at 0x7f9ed90f2b38
# 距離の計算
def distance(x1, x2):
return np.sum((x1 - x2)**2, axis=1)
def knc_predict(n_neighbors, x_train, y_train, X_test):
y_pred = np.empty(len(X_test), dtype=y_train.dtype)
for i, x in enumerate(X_test):
distances = distance(x, X_train)
nearest_index = distances.argsort()[:n_neighbors]
mode, _ = stats.mode(y_train[nearest_index])
y_pred[i] = mode
return y_pred
# 図
def plt_resut(x_train, y_train, y_pred):
xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
plt.contourf(xx0, xx1, y_pred.reshape(100, 100).astype(dtype=np.float), alpha=0.2, levels=np.linspace(0, 1, 3))
# ハイパーパラメータk=3
n_neighbors = 3
xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
X_test = np.array([xx0, xx1]).reshape(2, -1).T
# k近傍法
y_pred = knc_predict(n_neighbors, X_train, ys_train, X_test)
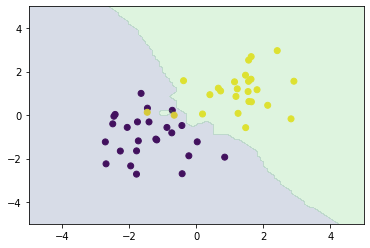
plt_resut(X_train, ys_train, y_pred)
numpyによる実装
xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T
from sklearn.neighbors import KNeighborsClassifier
knc = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X_train, ys_train)
plt_resut(X_train, ys_train, knc.predict(xx))
5-3. k-平均法(k-means)
$k$-平均法は教師なし学習の1つで、トップダウンでクラスタリングする機械学習の手法
$k$-平均法は教師なし学習、つまりラベルのないデータの分類方法です
与えられたデータを$k$個のクラスタリング(特徴が似ているグループ化)する。
クラスタリングのゴールは、同じクラスタ内のデータ点同士の距離が短くなるように、データを与えられた数のクラスタに分類していきます。具体的には、
$k$-平均法のアルゴリズム
1.各クラスタ中心の初期値を設定する
2.各データ点に対して、各クラスタ中心との距離を計算し、最も距離が近いクラスタを割り当てる
3.各クラスタの平均ベクトル(中心)を計算する
4.収束するまで2~3の処理を繰り返す