この記事でやること
過去に用いられたLogging Policy $\pi_b$によって収集されたデータを用いて、新たに導入を検討するPolicy $\pi_e$の性能推定に用いられるDM,IPS,DR推定量の期待値と分散を導出し、良し悪しを考察します。そして、最後にまとめとして「プラットフォーム全体で観測される報酬のオフ方策評価」におけるIPS推定量を独自に開発します。
Notation
| 記号 | 説明 | 補足 |
|---|---|---|
| $V(\pi_e)$ | 真の報酬関数 | |
| $\hat{V}(\pi_e)$ | $V(\pi_e)$の推定量 | |
| $u \in [1,n]$ | ユーザー集合 | |
| $x_u \in \mathcal{X}$ | ユーザー$u$の文脈 | |
| $a \in \mathcal{A}$ | アクション集合 | |
| $\pi_e$ | 評価方策(evaluation policy) | |
| $\pi_b$ | データ収集方策(behaivor policy) | |
| $\pi_{\cdot}(a|x_u)$ | ユーザー$u$の文脈$x_u$に対してアクション$a$を選択する確率 | $\sum_{a \in \mathcal{A}} \pi_{\cdot}(a|x_u) = 1$ |
オフ方策評価について
雑多なデータを用いて、何かしらのアルゴリズムの性能を評価したいという場面があります。例えば、推薦システムを例に挙げると、仮にアルゴリズムAからBに変えると、コンバージョンがどのくらい向上するのか?という施策の効果を測りたい状況が往々にしてあります。代表的な方法としては、A/Bテストなどのオンライン実験があります。しかし、A/Bテストは正しく効果を測れる一方でユーザー体験を損なう可能性があります。そこで、オフライン上で過去に収集されたデータを下に効果を測れるととても便利です。
ただ、過去に収集されたデータはほとんどの場合、母集団を代表していないという問題があります。その原因として過去の推薦方策の傾向がデータに反映されるというものやたまたまユーザーの目につきやすかったから観測されたなどがあります。オフ方策評価は、前者のバイアスに対処することで正しく効果を測る技術の総称になります。
これから登場する過去の方策$\pi_b$や評価方策$\pi_e$の分布はすでに得られているものとして話を進めていきます。例えば、オフ方策学習によって意思決定確率を直接学習されたものやバンディットや決定的な機械学習アルゴリズムを確率分布に変換したものなどを想像しています。
モチベーション
なぜ推定量$\hat{V}(\pi_e;\mathcal{D})$の期待値と分散をもとに評価をするのかいう理由についてですが、真の期待報酬$V(\pi_e)$の性能との"ズレ"をなるべく小さくしたいからです。
真の報酬関数
V(\pi_e) = \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \underbrace{\pi_e(a|x_u)}_{\text{既知}} \underbrace{q(x_u,a)}_{\text{未知}}
本来ならば、真の報酬$q(x_u,a)$(推薦システムの例だと、予め定義したユーザーがアイテムを"好む"という確率、クリック率、コンバージョン率など)が高いアクションに対してより高い$\pi_e(a|x_u)$という選択確率を割り振れているか評価をしたいわけです。"報酬"はたくさん欲しいはずなので。しかし、真の報酬$q(x_u,a)$なんてものは観測不可能で誰にも分かりません。なので、観測されたログデータ$\mathcal{D}$を用いて真の性能$V(\pi_e)$を推定する量、つまり推定量が必要であり"良い"推定量を開発したいのです。
"ズレ"は"バイアス"と"バリアンス"に分解できる
ここまで真の性能$V(\pi_e)$と推定量$\hat{V}(\pi_e; \mathcal{D})$の関係性を解説しました。ではこれらの"ズレ"を理論的にどう評価するのかについてですが、これらのMean Squared Error (MSE)を使うという方法があります。
\begin{align}
\text{MSE}(\hat{V}(\pi_e)) &= \mathbb{E}_{\mathcal{D}} \left[ \left( V(\pi_e) - \hat{V}(\pi_e; \mathcal{D}) \right)^2 \right] \\
&= \mathbb{E}_{\mathcal{D}} \left[ V(\pi_e)^2 - 2V(\pi_e)\hat{V}(\pi_e;\mathcal{D}) + \hat{V}(\pi_e;\mathcal{D})^2 \right] \\
&= V(\pi_e)^2 - 2V(\pi_e)\mathbb{E}_{\mathcal{D}}[\hat{V}(\pi_e;\mathcal{D})] + \mathbb{E}_{\mathcal{D}}[\hat{V}(\pi_e;\mathcal{D})^2] \\
&= V(\pi_e)^2 - 2V(\pi_e)\mathbb{E}_{\mathcal{D}}[\hat{V}(\pi_e;\mathcal{D})] + \mathbb{E}_{\mathcal{D}}[\hat{V}(\pi_e;\mathcal{D})]^2 + \mathbb{E}_{\mathcal{D}}[\hat{V}(\pi_e;\mathcal{D})^2] - \mathbb{E}_{\mathcal{D}}[\hat{V}(\pi_e;\mathcal{D})]^2 \\
&= \left(V(\pi_e) - \mathbb{E}_{\mathcal{D}}[\hat{V}(\pi_e;\mathcal{D})] \right)^2 + \mathbb{V}_{\mathcal{D}}[\hat{V}(\pi_e;\mathcal{D})] \\
&= \text{Bias}(\hat{V}(\pi_e;\mathcal{D})) + \mathbb{V}_{\mathcal{D}}[\hat{V}(\pi_e;\mathcal{D})] \\
\end{align}
統計的学習理論のバイアス、バリアンス分解と同じように$\text{MSE}(\hat{V}(\pi_e))$を展開して少しこねくり回すと、推定量$\hat{V}(\pi_e;\mathcal{D})$のバイアス(1項目)とバリアンス(2項目)に分解できます。
つまり、$\text{MSE}(\hat{V}(\pi_e))$を小さくするということは、推定量のバイアス$\text{Bias}(\hat{V}(\pi_e;\mathcal{D}))$とバリアンス$\mathbb{V}_{\mathcal{D}}[\hat{V}(\pi_e;\mathcal{D})]$を共に小さくするということと同義になります。
推定量に望みたい性質
MSEの意味で"良い"推定量を作るには推定量のバイアスとバリアンスを共に小さくできるようなものを作るればよいということを解説しましたが、具体的に推定量にはどのような性質を持っていてほしいのでしょうか。バイアス項とバリアンス項から考えます。
仮にバイアス項を0にできるならば、以下のような等式が成り立ちます。
\text{Bias}(\hat{V}(\pi_e;\mathcal{D})) = \left(V(\pi_e) - \mathbb{E}_{\mathcal{D}}[\hat{V}(\pi_e;\mathcal{D})] \right)^2 = 0
\therefore \mathbb{E}_{\mathcal{D}}[\hat{V}(\pi_e;\mathcal{D})] = V(\pi_e)
推定量の期待値が真の性能と等しくなる、つまり不偏性という性質があれば自ずとバイアスは0になります。不偏推定量を作りたいのであれば、推定量の期待値が真の性能と等しくなるように設計していけばよいということがわかります。
次にバリアンス項についてですが、まず一つの考察として、分散を減らすにはサンプル数が依存すると考えられます。サンプル数が少なければ推定値もばらつきやすくなるので。なので、サンプル数が増えると推定量の分散が小さくなってほしいという願望があります。ということで、2つ目に持っていてほしい推定量の性質として一致性が挙げられます。
\hat{V}(\pi_e; \mathcal{D}) \underset{|\mathcal{D}| \to \infty}{\to} V(\pi_e)
一致性の定義自体はサンプル数を増やすと推定量の性能が真の性能に確率的に一致するというもので、推定量の分散がサンプル数の増加に応じて小さくなることを保証するものではないのですが、前提として不偏推定量であれば、(基本的には)サンプル数に依存せずバイアスは0なので、加えて一致推定量であれば、サンプル数増加に応じて分散が小さくなると考えることができます。
まとめると、不偏性をもつような推定量を考えたうえで、複数の推定量の分散の式を眺めてどの分散が小さくなるのか判断していくという方針が基本になると考えられます。
観測データの生成仮定
ここからは観測データのみを用いて、真の性能$V(\pi_e)$をうまく近似できるような推定量を考えていきます。今回の記事では以下のようなデータが手元に得られていると仮定して話を進めていきます。
\begin{align}
\mathcal{D} &= \{(x_u, A_u, R_u) \}_{u=1}^{n} \\
(x_u, A_u, R_u) &\overset{\mathrm{i.i.d}}{\sim} \pi_b(\cdot|x_u)q(x_u,A_u) \\
\end{align}
観測データの説明
| 記号 | 説明 |
|---|---|
| $x_u$ | ユーザー$u$の文脈 |
| $A_u \sim \pi_b(\cdot|x_u)$ | データ収集方策$\pi_b$の確率分布に従う確率変数のアクション$A_u$ |
| $R_u(\in [0,1]) \sim q(x_u,A_u)$ | 真の報酬分布$q$に従う2値確率変数の報酬$R_u$ |
推薦するユーザーとその文脈はあらかじめ決まっていて、選択するアクションと報酬は確率的に決まるというデータの観測構造を置きました。推薦するユーザーは何かしらの条件で分析者によって絞り込まれることが現実的なのかなということで、推薦する$n$人のユーザーは決定的に決まるとします。
Direct Method (DM) 推定量
\hat{V}_{DM}(\pi_e; \mathcal{D}) = \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \pi_e(a|x_u) \hat{q}(x_u, a; \mathcal{D})
DM推定量は、未知の報酬期待値$q(x,a)$の代替として、観測データ$\mathcal{D}$からユーザーとアクションのペアの報酬を直接推定した$\hat{q}(x,a; \mathcal{D})$を用いることで新たな方策$\pi_e$の性能を評価します。
DM推定量の期待値
\begin{align}
\mathbb{E}_{\mathcal{D}} \left[ \hat{V}_{DM}(\pi_e;\mathcal{D}) \right] &= \mathbb{E}_{\mathcal{D}} \left[ \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \pi_e(a|x_u) \hat{q}(x_u, a; \mathcal{D}) \right] \\
&= \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \pi_e(a|x_u) \mathbb{E}_{\mathcal{D}}[ \hat{q}(x_u, a; \mathcal{D})] \\
&= \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \pi_e(a|x_u) (q(x_u,a) + \Delta (x_u,a))\\
\end{align}
ここで、$\mathbb{E}_{\mathcal{D}}[ \hat{q}(x_u, a; \mathcal{D})] = q(x_u,a) + \Delta (x_u,a)$と報酬の予測関数を推定量と考えて、その期待値を真の報酬関数$q(x_u,a)$と誤差項$\Delta (x_u,a)$の和で表せるという仮定を置きました。この誤差項$\Delta (x_u,a)$が$\forall x_u \in \mathcal{X},a \in \mathcal{A}: \Delta (x_u,a) = 0$でなければDM推定量はバイアスをもちます。
\left| \mathbb{E}_{\mathcal{D}} \left[ \hat{V}_{DM}(\pi_e;\mathcal{D}) \right] - V(\pi_e) \right| = \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \pi_e(x_u,a) \Delta(x_u, a)
汎化性能の意味で予測誤差を0にすることが不可能なことを考えるとこれから紹介するIPSとDR推定量よりもバイアスをもちます。
DM推定量の分散
\begin{align}
\mathbb{V}_{\mathcal{D}} \left[ \hat{V}_{DM}(\pi_e;\mathcal{D}) \right] &= \mathbb{V}_{\mathcal{D}} \left[ \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \pi_e(a|x_u) \hat{q}(x_u, a; \mathcal{D}) \right] \\
&= \frac{1}{n^2} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \pi_e(a|x_u)^2 \mathbb{V}_{\mathcal{D}}[ \hat{q}(x_u, a; \mathcal{D})] \\
&= \frac{1}{n^2} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \pi_e(a|x_u)^2 \hat{\sigma}^2(x_u,a) \\
\end{align}
独立同分布から得られたログデータ$\mathcal{D}$を用いて報酬の予測関数が得られたということで、DM推定量の分散も共分散をもたない形で表せるとしました。
Inverse Propensity Score (IPS) 推定量
\hat{V}_{IPS}\left( \pi_e;\mathcal{D} \right) = \frac{1}{n} \sum_{u=1}^{n} \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} R_u
但し、以下の仮定の下で。
\forall x_u \in \mathcal{X},A_u \in \mathcal{A}: \pi_e(A_u|x_u) > 0 \to \pi_b(A_u|x_u) > 0
IPS推定量は、データ収集方策$\pi_b$の選択確率を評価方策$\pi_e$の選択確率の分母に重み付けした形を取ります。但し、データ収集方策$\pi_b$の選択確率が0の場合推定量を定義できないため、上記の仮定の下、IPS推定量を定義できます。
なぜこのような形を取るのかですが、真の性能$V(\pi_e)$の不偏推定量を作るためです。
期待値の導出
\begin{align}
\mathbb{E}_{A,R} \left[\hat{V}_{IPS}\left( \pi_e;\mathcal{D} \right) \right] &= \mathbb{E}_{A,R} \left[ \frac{1}{n} \sum_{u=1}^{n} \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} R_u \right] \\
&= \frac{1}{n} \sum_{u=1}^{n} \mathbb{E}_{A,R} \left[ \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} R_u \right] \\
&= \frac{1}{n} \sum_{u=1}^{n} \mathbb{E}_{A} \left[ \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} \mathbb{E}_{R} \left[ R_u | A \right] \right] \\
&= \frac{1}{n} \sum_{u=1}^{n} \mathbb{E}_{A} \left[ \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} q(x_u, A_u) \right] \\
&= \frac{1}{n} \sum_{u=1}^{n} \sum_{a \in \mathcal{A}} \left[ \frac{\pi_e(a|x_u)}{\pi_b(a|x_u)} q(x_u, a) \right] \pi_b(a|x_u)
\qquad \scriptsize{\because \mathbb{E}_X[f(X)] = \sum_{x \in \mathcal{X}} f(x) \mathbb{P}(X=x) } \\
&= \frac{1}{n} \sum_{u=1}^{n} \sum_{a \in \mathcal{A}} \pi_e(a|x_u)q(x_u, a) \\
&= V(\pi_e)
\end{align}
IPS推定量$\hat{V}_{IPS}(\pi_e;\mathcal{D})$の期待値を計算すると真の性能$V(\pi_e)$と等しくなることから不偏推定量であることがわかります。
分散の導出
\begin{align}
\mathbb{V}_{A,R} \left[\hat{V}_{IPS}\left( \pi_e;\mathcal{D} \right) \right] &= \mathbb{V}_{A,R} \left[ \frac{1}{n} \sum_{u=1}^{n} \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} R_u \right] \\
&= \frac{1}{n^2} \sum_{u=1}^{n} \mathbb{V}_{A,R} \left[ \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} R_u \right]
\qquad \scriptsize{\substack{\because \mathbb{V}_{X}[aX]= a^2 \mathbb{V}_X[X], \\ \mathbb{V}_{X_1,...,X_n}[X_1 + \ldots + X_n] = \mathbb{V}_{X_1}[X_1] + \ldots + \mathbb{V}_{X_n}[X_n] (\text{独立同分布の仮定})}} \\
\end{align}
ここからは全分散の公式を用いて展開していきます。詳細は付録に加えました。
\mathbb{V}[Y] = \mathbb{E} \left[ \mathbb{V} \left[ Y | X \right] \right] + \mathbb{V} \left[ \mathbb{E} \left[ Y | X \right] \right]
$w(x_u,A_u) = \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)}$として、
\begin{align}
\mathbb{V}_{A,R} \left[ \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} R_u \right] &= \underbrace{\mathbb{E}_{A} \left[ \mathbb{V}_{R} \left[ w(x_u,A_u) R_u | A_u \right] \right]}_{(1)} + \underbrace{\mathbb{V}_{A} \left[ \mathbb{E}_{R} \left[ w(x_u,A_u) R_u | A_u \right] \right]}_{(2)} \\
\end{align}
\begin{align}
(1) &= \mathbb{E}_{A} \left[ w^2(x_u,A_u) \mathbb{V}_{R} \left[ R_u | A_u \right] \right] \\
&= \mathbb{E}_{A} \left[ w^2(x_u,A_u) \sigma^2(x_u,A_u) \right] \\[1cm]
(2) &= \mathbb{V}_{A} \left[ w(x_u,A_u) \mathbb{E}_{R} \left[ R_u | A_u \right] \right] \\
&= \mathbb{V}_{A} \left[ w(x_u,A_u) q(x_u,A_u) \right]
\end{align}
よってIPS推定量の分散は以下の通りになります。
\therefore \mathbb{V}_{A,R} \left[\hat{V}_{IPS}\left( \pi_e;\mathcal{D} \right) \right] = \frac{1}{n^2} \sum_{u=1}^{n} \mathbb{E}_{A} \left[ w^2(x_u,A_u) \sigma^2(x_u,A_u) \right] + \mathbb{V}_{A} \left[ w(x_u,A_u) q(x_u,A_u) \right]
データ収集方策$\pi_b$の選択確率が分母に残るので、評価方策$\pi_e$との確率分布が極端に異なる場合やデータ収集方策$\pi_e$の選択確率の分散が高い(決定的なアルゴリズムに近い)場合などに先のDM推定量よりも分散が大きい可能性が高いです。
Doubly Robust (DR) 推定量
\hat{V}_{DR}(\pi_e; \mathcal{D}) = \hat{V}_{DM}(\pi_e) + \frac{1}{n} \sum_{u=1}^n \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} (R_u - \hat{q}(x_u,A_u))
但し、以下の仮定の下で。
\forall x_u \in \mathcal{X},A_u \in \mathcal{A}: \pi_e(A_u|x_u) > 0 \to \pi_b(A_u|x_u) > 0
DM推定量とIPS推定量を上手いこと同時に使うことでIPS推定量の高分散問題に対処することを狙いとしたのがこのDR推定量です。
DR推定量がなぜこの形をしているのかですが、真の性能$V(\pi_e)$の不偏推定量を作りつつ、IPS推定量よりも分散を小さくすることを狙いとしているためです。
DR推定量の期待値
先ほどのDM推定量に用いた報酬の予測関数$\hat{q}(x_u,a; \mathcal{D})$を確率変数と仮定してDM推定量の期待値と分散を導出しましたが、DR推定量の期待値計算を容易にするため、今回は予測の報酬関数は実現値$\hat{q}(x_u,a)$とします($a$が確率変数$A$の実現値ならば、その意味で予測関数も確率変数$q(x_u,A_u)$ですが)。
\begin{align}
\mathbb{E}_{A,R} \left[\hat{V}_{DR}\left( \pi_e;\mathcal{D} \right) \right] &= \mathbb{E}_{A,R} \left[ \hat{V}_{DM}(\pi_e) + \frac{1}{n} \sum_{u=1}^n \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} (R_u - \hat{q}(x_u,A_u)) \right] \\
&= \hat{V}_{DM}(\pi_e) + \mathbb{E}_{A,R} \left[ \frac{1}{n} \sum_{u=1}^n \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} (R_u - \hat{q}(x_u,A_u)) \right] \\
&= \hat{V}_{DM}(\pi_e) + \frac{1}{n} \sum_{u=1}^n \mathbb{E}_{A} \left[ \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} (\mathbb{E}_{R}[R_u |A ] - \hat{q}(x_u,A_u)) \right] \\
&= \hat{V}_{DM}(\pi_e) + \frac{1}{n} \sum_{u=1}^n \mathbb{E}_{A} \left[ \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} (q(x_u,A_u) - \hat{q}(x_u,A_u)) \right] \\
&= \hat{V}_{DM}(\pi_e) + \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \left[ \frac{\pi_e(a|x_u)}{\pi_b(a|x_u)} (q(x_u,a) - \hat{q}(x_u,a)) \right] \pi_b(a|x_u) \\
&= \hat{V}_{DM}(\pi_e) + \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \pi_e(a|x_u)q(x_u,a) - \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \pi_e(a|x_u)\hat{q}(x_u,a) \\
&= \hat{V}_{DM}(\pi_e) + V(\pi_e) - \hat{V}_{DM}(\pi_e) \\
&= V(\pi_e)
\end{align}
ということで、報酬を直接予測した関数$\hat{q}(x_u,a)$の性能にかかわらずDR推定量はIPS推定量と同様に不偏推定量となります。
DR推定量の分散
\begin{align}
\mathbb{V}_{A,R} \left[\hat{V}_{DR}\left( \pi_e;\mathcal{D} \right) \right] &= \mathbb{V}_{A,R} \left[ \hat{V}_{DM}(\pi_e) + \frac{1}{n} \sum_{u=1}^n \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} (R_u - \hat{q}(x_u,A_u)) \right] \\
&= \mathbb{V}_{A,R} \left[ \frac{1}{n} \sum_{u=1}^n \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} (R_u - \hat{q}(x_u,A_u)) \right] \qquad \scriptsize{\because \mathbb{V}_{X}[a + X] = \mathbb{V}_{X}[X]} \\
&= \frac{1}{n^2} \sum_{u=1}^n \mathbb{V}_{A,R} \left[ \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} (R_u - \hat{q}(x_u,A_u)) \right] \qquad \scriptsize{\substack{\because \mathbb{V}_{X}[aX]= a^2 \mathbb{V}_X[X], \\ \mathbb{V}_{X_1,...,X_n}[X_1 + \ldots + X_n] = \mathbb{V}_{X_1}[X_1] + \ldots + \mathbb{V}_{X_n}[X_n] (\text{独立を同分布の仮定})}}
\end{align}
IPS推定量のときと同様に全分散の公式を用いると、 $w(x_u,A_u) = \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)}$として
\begin{align}
\mathbb{V}_{A,R} \left[ w(x_u,A_u) (R_u - \hat{q}(x_u,A_u)) \right] &= \underbrace{\mathbb{E}_{A} \left[ \mathbb{V}_{R} \left[ w(x_u,A_u) (R_u - \hat{q}(x_u,A_u)) |A \right] \right]}_{(1)} + \underbrace{\mathbb{V}_{A} \left[ \mathbb{E}_{R} \left[ w(x_u,A_u) (R_u - \hat{q}(x_u,A_u)) |A \right] \right]}_{(2)} \\
\end{align}
\begin{align}
(1) &= \mathbb{E}_{A} \left[ w^2(x_u,A_u) \mathbb{V}_{R} \left[R_u - \hat{q}(x_u,A_u) |A \right] \right] \\
&= \mathbb{E}_{A} \left[ w^2(x_u,A_u) \mathbb{V}_{R} \left[R_u|A \right] \right]
\qquad \scriptsize{\because \mathbb{V}_X [X - f(Y) | Y] = \mathbb{V}_X[X|Y] } \\
&= \mathbb{E}_{A} \left[ w^2(x_u,A_u) \sigma^2(x_u, A_u) \right] \\[1cm]
(2) &= \mathbb{V}_{A} \left[ w(x_u,A_u) \mathbb{E}_{R} \left[R_u - \hat{q}(x_u,A_u)|A \right] \right] \\
&= \mathbb{V}_{A} \left[ w(x_u,A_u) \mathbb{E}_{R} [R_u|A] - \hat{q}(x_u,A_u) \right]
\qquad \scriptsize{\because \mathbb{E}_X[f(X)|X] = f(X) } \\
&= \mathbb{V}_{A} \left[ w(x_u,A_u)(q(x_u,A_u) - \hat{q}(x_u,A_u)) \right] \\
\end{align}
よってDR推定量の分散は以下の通り。
\therefore \mathbb{V}_{A,R} \left[\hat{V}_{DR}\left( \pi_e;\mathcal{D} \right) \right] = \frac{1}{n^2} \sum_{u=1}^n \mathbb{E}_{A} \left[ w^2(x_u,A_u) \sigma^2(x_u, A_u) \right] + \mathbb{V}_{A} \left[ w(x_u,A_u)(q(x_u,A_u) - \hat{q}(x_u,A_u)) \right]
1項目の期待値はIPS推定量と同様のものですが、2項目は異なります。IPS推定量の分散では真の報酬期待値$q(x_u,A_u)$が分散の項に残りましたが、DR推定量の分散では、真の報酬期待値とDM推定量に用いられた報酬の予測値の誤差$q(x_u, A_u) - \hat{q}(x_u,A_u)$が残りました。これが意味することとしては、ある程度報酬の直接予測ができていれば、IPS推定量の分散よりもDR推定量のそれのほうが小さくなるということです。
推定量のバイアスとバリアンス 早見表
| 推定量 $\hat{V}(\pi_e; \mathcal{D})$ | バイアス $| V(\pi_e) - \mathbb{E}_{\mathcal{D}} [ \hat{V}(\pi_e; \mathcal{D}) ] |$ | バリアンス $\mathbb{V}_{\mathcal{D}}[\hat{V}(\pi_e; \mathcal{D})]$ |
|---|---|---|
| $\hat{V}_{DM}(\pi_e;\mathcal{D})$ | $\frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \pi_e(x_u,a) \Delta(x_u, a)$ | $\frac{1}{n^2} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \pi_e(a|x_u)^2 \hat{\sigma}^2(x_u,a)$ |
| $\hat{V}_{IPS}(\pi_e;\mathcal{D})$ | $0$ | $\frac{1}{n^2} \sum_{u=1}^{n} \mathbb{E}_{A}[ w^2(x_u,A_u) \sigma^2(x_u,A_u)] + \mathbb{V}_{A}[ w(x_u,A_u) q(x_u,A_u)]$ |
| $\hat{V}_{DR}(\pi_e;\mathcal{D})$ | $0$ | $\frac{1}{n^2} \sum_{u=1}^n \mathbb{E}_{A} [ w^2(x_u,A_u) \sigma^2(x_u, A_u)] + \mathbb{V}_{A}[ w(x_u,A_u)(q(x_u,A_u) - \hat{q}(x_u,A_u))]$ |
IPS推定量とDR推定量は共に不偏推定量かつ一致推定量であることが知られており、バリアンス項はデータを増やすと小さくなると考えられます。そして、DR推定量の分散は基本的にはIPS推定量よりも小さくなるので、理論上ではDR推定量の性能が最もよいと考えられます。
参考までに
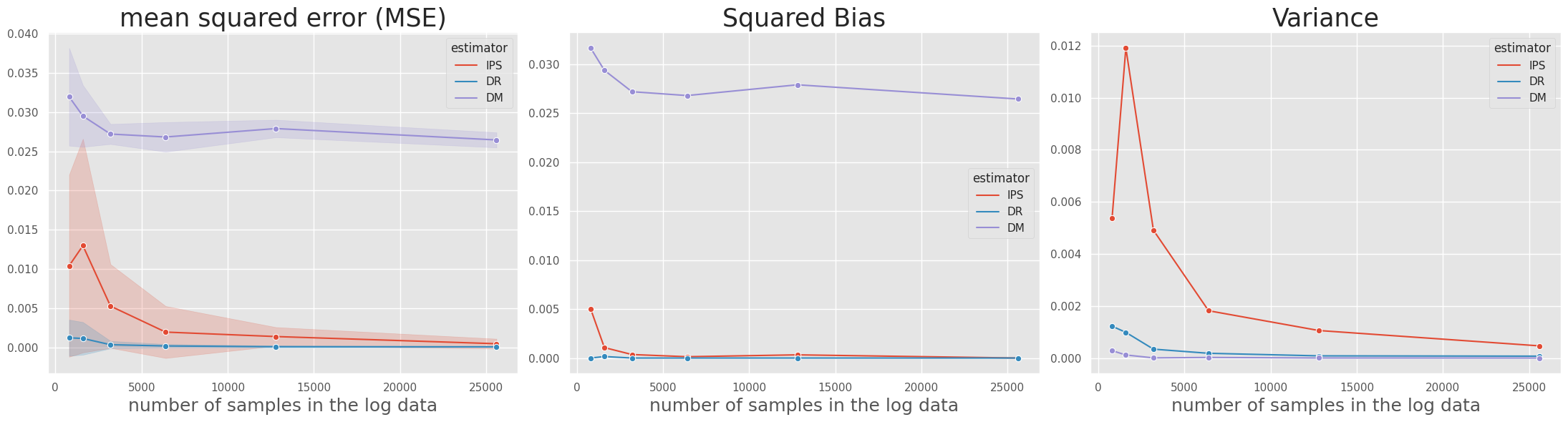
試しに[5]の実験コードを参考にOpen Bandit Pipelineを使用して各推定量のMSEを評価してみました。私の実験コードはこちらで確認できます。
おわりに
オフ方策評価における推定量の期待値と分散を分析する導入部分からそれらの導出までこの記事では行いました。真の性能と推定量の関係性の説明は[1][2]を参考に、期待値と分散の導出は[3][4]を参考に行いました。特に分散の導出までだいぶストイックにやったのですが、その意味としては真の性能と推定量は施策の目的によって決まるもので候補は無限に存在するからです。各会社、事業、目的などに応じたユニークな推定量の良し悪しを正しく判断するには、今回登場した基礎となる推定量の期待値と分散を導出することは良いトレーニングだと思いました。
"真の性能と推定量は無限に存在する"と言ってしまったので付録Cに「プラットフォーム全体で観測される報酬のオフ方策評価」を自分なりに考えてやってみました!ぜひ見てみてください。
参考文献
[1] 齋藤優太, 安井翔太. 施策デザインのための機械学習入門 : データ分析技術のビジネス活用における正しい考え方. 技術評論社,2021.
[2] Netflixを超えていけ!Contextual Banditアルゴリズムを徹底解説!(Part 2)
[3] Alekh Agarwal. Off-policy Evaluation and Learning. COMSE6998.001:Bandits and Reinforcement Learning,Fall2017.
[4] M. Dudík, J. Langford, and L. Li. Doubly robust policy evaluation and learning. Proceedings of the 28th International Conference on Machine Learning, Bellevue, WA, USA, 2011.
[5] Saito, Y. and Joachims, T. Off-policy evaluation for large action spaces via embeddings. In International Conference on Machine Learning, pp. 19089–19122. PMLR, 2022.
付録
A. 全分散の公式の導出
今回はユーザー文脈を確率変数とはしてませんが、ユーザー文脈が確率変数として条件部に複数の確率変数があっても同様に全分散の公式を扱えます。
\begin{align}
\mathbb{V}[X] &= \mathbb{E} \left[ \mathbb{V} \left[ X | Y_1,\ldots, Y_n \right] \right] + \mathbb{V} \left[ \mathbb{E} \left[ X | Y_1, \ldots, Y_n \right] \right] \\
&= \mathbb{E} \left[ \mathbb{E} \left[ X^2 | Y_1,\ldots, Y_n \right] - \mathbb{E} \left[ X | Y_1,\ldots, Y_n \right]^2 \right] + \mathbb{E} \left[ \mathbb{E} \left[ X | Y_1,\ldots, Y_n \right]^2 \right] - \mathbb{E} \left[ \mathbb{E} \left[ X | Y_1,\ldots, Y_n \right] \right]^2 \\
&= \mathbb{E} \left[ \mathbb{E} \left[ X^2 | Y_1,\ldots, Y_n \right] \right] - \mathbb{E} \left[ \mathbb{E} \left[ X | Y_1,\ldots, Y_n \right]^2\right] + \mathbb{E} \left[ \mathbb{E} \left[ X | Y_1,\ldots, Y_n \right]^2 \right] - \mathbb{E} \left[ \mathbb{E} \left[ X | Y_1,\ldots, Y_n \right] \right]^2 \\
&= \mathbb{E} \left[ \mathbb{E} \left[ X^2 | Y_1,\ldots, Y_n \right] \right] - \mathbb{E} \left[ \mathbb{E} \left[ X | Y_1,\ldots, Y_n \right] \right]^2 \\
&= \mathbb{E}[X^2] - \mathbb{E}[X]^2
\qquad \scriptsize{\because \mathbb{E}[\mathbb{E}[X|Y]] = \mathbb{E}[X]}\\
&= \mathbb{V}[X] \\
\end{align}
最後の変形には繰り返し期待値の法則を適用した。
B. 繰り返し期待値の導出
\begin{align}
\mathbb{E} \left[ \mathbb{E} \left[ X | Y_1, \ldots, Y_n \right] \right] &= \mathbb{E} \left[
\sum_{x} p(x|Y_1, \ldots, Y_n) x \right] \\
&= \sum_{y_1} \cdots \sum_{y_n} p(y_1, \ldots, y_n) \left[ \sum_{x} p(x|y_1,\ldots,y_n) x \right]
\qquad \scriptsize{\because \mathbb{E}[f(X,Y)] = \sum_{x} \sum_{y}p(x,y)f(x,y) } \\
&= \sum_{x} x \underbrace{ \sum_{y_1} \cdots \sum_{y_n} p(y_1,\ldots,y_n)p(x|y_1,\ldots,y_n)}_{\substack{\text{$p(x)$} \\
(\text{$y_1$から$y_n$までについて周辺化})}} \\
&= \sum_{x}xp(x) \\
&= \mathbb{E}[X]
\end{align}
C. プラットフォーム全体で観測される報酬のオフ方策評価
「施策デザイン本」[1]の5章をヒントに今回用いた基本推定量のIPS推定量を用いて、プラットフォーム全体で観測される報酬の最大化に取り組みます。よくある問題として、推薦経由のコンバージョンを最適化すると検索経由のコンバージョンが落ちてしまうというものがあります。その解決策の一つとして、コンバージョンしたデータがどの経路をたどってきたのかということをデータの観測構造に仮定することで、真の性能を近似した推定量を作ろうという方法があります。では、本来解きたい真の性能を以下に定義します。
V(\pi_e) = \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}}\pi_e(a|x_u) \left( q^{\text{rec}}(x_u,a) - q^{\text{other}}(x_u,a) \right)
ここで、推薦経由でコンバージョン(cv)する期待値を$q^{\text{rec}}(x_u,a)$として、推薦経由以外からコンバージョン(cv)する期待値を$q^{\text{other}}(x_u,a)$としました。つまり、推薦経由のcvを正しく評価するにはそのcvから推薦経由以外のcvを引いたものを真の報酬としてあげれば良さそうです。
データの観測構造
\begin{align}
\mathcal{D} &= \{ (x_u, A_u, R_{u}^{ctr}, R_{u}^{cvr}) \}_{u=1}^n \\
(x_u, A_u, R_{u}^{ctr}, R_{u}^{cvr}) &\overset{\mathrm{i.i.d}}{\sim} \pi_b(\cdot|x_u)p^{ctr}(x_u,A_u)q(x_u,A_u,R^{ctr}_u)
\end{align}
ここで、CTRとCVRの分布を以下のように定義しました。
\begin{align}
p^{ctr}(x_u,a) &= p(R_{u}^{ctr} = 1 | A_u = a) \\
&= \mathbb{E}_{R^{ctr}}[R_{u}^{ctr}|A = a] \\[1cm]
q(x_u, a, R_{u}^{ctr}) &=
\left\{
\begin{array}{l}
p(R_{u}^{cvr} = 1 | R_{u}^{ctr} = 1, A_u = a) = q^{rec}(x_u,a) \quad \text{if} \quad R_{u}^{ctr} = 1 \\
p(R_{u}^{cvr} = 1 | R_{u}^{ctr} = 0, A_u = a) = q^{other}(x_u,a) \quad \text{if} \quad R_{u}^{ctr} = 0
\end{array}
\right.
\end{align}
つまり、過去の推薦方策$\pi_b$がユーザー文脈$x_u$に対して、アクション$a$を選択して、クリックが発生すると$R_{u}^{ctr} = 1$となり、さらにコンバージョンが発生すると、$R_{u}^{cvr} = 1$という観測構造を"推薦経由でのコンバージョン"とします。
そして、推薦方策$\pi_b$がアクション$a$を選択したがクリックが発生しないと$R_{u}^{ctr} = 0$となるが、他の経路(例えば、検索など)からコンバージョンが発生すると$R_{u}^{cvr} = 1$という構造を"推薦経由以外でのコンバージョン"とします。
IPS推定量の定義
もう結論から、先に定義した真の性能$V(\pi_e)$に対するIPS推定量は以下のようになります。
\hat{V}_{IPS}(\pi_e; \mathcal{D}) = \frac{1}{n} \sum_{u=1}^n \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} \left( \frac{R_{u}^{cvr}R_{u}^{ctr}}{p^{ctr}(x_u, A_u)} - \frac{R_{u}^{cvr} (1 - R_{u}^{ctr})}{1 - p^{ctr}(x_u, A_u)} \right)
但し、以下の仮定の下で。
\forall x_u \in \mathcal{X},A_u \in \mathcal{A}: \pi_e(A_u|x_u) > 0 \to \pi_b(A_u|x_u) > 0
IPS推定量の期待値
期待値を計算して、真の性能$V(\pi_e)$と等しくなるのか確かめます。
\begin{align}
\mathbb{E}_{A,R^{ctr},R^{cvr}}[\hat{V}_{IPS}(\pi_e; \mathcal{D})] &= \mathbb{E}_{A,R^{ctr},R^{cvr}} \left[ \frac{1}{n} \sum_{u=1}^n \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} \left( \frac{R_{u}^{cvr}R_{u}^{ctr}}{p^{ctr}(x_u, A_u)} - \frac{R_{u}^{cvr} (1 - R_{u}^{ctr})}{1 - p^{ctr}(x_u, A_u)} \right) \right] \\
&= \frac{1}{n} \sum_{u=1}^n \mathbb{E}_{A,R^{ctr},R^{cvr}} \left[ \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} \left( \frac{R_{u}^{cvr}R_{u}^{ctr}}{p^{ctr}(x_u, A_u)} - \frac{R_{u}^{cvr} (1 - R_{u}^{ctr})}{1 - p^{ctr}(x_u, A_u)} \right) \right] \\
&= \frac{1}{n} \sum_{u=1}^n \mathbb{E}_{A} \left[ \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} \left( \frac{\mathbb{E}_{R^{ctr},R^{cvr}}[R_{u}^{cvr}R_{u}^{ctr}|A]}{p^{ctr}(x_u, A_u)} - \frac{\mathbb{E}_{R^{ctr},R^{cvr}}[R_{u}^{cvr}(1 - R_{u}^{ctr})|A]}{1 - p^{ctr}(x_u, A_u)} \right) \right] \\
&= \frac{1}{n} \sum_{u=1}^n \mathbb{E}_{A} \left[ \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} \left( \frac{q^{rec}(x_u,A_u)p^{ctr}(x_u, A_u)}{p^{ctr}(x_u, A_u)} - \frac{q^{other}(x_u,A_u)(1-p^{ctr}(x_u, A_u))}{1 - p^{ctr}(x_u, A_u)} \right) \right] \\
&= \frac{1}{n} \sum_{u=1}^n \mathbb{E}_{A} \left[ \frac{\pi_e(A_u|x_u)}{\pi_b(A_u|x_u)} \left(q^{rec}(x_u,A_u) - q^{other}(x_u,A_u) \right) \right] \\
&= \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}} \left[ \frac{\pi_e(a|x_u)}{\pi_b(a|x_u)} \left(q^{rec}(x_u,a) - q^{other}(x_u,a) \right) \right] \pi_b(a|x_u) \\
&= \frac{1}{n} \sum_{u=1}^n \sum_{a \in \mathcal{A}}\pi_e(a|x_u) \left( q^{\text{rec}}(x_u,a) - q^{\text{other}}(x_u,a) \right) \\
&= V(\pi_e)
\end{align}
$\mathbb{E}_{R^{ctr},R^{cvr}}[R_{u}^{cvr}R_{u}^{ctr}|A]$の計算についてですが、$R_{u}^{ctr}$と$R_{u}^{cvr}$は明らかに$A$の条件付き独立ではないということと、期待値計算にベイズの定理を使うと求まります。
\begin{align}
\mathbb{E}_{R^{ctr},R^{cvr}}[R_{u}^{cvr}R_{u}^{ctr}|A] &= \sum_{r^{cvr}=0}^1 \sum_{r^{ctr}=0}^1 r^{cvr}r^{ctr} p(R_{u}^{cvr} = r^{cvr}, R_{u}^{ctr} = r^{ctr} | A) \\
&= p(R_{u}^{cvr} = 1, R_{u}^{ctr} = 1 | A) \\
&= p(R_{u}^{cvr} = 1 | R_{u}^{ctr} = 1, A) p(R_{u}^{ctr} = 1 | A) \\
&= q^{rec}(x_u,A)p^{ctr}(x_u,A)
\end{align}
$\mathbb{E}_{R^{ctr},R^{cvr}}[R_{u}^{cvr}(1 - R_{u}^{ctr})|A]$についても同様です。
\begin{align}
\mathbb{E}_{R^{ctr},R^{cvr}}[R_{u}^{cvr}R_{u}^{ctr}|A] &= \sum_{r^{cvr}=0}^1 \sum_{r^{ctr}=0}^1 r^{cvr}(1-r^{ctr}) p(R_{u}^{cvr} = r^{cvr}, R_{u}^{ctr} = r^{ctr} | A) \\
&= p(R_{u}^{cvr} = 1, R_{u}^{ctr} = 0 | A) \\
&= p(R_{u}^{cvr} = 1 | R_{u}^{ctr} = 0, A) p(R_{u}^{ctr} = 0 | A) \\
&= q^{other}(x_u,A)(1-p^{ctr}(x_u,A))
\end{align}
ということで、IPS推定量は不偏推定量となります。DR推定量も同様にできそうです。