はじめに
seabornでは色んなデータセットが公開されているので、その中にあるpenguinsのデータセットを使って重回帰分析をPythonで行ってみます。
事前準備
必要なライブラリ、データのインポート
import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import statsmodels.api as sm
from statsmodels.formula.api import ols
penguins = sns.load_dataset("penguins", cache=False)
データの確認
最初の数行を表示して中身を確認してみます。
print(penguins.head(10))
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex
0 Adelie Torgersen 39.1 18.7 181.0 3750.0 Male
1 Adelie Torgersen 39.5 17.4 186.0 3800.0 Female
2 Adelie Torgersen 40.3 18.0 195.0 3250.0 Female
3 Adelie Torgersen NaN NaN NaN NaN NaN
4 Adelie Torgersen 36.7 19.3 193.0 3450.0 Female
5 Adelie Torgersen 39.3 20.6 190.0 3650.0 Male
6 Adelie Torgersen 38.9 17.8 181.0 3625.0 Female
7 Adelie Torgersen 39.2 19.6 195.0 4675.0 Male
8 Adelie Torgersen 34.1 18.1 193.0 3475.0 NaN
9 Adelie Torgersen 42.0 20.2 190.0 4250.0 NaN
データの準備
欠損値の処理
前節よりデータセットの最初の数行より利用可能な列と値がわかり、欠損しているデータがあることも確認されました。よって欠損データがデータセット全体に含まれる割合を確認します。
print(penguins.shape)
(344, 7)
欠損の合計値を確認します。
print(penguins.isnull().sum())
species 0
island 0
bill_length_mm 2
bill_depth_mm 2
flipper_length_mm 2
body_mass_g 2
sex 11
dtype: int64
欠損データの割合が5%未満と少量であるので「欠損行を削除する」か「平均値、中央値などによる補完」を選択するのが一般的です。
本来であればどうやって欠損値を補完するかを真剣に議論して決めないといけないのですが、ここではお勉強も兼ねて平均値、中央値、前の値で埋める、と様々なパターンで埋めておこうと思います。
# 平均値
penguins['bill_length_mm'] = penguins['bill_length_mm'].fillna(penguins['bill_length_mm'].mean())
penguins['bill_depth_mm'] = penguins['bill_depth_mm'].fillna(penguins['bill_depth_mm'].mean())
# 中央値
penguins['flipper_length_mm'] = penguins['flipper_length_mm'].fillna(penguins['flipper_length_mm'].median())
penguins['body_mass_g'] = penguins['body_mass_g'].fillna(penguins['body_mass_g'].median())
# 前方向埋め
penguins['sex'] = penguins['sex'].fillna(method = 'ffill')
print(penguins.head(10))
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex
0 Adelie Torgersen 39.10000 18.70000 181.0 3750.0 Male
1 Adelie Torgersen 39.50000 17.40000 186.0 3800.0 Female
2 Adelie Torgersen 40.30000 18.00000 195.0 3250.0 Female
3 Adelie Torgersen 43.92193 17.15117 197.0 4050.0 Female
4 Adelie Torgersen 36.70000 19.30000 193.0 3450.0 Female
5 Adelie Torgersen 39.30000 20.60000 190.0 3650.0 Male
6 Adelie Torgersen 38.90000 17.80000 181.0 3625.0 Female
7 Adelie Torgersen 39.20000 19.60000 195.0 4675.0 Male
8 Adelie Torgersen 34.10000 18.10000 193.0 3475.0 Male
9 Adelie Torgersen 42.00000 20.20000 190.0 4250.0 Male
モデルの構築
変数の選択
モデルを実装する前に変数の間に線形関係があるかどうかを確認します。散布図を作成するのが一番簡単なので、それでチェックします。
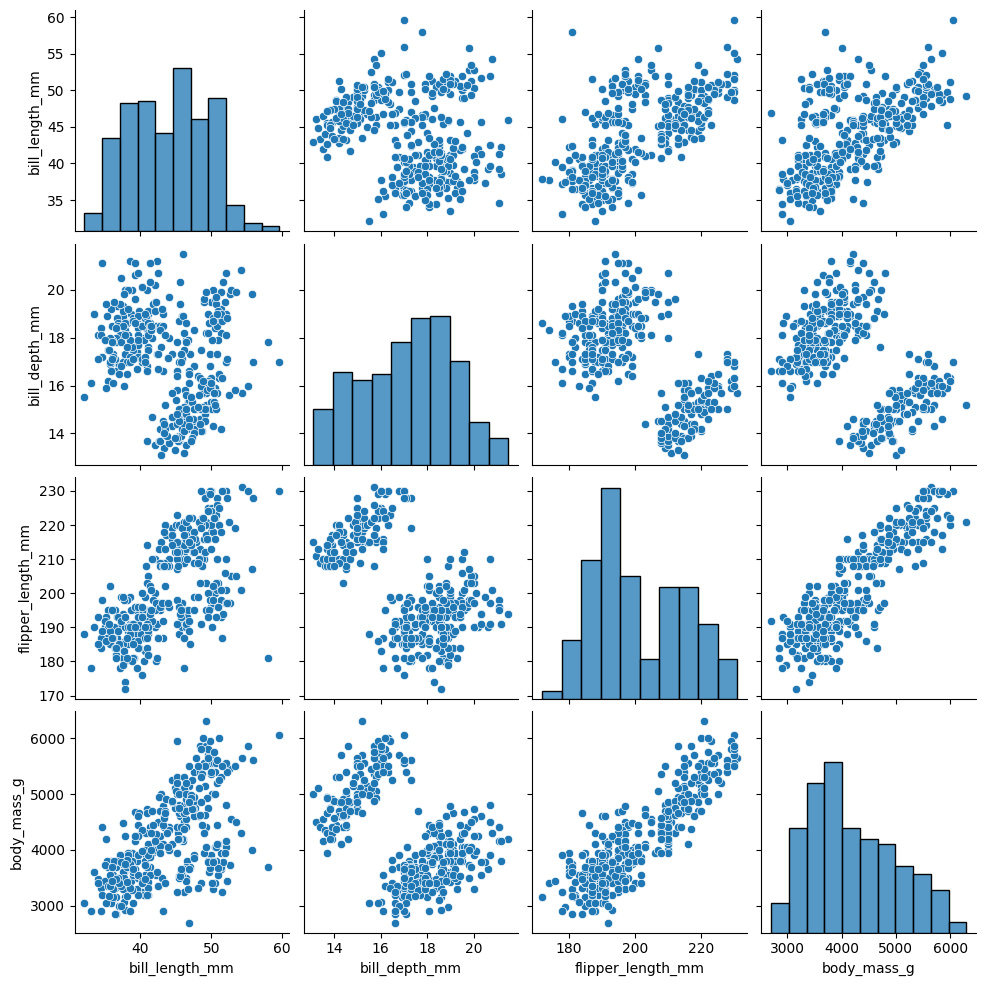
pg = sns.pairplot(penguins)
pg.savefig('C:/data/seaborn_pairplot_default.png')
出力例：
散布図より以下の変数の間には線形性がありそうということが確認出来ます。
- bill length (mm) と flipper length (mm)
- bill length (mm) と body mass (g)
- flipper length (mm) と body mass (g)
また、対角線上のヒストグラムよりflipper length (mm)を除く、bill length (mm)、bill_depth_mm、body mass (g)は正規分布してそう、ということがわかります。これは、残差が正規分布している可能性が高そうであることを示しています。
重回帰分析の式を考える
このデータではbody_mass_gを目的変数とし、1つの連続変数(bill length (mm)) と、2つのカテゴリ変数(sex と species) を説明変数とします。bill length (mm)を$x_1$、sexを$x_2$、speciesを$x_3$とするとき、次のような重回帰式を考えます。
y =
β_0 + β_1x_1 + β_2x_2 + β_3x_3
これを通常の最小二乗推定のOLSで実装していきます。
補足
body mass (g) を目的変数とすると、上記散布図よりflipper length (mm)が一番相関関係が強そうですが、この変数を用いると
[2] The condition number is large, 6.52e+03. This might indicate that there are strong multicollinearity or other numerical problems.
（条件数は 6.52e+03 と大きいです。これは、強い多重共線性またはその他の数値の問題があることを示す可能性があります。）
と多重共線性が疑われる、またそうでなくとも値が正規分布に従っていない為、ここではbill length (mm)を説明変数として選択しました。
OLSによる分析
# OLS関数の式の引数を定義する。
# カテゴリ変数であるsex, speciesについては C() を使用する。
ols_formula = "body_mass_g ~ bill_length_mm + C(gender) + C(species)"
# ホールドアウト検証で作成したトレーニングデータを準備する。
ols_data = pd.concat([X_train, y_train], axis = 1)
# 式とデータよりOLSオブジェクトを作成。
OLS = ols(formula = ols_formula, data = ols_data)
# 線形回帰モデルをデータにあてはめる。
model = OLS.fit()
# 結果の出力
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: body_mass_g R-squared: 0.840
Model: OLS Adj. R-squared: 0.838
Method: Least Squares F-statistic: 443.9
Date: Mon, 06 Jan 2025 Prob (F-statistic): 2.53e-133
Time: 19:47:21 Log-Likelihood: -2472.1
No. Observations: 344 AIC: 4954.
Df Residuals: 339 BIC: 4973.
Df Model: 4
Covariance Type: nonrobust
===========================================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------------------
Intercept 1749.2883 271.481 6.443 0.000 1215.288 2283.288
C(sex)[T.Male] 481.3681 43.095 11.170 0.000 396.601 566.135
C(species)[T.Chinstrap] -403.4945 86.998 -4.638 0.000 -574.619 -232.370
C(species)[T.Gentoo] 979.2004 73.837 13.262 0.000 833.964 1124.437
bill_length_mm 43.9575 7.282 6.037 0.000 29.635 58.280
==============================================================================
Omnibus: 1.022 Durbin-Watson: 2.236
Prob(Omnibus): 0.600 Jarque-Bera (JB): 0.816
Skew: -0.105 Prob(JB): 0.665
Kurtosis: 3.111 Cond. No. 735.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
誤差に関するモデルの仮定を確認
残差の独立性
OLS Regression Results を確認するとDurbin-Watsonの値が2.236であることが確認出来ます。これより、自己相関はナシと判断、独立性は満たされた、と言えます。（ダービン=ワトソン比の値が2前後のときは相関なしと判断されます）
残差の正規性
得られた結果に対して残差の正規性の仮定を確認します。
ヒストグラムによる確認
残差のヒストグラムを作成し確認するのが簡便です。
# モデルの残差の取得
residuals = model.resid
# 残差のヒストグラムを作成。
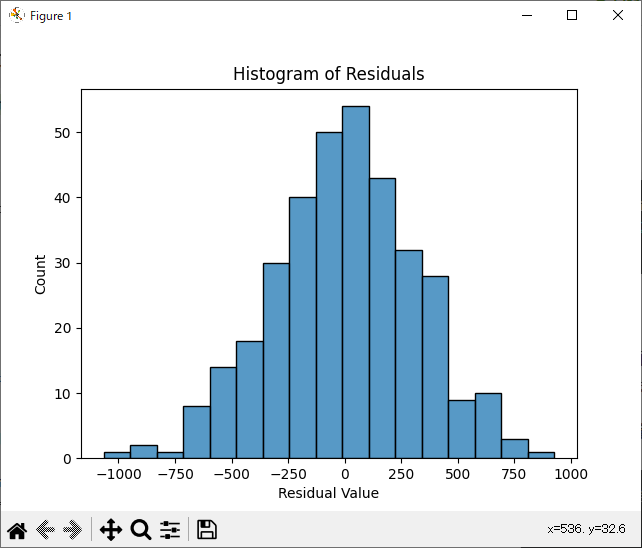
fig = sns.histplot(residuals)
fig.set_xlabel("Residual Value")
fig.set_title("Histogram of Residuals")
plt.show()
出力例：
図より残差の分布はほぼ正規分布となっており、これにより、正規性の仮定が満たされている可能性が高い、と言えます。
正規Q-Qプロットによる確認
もしくはQ-Qプロットでも正規性を確認することが出来ます。
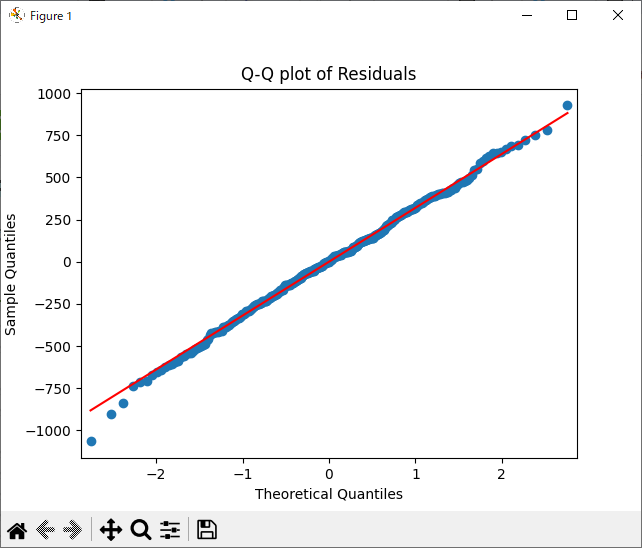
sm.qqplot(residuals, line='s')
plt.title("Q-Q plot of Residuals")
plt.show()
出力例：
各点が右肩上がりの直線に従っています。これより、正規性の仮定が満たされていることが確認できます。
残差の等分散性
散布図による確認
等分散性の仮定を確認するには散布図を用いるのが簡便です。
# モデルから適合値を取得
fitted_values = model.predict(ols_data)
# 散布図の作成
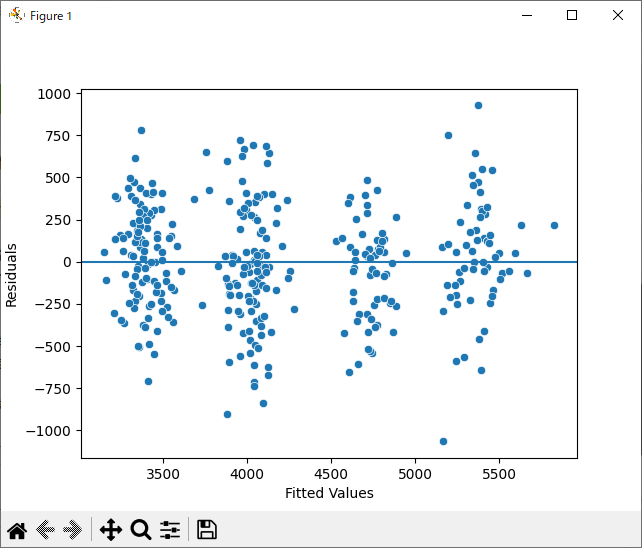
fig = sns.scatterplot(x=fitted_values, y=residuals)
fig.axhline(0)
fig.set_xlabel("Fitted Values")
fig.set_ylabel("Residuals")
plt.show()
出力例：
散布図では、明確なパターンに従っていないように見えます。ただし、Fitted Valueが3250, 4000, 4750, 5250あたりに群が出来ているので、念の為、ホワイト検定を行っておきます。
ホワイト検定
ホワイト検定では帰無仮説が棄却されると、分散不均一の存在が示唆されます。
from statsmodels.stats.diagnostic import het_white
# ホワイト検定を実行
white_test_stat, white_test_p_value, _, _ = het_white(model.resid, model.model.exog)
print("White test statistic:", white_test_stat)
print("White test p-value:", white_test_p_value)
White test statistic: 17.124601635385062
White test p-value: 0.07165193222097335
p値が0.07であり、有意水準5％では帰無仮説を棄却できないようです。よって、等分散性の仮定は満たされているようです。
モデルの評価と解釈
決定係数（R-Squared）と自由度調整済み決定係数（Adj. R-squared）
まずは、モデルによって説明されるbody_mass_gの変動の量を示す決定係数（R-Squared）の値を確認します。決定係数（R-Squared）の値が0.840という高い数値となっており、これはbody_mass_gの変動の84%がモデルによって説明できることを意味します。
自由度調整済み決定係数（Adj. R-squared）についても、0.838と、決定係数とほぼ変わらない為、問題なし（元のデータに対する当てはまりが良いモデルである）と判断できます。
表の下半分には、モデルによって推定されたベータ係数と、それに対応する 95% 信頼区間およびp値が表示されています。全ての変数$x_1$, $x_2$, $x_3$に対するP>|t|のp値を確認すると0.05未満であるため、すべての変数$x_1$, $x_2$, $x_3$が統計的に有意であると判断できます。
各変数xに対する係数βの解釈
次に、各変数xの係数βを解釈していきます。
C(sex)（性別）
C(sex)[T.Male]の変数名より Male = 1, Female = 0 としてエンコードされていることがわかります。つまり、メスのペンギンが基準です。他のすべての変数が同じであれば、オスのペンギンの体重はメスのペンギンの体重より約481.37グラム重いと推測できます。
C(species)（種）
C(species)[T.Chinstrap], C(species)[T.Gentoo]の2つの変数名より、Adelieが基準である、とわかります。したがって、種以外は同じ特徴を持つアデリーペンギンとヒゲペンギンを比較すると、ヒゲペンギンの体重はアデリーペンギンより約403.49gほど軽いと予想されます。種以外は同じ特徴を持つアデリーペンギンとジェンツーペンギンを比較すると、ジェンツーペンギンの体重はアデリーペンギンより約979.20gほど重いと推測できます。
bill_length_mm（くちばしの長さ）
最後に、bill_length_mm（くちばしの長さ）は連続変数であるため、くちばしが1mm長いことを除いて同じ特徴を持つ2匹のペンギンを比較すると、くちばしが長いペンギンの体重は、くちばしが短いペンギンより約43.96gほど重いと推測できます。
以上。