この記事はなんなのか
この記事は、学校の授業で論理ゲートから全加算器までを習ったものの頭がついていかなかった筆者が、
『Pythonでコードにしながら考えたらわかるんちゃうか?』
という発想のもと、普段お世話になりまくっている割にブラックボックスと化しているCPUについて少しでも造詣を深めよう(そしてついでにコーディングにも慣れよう)というものです。
今回の記事では論理ゲートから実装し、4bit全加算器を作っていきます。
そもそもPython自体に論理演算子はあるのですが、ご愛敬ということで....。
筆者は今年まともにプログラミングを始めた人間ですので、その辺ご理解宜しくお願いします。
CPUとは
Central Processing Unit(中央演算装置)の略省で、コンピューターの心臓ともいえる場所です。自作でPCを組む時に購入するCPUは小さな正方形のチップですが、内部は様々な役割を持った部分に分かれています。

(出典:Wikipedia,Author:Eric Gaba)
CPUの内部構造
CPU内部は大きく演算部と制御部に分けられます。
演算部
- 演算レジスタ
- ALU(演算装置)
上記の2つの構造に分けられます。レジスタというのはメモリのことで、演算レジスタは計算に使う数値を一時的に入れておく場所になります。ALUはCPUの中で計算をする部分で、算術演算や論理演算を行う専用の回路を持っています。現在のCPUは内部に様々な回路を有するようですが、今回の記事では簡単のために加算に限定し、後々さらに掘り下げていきます。
制御部
- 命令レジスタ
- 命令デコーダ
- 制御信号生成回路
- プログラムカウンタ
- アドレス制御回路
- 汎用レジスタ
命令レジスタはRAMに入っている命令が一時的にはいります。命令デコーダ(解読器)は命令レジスタのデータを受けて解読し、制御信号生成回路につたえます。制御信号生成回路は演算部の他、プログラムカウンタやアドレス制御回路にも制御信号を送るようです。プログラムカウンタはCPUがメモリ(RAM)の何番地の命令を読み込んでいるかを記憶しています。アドレス制御回路はプログラムカウンタのデータを受け、次に読み込むRAMの番地を指定します。汎用レジスタは様々な用途に使われるレジスタです。
ブール代数
上記に挙げたデジタル回路は0と1しか制御することができません。そこで、19世紀にイギリスのジョージ・ブールの考案した、論理の真偽を演算で処理できるブール代数を用います。(ブール代数の発表が1854年、エニアックの完成が1946年なので歴史的にはブール代数によってデジタル回路が出来たと考えた方が良いのかもしれません。知らんけど。)CPUの論理回路はブール代数で実現されます。以下では基本的な論理演算を組み合わせることで4bit全加算器をつくります。これは、先述のALUにあたります。
基本的な論理演算
CPUを考える上で知る必要があるのは基本的な3つの論理演算(AND, OR, NOT)です。それぞれ見ていきましょう。実際には以下の論理演算は複数の与えられた命題に対して成立するものですが、今回はCPUがメインなので2つの値(0と1)の関係として説明します。
AND(Logical Conjunction,論理積)
与えられた二つの値が共に1である時に1を返します。
| 入力1 | 入力2 | 出力 |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
def conjunction(a,b):
c=a*b
return c
論理積らしさを感じるコードにしてみました。
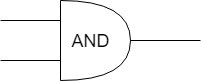
論理回路図ではこのような記号で書かれます。(中のANDの文字は私が暗記するために勝手にいれました。ふつうはこんな文字ないです。)
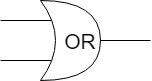
OR(Logical Disjunction, 論理和)
与えられた二つの値のうちどちらか一方が1なら1を返します。
| 入力1 | 入力2 | 出力 |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
def disjunction(a,b):
if a+b >= 1:
return 0
else:
return 1
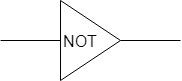
NOT(Negation,否定)
1と0を入れ替えて出力します。インバータとも呼ばれます。
| 入力1 | 出力 |
|---|---|
| 1 | 0 |
| 0 | 1 |
def inverter(a):
if a is 0:
return 1
else:
return 0
コンピューターを動かすためのすべての論理回路は上記の3つを組み合わせることで実現できます。
これらを用いて加算器を作るためのパーツを作っていきましょう。
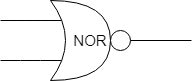
NOR(Not OR,否定論理和)
与えられた値がどちらも0であれば1を返します。これはORの結果を否定したと考えることができます。
| 入力1 | 入力2 | 出力 |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
def NOR(a,b):
c=disjuction(a,b)
d=inverter(c)
return d
XOR(eXclusive-OR,排他的論理和)
二つの値が一致しないときに1となります。
| 入力1 | 入力2 | 出力 |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
def XOR(a,b):
c=conjunction(a,b)
d=NOR(a,b)
e=NOR(c,d)
return e
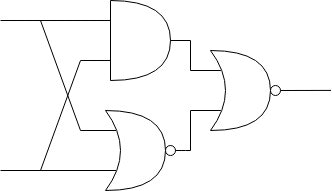
このように、ANDとNORだけで作ることができます。
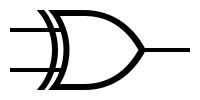
(出典:Wikipedia)
またこのような1つの記号でも表されます。
これで加算器を作る準備ができました。半加算器から全加算器、複数bitの加算器をつくっていきます。
加算器の具体的な仕組みなどはこちら(コンピューターの原理基礎:足し算を行う基本論理回路をシミュレーターで理解しよう!)のサイト様がわかりやすいと思います。
半加算器
半加算器は2進数で一桁の足し算を実行します。0+0,1+0,1+1を計算することができます。
これまでの論理演算とは異なり、桁上がりができるようになっています。この上がった桁をキャリーといいます。
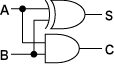
(出典:Wikipedia)
def half_adder(a,b):
adder_sum=XOR(a,b)
carry=conjunction(a,b)
return adder_sum,carry
全加算器
半加算器2つとORを組み合わせることで、下の桁からの繰り上がりを考慮した加算ができるようになります。
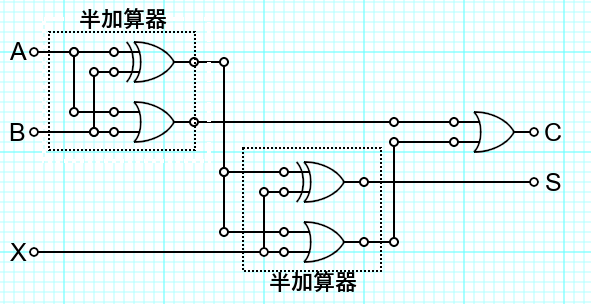
(Made byLogic Gate Simulator,Modified by 筆者)
上の図ではA,Bが入力、Xが下の桁からの繰り上がりになります。Cが次の桁への繰り上がりで、Sが同じ桁での加算の結果です。
def full_adder(a,b,x):
half_adder_sum,carry=half_adder(a,b)
full_adder_sum,ha_carry2=half_adder(half_adder_sum,x)
full_adder_carry=disjunction(carry,ha_carry2)
return full_adder_sum, full_adder_carry
戻り値が複数ある関数を使うとき、変数をコンマで定義してやればええんですね。。
4bit加算器
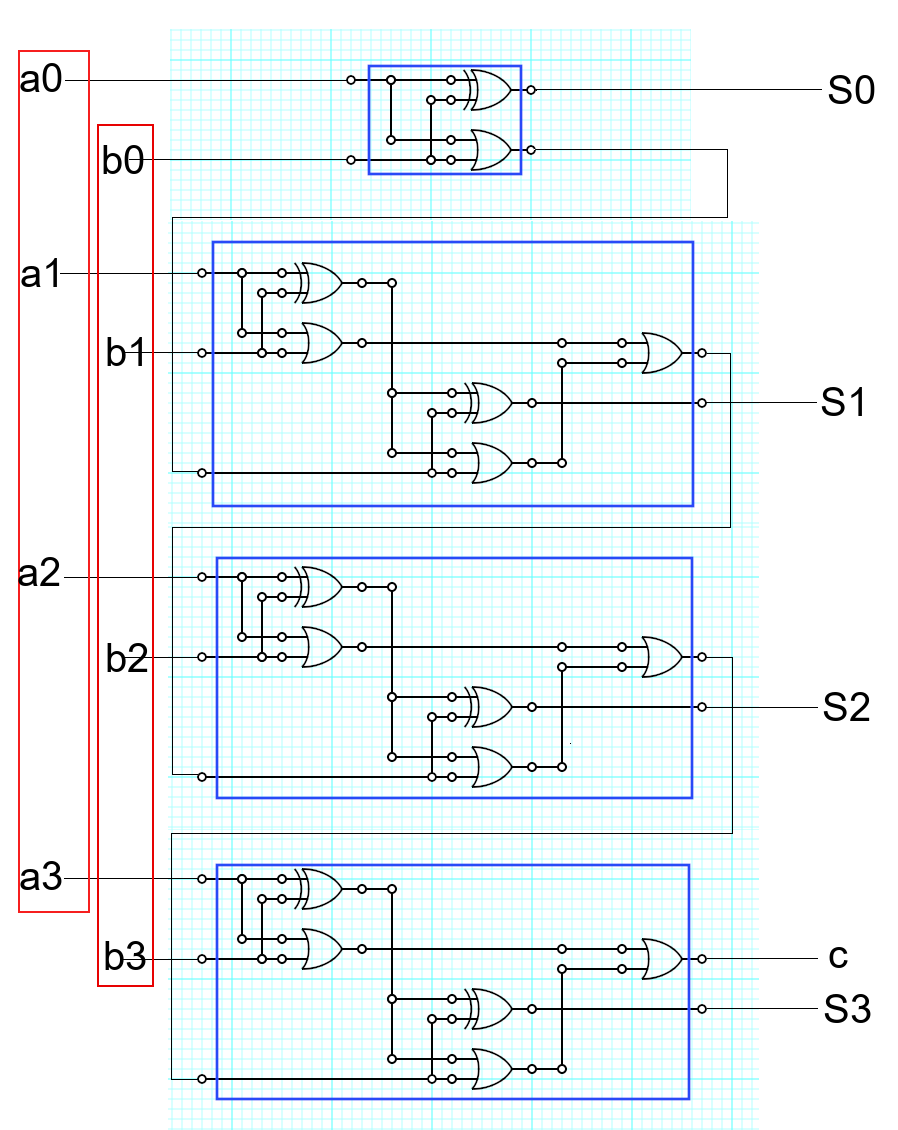
半加算器1つと全加算器3つを組み合わせることで4bit加算器ができます。合計が31以下の足し算を行うことができます。4bit同士の2入力で最大5bitまでの出力をします。下の図ではS0が1の位、S3が4の位で、cが最大の桁となります。
def adder_4bit(a0,a1,a2,a3,b0,b1,b2,b3):
ha_sum,ha_carry=half_adder(a0,b0)
fa_sum1,fa_carry1=full_adder(a1,b1,ha_carry)
fa_sum2,fa_carry2=full_adder(a2,b2,fa_carry1)
fa_sum3,fa_carry3=full_adder(a3,b3,fa_carry2)
sum_4bit=(ha_sum,fa_sum1,fa_sum2,fa_sum3,fa_carry3)
return sum_4bit
というわけで4bitの全加算器が完成しました。今回は図の作成でめちゃくちゃ時間を食ってしまいましたが、次回はレジスタをDフリップフロップからつくっていこうと思います。(出来んのかしらんけど。)