要約
- 画像の特徴べクトルとは、単に特徴を並べただけのもの。
- ベクトルは数学的に定量的に比較できる
- 適切な特徴を組み合わせれば画像を比較したり、物を認識したりできる
- 嬉しい!
背景
わけあって画像認識をかじったことがあるのですが、文献に当たり前のように出てくる「特徴ベクトル」と言う単語が分からずに開いてはそっ閉じする日々が続いてきました。イメージを掴むのに苦労したので、私なりの解釈をまとめておきます。ただ、難しい理論はわからないので、飽くまで「ざっくりこういう発想のものだ」という説明をしたいと思います。読み物だと思って読んでもらえれば。
特徴とは
そもそもの話ですが、ある画像や画素がどんなものであるかを説明するための材料のことを「特徴」といいます。
例えば、分かりやすいところでは次のようなものは特徴といえるでしょう。
- 色:青い、赤いなど
- 明るさ:明るい、暗いなど
- 形:四角い、丸いなど
- 色の分布(ヒストグラム)
- 空間周波数
- 穴の数
- 面積
- 周辺長
これらはわかりやすさのために挙げただけなので「こんなのも特徴と言えるよね」程度に思ってください。実際の特徴抽出器は普通ここに挙げたものよりもっと難しい特徴を使います。たとえばエッジ検出とか画像の勾配とかそういうものです。
また、実際には「面積」や「穴の数」のような「面」の特徴でなく、「画素」に対する特徴とする多いです(特徴点という)。例えば「この点は角の部分である」とか、「この点は線の上にある」とかいう具合です。そして「画像Aのこの点と同じものが画像Bには含まれているだろうか」というような使い方をします。このあたりは以下の記事が分かりやすいです。
画像処理の数式を見て石になった時のための、金の針(@icoxfog417)
https://qiita.com/icoxfog417/items/adbbf445d357c924b8fc
「じゃあその特徴とやらををどのようにして検出(抽出)するんだぜ?」というのはこの記事では触れません。というかそんな知識が私にありません。
特徴ベクトルとは
「値を並べたもの」を数学の世界ではベクトルと呼びます。そして、特徴ベクトルとは特徴を並べたものです。
以上です。
・・・・で終わっては乱暴でしょうか?wでも本当です。例えば、次のようなものも特徴が並んでいるので特徴ベクトルと呼ぶことが可能です。
色:赤
形:四角い
穴:1つ
面積:100
ちなみにこの特徴ベクトルは次の画像から抽出したものです1。

どのような特徴を並べるかは本当に様々で、それが画像処理アルゴリズムの肝となると言っても過言ではありません。かなり訳のわからん高度な処理の結果を並べて特徴ベクトルとすることが多く、ここで躓く人は多いでしょう。また、上で使っておいてなんですが、実際は数学的操作のしやすさの観点から「赤、青、黃」とか「四角、三角」のような列挙でなく、数値の羅列になる場合がほとんどです。
ベクトルは定量的に比較できるから嬉しい
で、ベクトルにしたところで何が嬉しいのかという話です。
ベクトルは数学の世界でそれはそれはもう深く深く研究されています。単なる値の羅列に対して様々な数学的操作を定量的(曖昧さなく)に行えます。それが嬉しいのです2。
数学的操作の一例が「比較」です。訳のわからん難しい数学的演算でベクトル同士の「近さ」を測ることができるのです。具体的にはノルム(ベクトルの大きさみたいなもの、絶対値)やコサイン類似度などといった指標が使われることがあります。
比較する例~どれが似てる?~
簡単な例として、次の画像でどれとどれが似ているかを判断する事を考えてみます。

※正方形のサイズは縦横300px、大きい円は直径300px、小さい円は直径50pxです
あなたは、どれとどれの画像が似ていると思いますか?なぜそう思いますか?似ているとはなんですか?
この問の答えは「定義による」です。そして「似ている」を曖昧さなく定義するために特徴ベクトルが必要なのです。
さて、今回は上の図形の色(R)、色(G)、色(B)、面積、周辺長を並べて特徴ベクトルとしましょう。
\begin{align}
図形1 &= (255, 0, 0, 88037, 1200)\\
図形2 &= (255, 0, 0, 43037, 942)\\
図形3 &= (0, 255, 0, 86075, 1200)
\end{align}
これらのベクトルの差分(の絶対値)が小さいほど似ていると定義します。早速計算してみましょう。忙しい人は太字だけ読んでください。
\begin{align}
図形1 - 図形2 &= (255- 255, 0-0, 0-0, 884037-43037, 1200-942)\\
&= (0, 0, 0, 45000, 258)\\
絶対値 &= \sqrt{0^2 + 0^2 + 0^2 + 45000^2 + 258^2}\\
&= \sqrt{2025066564}\\
&= {\bf 45000.7}
\end{align}
\begin{align}
図形1 - 図形3 &= (255-0, 0-255, 0-0, 884037-86075, 1200-1200)\\
&= (255, -255, 0, -43038, 0)\\
絶対値 &= \sqrt{255^2 + -255^2 + 0^2 + 1962^2 + 0^2}\\
&= \sqrt{3979494}\\
&= {\bf 1994.8}
\end{align}
\begin{align}
図形2 - 図形3 &= (255-0, 0-255,0-0, 43037-86075, 942-1200)\\
&= (255, -255, 0, -43038, -258)\\
絶対値 &= \sqrt{255^2 + -255^2 + 0^2 + -43038^2 + -258^2}\\
&= \sqrt{1852466058}\\
&= {\bf 43040.3}
\end{align}
この計算結果から、これらの図形の中では差分が1994.8と一番小さい図形1と図形3が似た図形だと判断することができます。この方法では色より形が重視されるようです。また、穴の数の違いは問題視されないようです。
この結果は「今回の定義ではこう判断できた」という話です。もちろん「色が近いこと=似ている」という考え方もあり得て、その場合はもっと違う特徴ベクトルを定義したり、色に重み付けをした演算を行うことになるでしょう。結局、繰り返しになりますが、特徴ベクトルとその演算をどう定義するかの問題です。そして、SURFやAKAZEといった既存のアルゴリズムを理解するということは特徴ベクトルとその演算がどう定義されているか理解することと同義です3。
このように、特徴ベクトルうまく定義すれば簡単な画像認識を行えることがわかります。更に応用すれば次のようなことも実現できそうです。
- この製品は規格より5mm大きいので不良品と判断しよう
- 制限速度が50km/hなので50km/hで自動運転をしよう
- 画像Aのこの点と画像Bのこの点は同じものだ。画像は連結してパノラマにできそうだ
特徴ベクトルが嬉しい理由、というか、どこでも必ず登場する理由がわかっていただけたかと思います。
拡大・縮小に強い特徴
しばしば「拡大・縮小に強い特徴」とか「拡大に対して不変」、「拡大(スケーリング)に対してロバスト」などという記載を目にします。これは画像を拡大・縮小しても特徴ベクトルの値があまり変わらないということを意味します。
これも初めて聞くと意味不明ですので、分かりやすい具体例を挙げましょう。拡大・縮小に弱い特徴の一つは面積です。面積は拡大・縮小を行うと明らかに変わってしまいます。同じ画像を同じものと認識できなくなるので拡大、縮小の可能性がある画像のマッチングをするのに面積を特徴にしてはいけません。
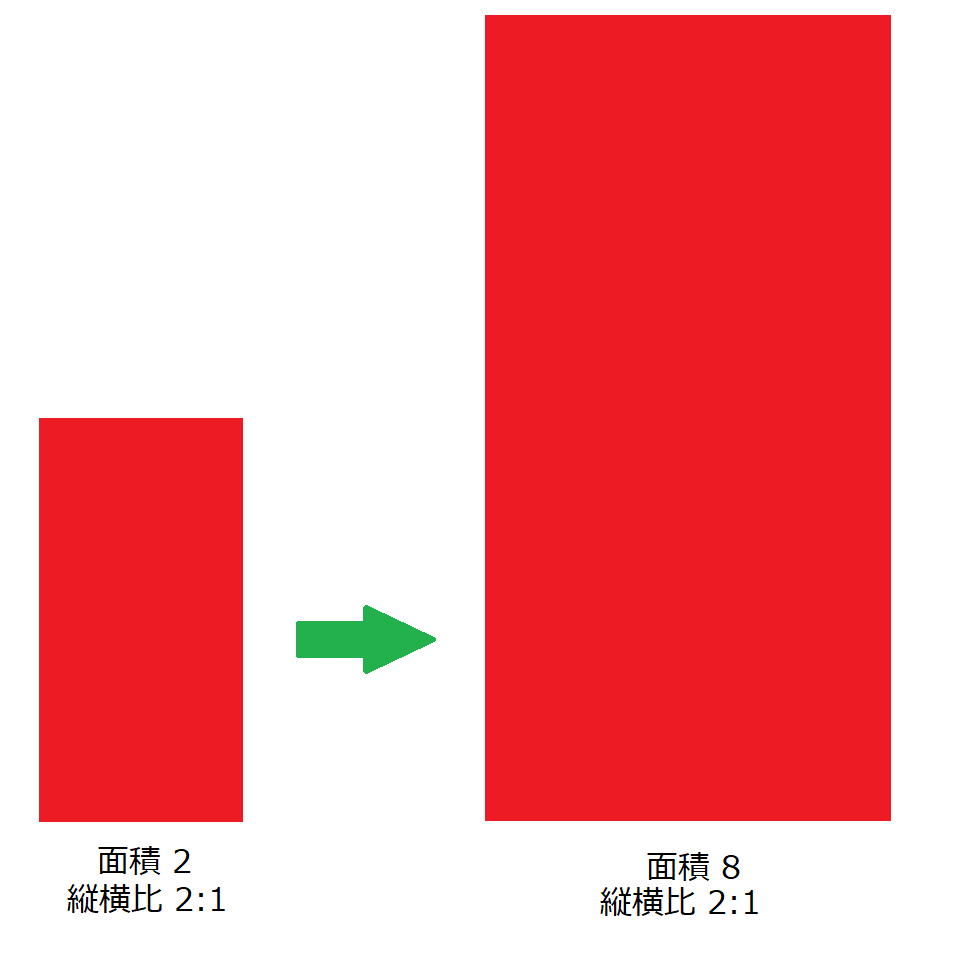
それに対して拡大・縮小に強い特徴は、例えば比率です。比率を使えば、画像を拡大・縮小しても値が変わることはないので「拡大・縮小に強い」と言えるのです。
回転に強い特徴
同様に、回転に強い特徴というものもあります。
回転に弱い特徴の例はずばり角度です。回転させたら角度が変わってしまうので、同じ画像だと認識できなくなります。
回転に強い特徴はかなり複雑な計算をしている事が多いので簡単な例を挙げるのは私には難しいのですが、強いて挙げるとすればやはり比率でしょうか4。
比率を用いれば回転していても特徴は変わりません。

その他の強い特徴
その他にも、明るさの変化に強い、ノイズに強いなど様々な〇〇に強い特徴があります。画像処理の用途によって特徴の特性を理解して使い分ける必要があります。大きさが変わったら別物だと扱う場合、拡大・縮小に強い特徴を使うのは向いていないかもしれません。
蛇足
ベクトルは矢印?
ところで、ベクトルと聞いて「矢印」を思い浮かべようとするは私だけでしょうか?しかし画像処理ではさぞ当たり前のように128次元ベクトルみたいなものが出てきます。3次元空間に生きている私にとって、4次元以上の矢印など想像しようがありません。少なくとも画像処理を考えるにあたってはベクトル=矢印の認識ではいけないようです。
どうしても視覚的に捉えたいのであればヒストグラムあるいはレーダーチャートを想像すると少しマシかも知れません。レーダーチャートを重ねて比較するイメージ5。
