はじめに
本記事では
対数変換とBox-Cox変換について解説しています。本記事は主に「機械学習のための特徴量エンジニアリング」を参考とさせて頂いておりますので、気になる方は是非チェックしてみてください。
また本記事の内容をより詳しくYouTubeで解説しているのでこちらも気になる方はチェックしてみてください。
※本記事で解説するプログラムは全てこちらにあります。
対数変換とは
対数変換は主に以下の目的で使用されます。
- 正規分布に従わせる
- 分散を減らす
対数関数は以下の図の様な関数でありxが[1,10]の範囲を[0,1]に写し、[10,100]の範囲を[1,2]に写すので、xの値が小さい場合は広い範囲に写され、xの値が大きい場合は狭い範囲に写されることが分かる。
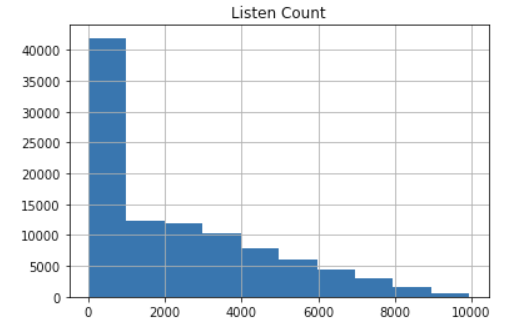
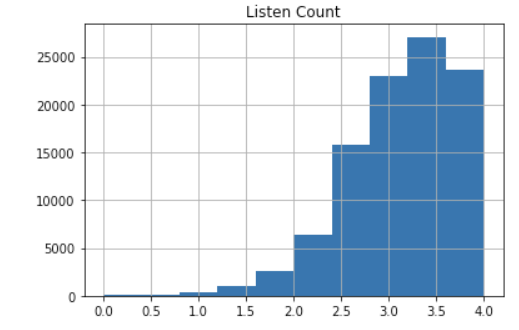
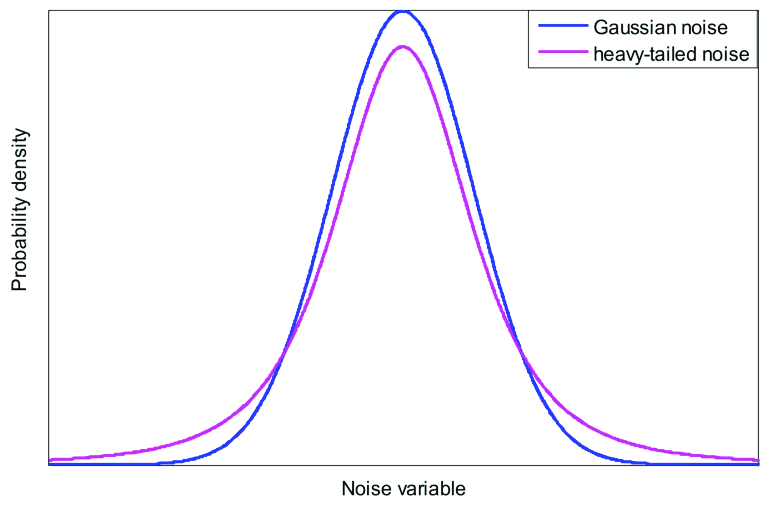
この対数変換を用いると、以下のような裾の重い分布の上側を圧縮し、下側を拡大して正規分布に近づけることができる。
多くの機械学習手法では母集団に特に仮定をおかないノンパラメトリックモデルが多いので正規分布に近づける必要はないのですが、統計母集団の分布を仮定しているパラメトリックモデルを使用する場合はデータの分布を正規分布にする必要があります。
また下記の様な分散の大きいデータに対して対数変換を用いることで、分散を減らすことができる。
対数変換適用前(分散: 5.0e+06)
対数変換適用後(分散: 0.332007)
対数変換適用のサンプルコード
import numpy as np
import pandas as pd
##乱数固定
np.random.seed(100)
data_array = []
for i in range(1, 10000):
max_num = i if i > 3000 else 1000
s = np.random.randint(0, max_num, 10)
data_array.extend(s)
data = pd.DataFrame({'Listen Count': data_array})
data_log = pd.DataFrame()
##0になるのを防ぐために1を足す
data_log['Listen Count'] = np.log10(data['Listen Count'] + 1)
Box-Cox変換とは
以下の式で定義できる変換
y=\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{x^\lambda - 1}{\lambda}~~~~~(if ~~ \lambda\neq0) \\
\log(x)~~~~~(if ~~ \lambda=0)
\end{array}
\right.
\end{eqnarray}
ある程度正規分布に従ったデータにしたいしてBox-Cox変換を用いることで、データを正規分布に従わせることができる。(※ただしデータが正の場合にのみ使用可能。)
この変換をグラフで表すと以下の図の様になります。
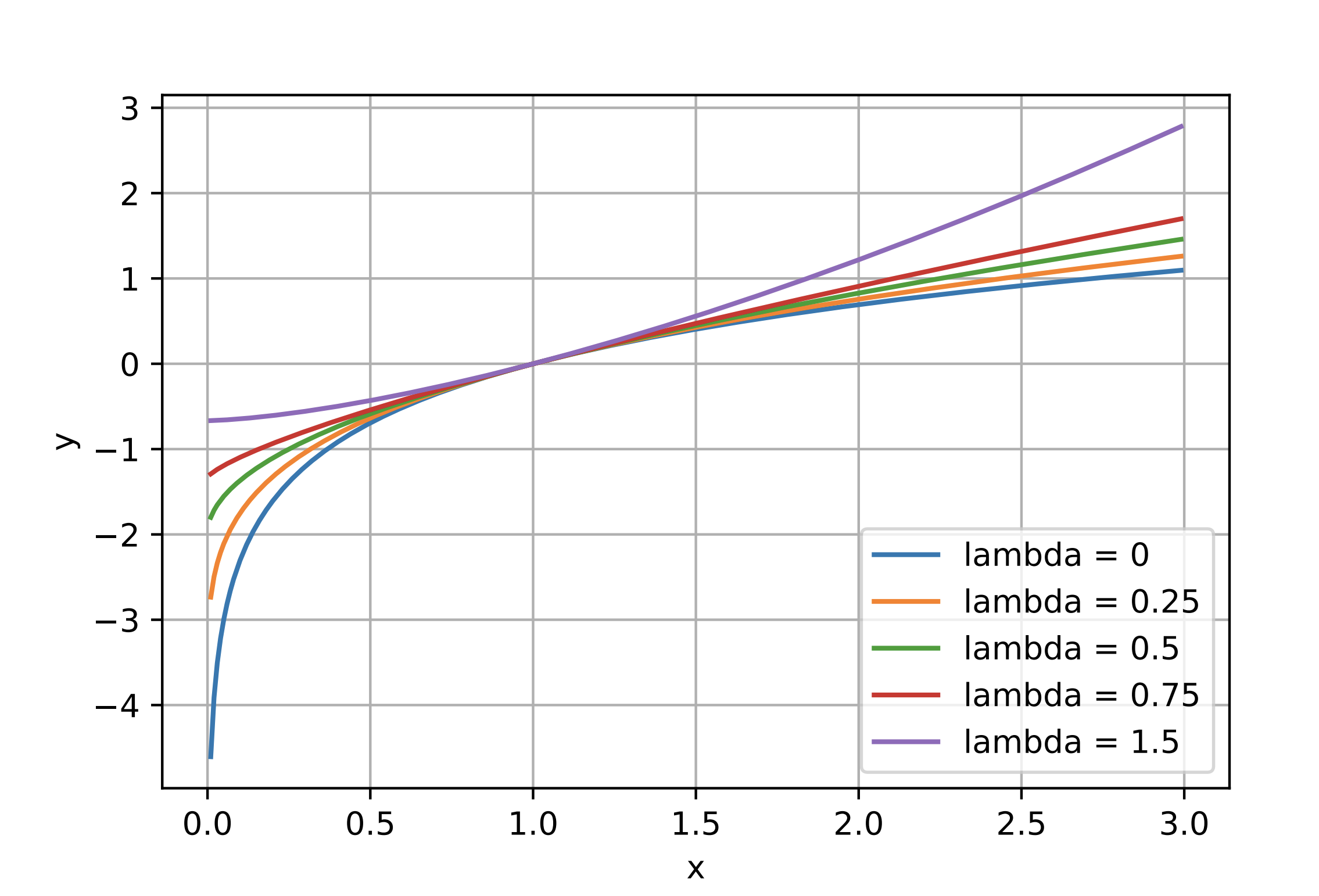
Box-Cox変換を使用するには事前にラムダの値を決める必要があります。ここで最尤法を用いることで変換後のデータが正規分布に最も近づくようにラムダを決定します。
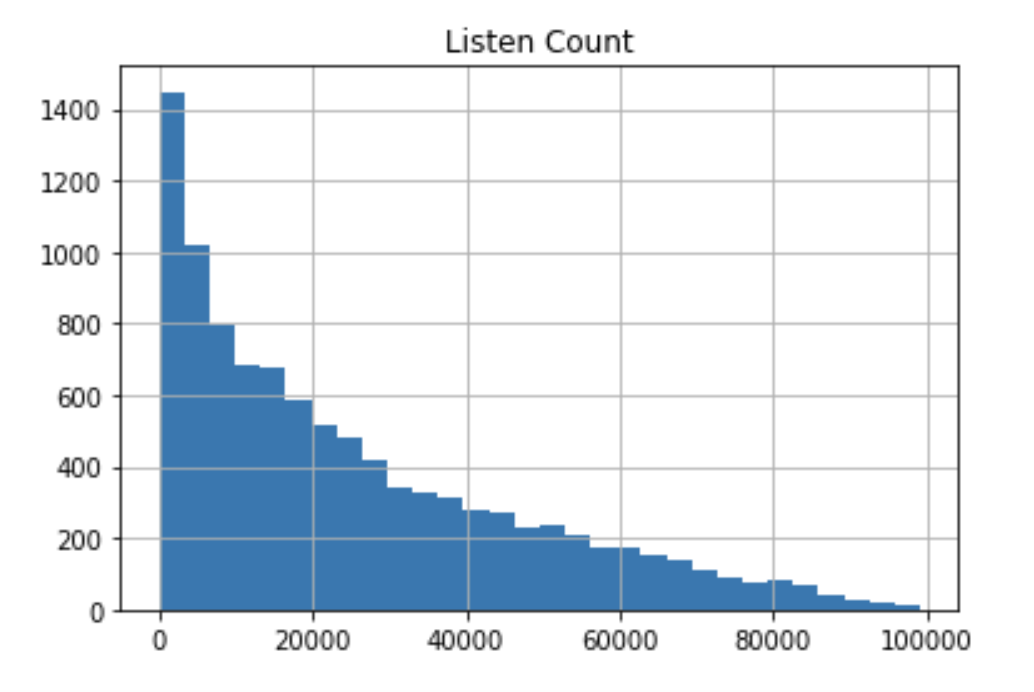
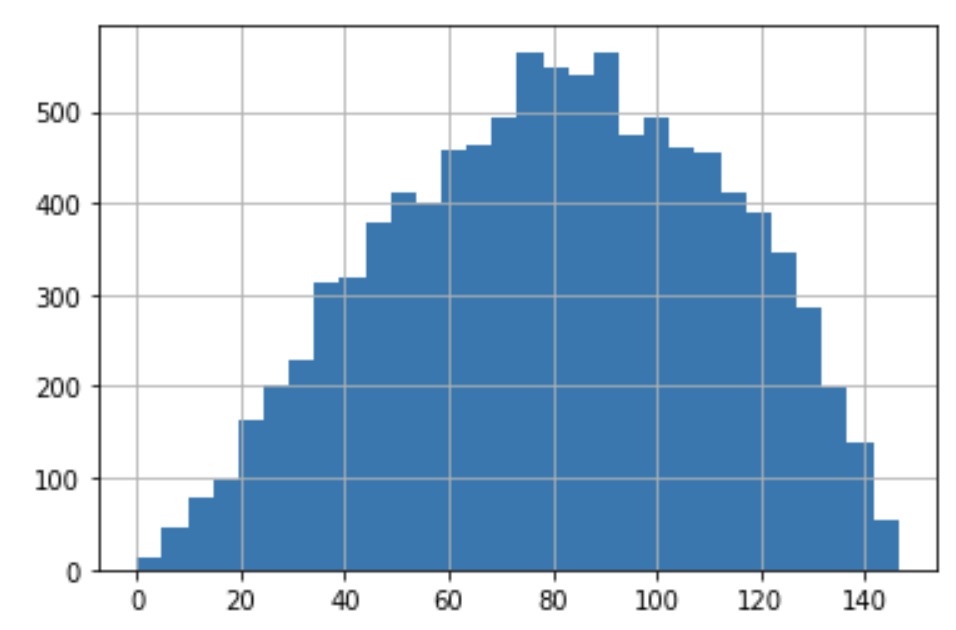
実際に下図のような分布をしたデータに対してBox-Cox変換を用いると、正規分布らしい分布に変換できていることがわかります。
Box-Cox変換適用前
Box-Cox変換適用後
Box-Cox変換適用のサンプルコード
from scipy import stats
import numpy as np
import pandas as pd
##乱数固定
np.random.seed(100)
##データ生成
data_array = []
for i in range(1, 1000):
s = np.random.randint(1, i * 100, 10)
data_array.extend(s)
data = pd.DataFrame({'Listen Count': data_array})
##Box-Cox変換
rc_bc, bc_params = stats.boxcox(data['Listen Count'])
print(bc_params) ##0.3419237117680786
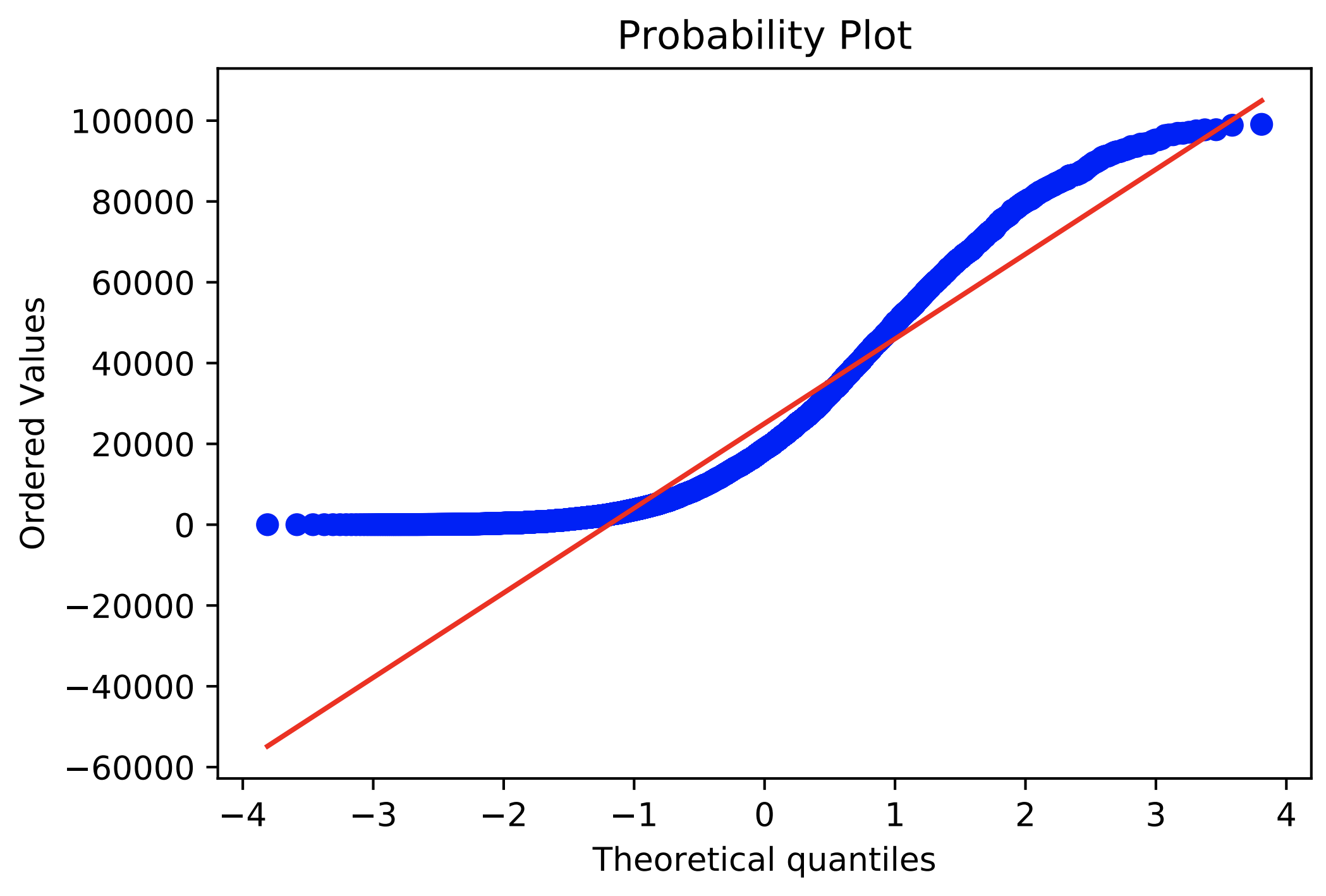
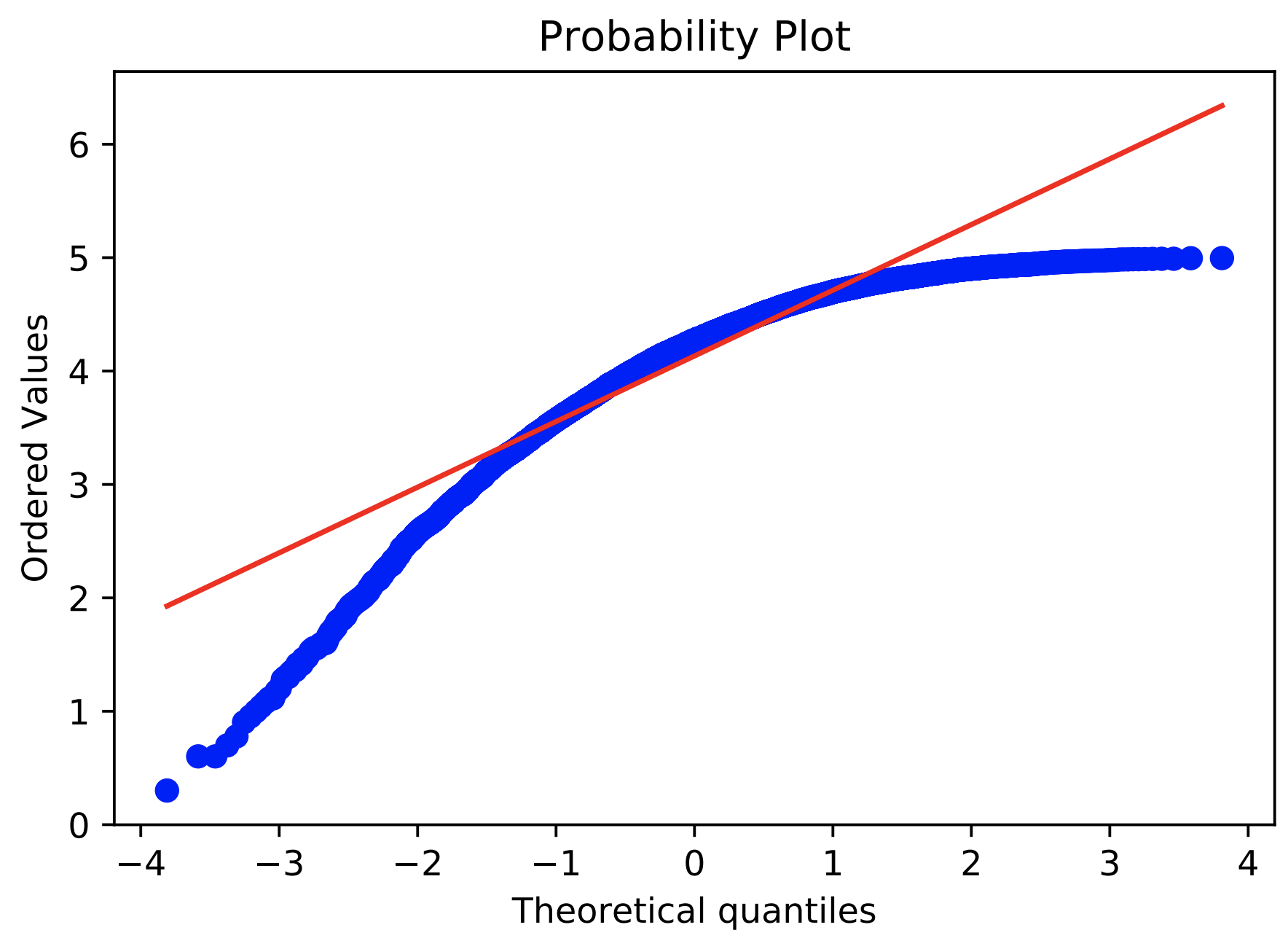
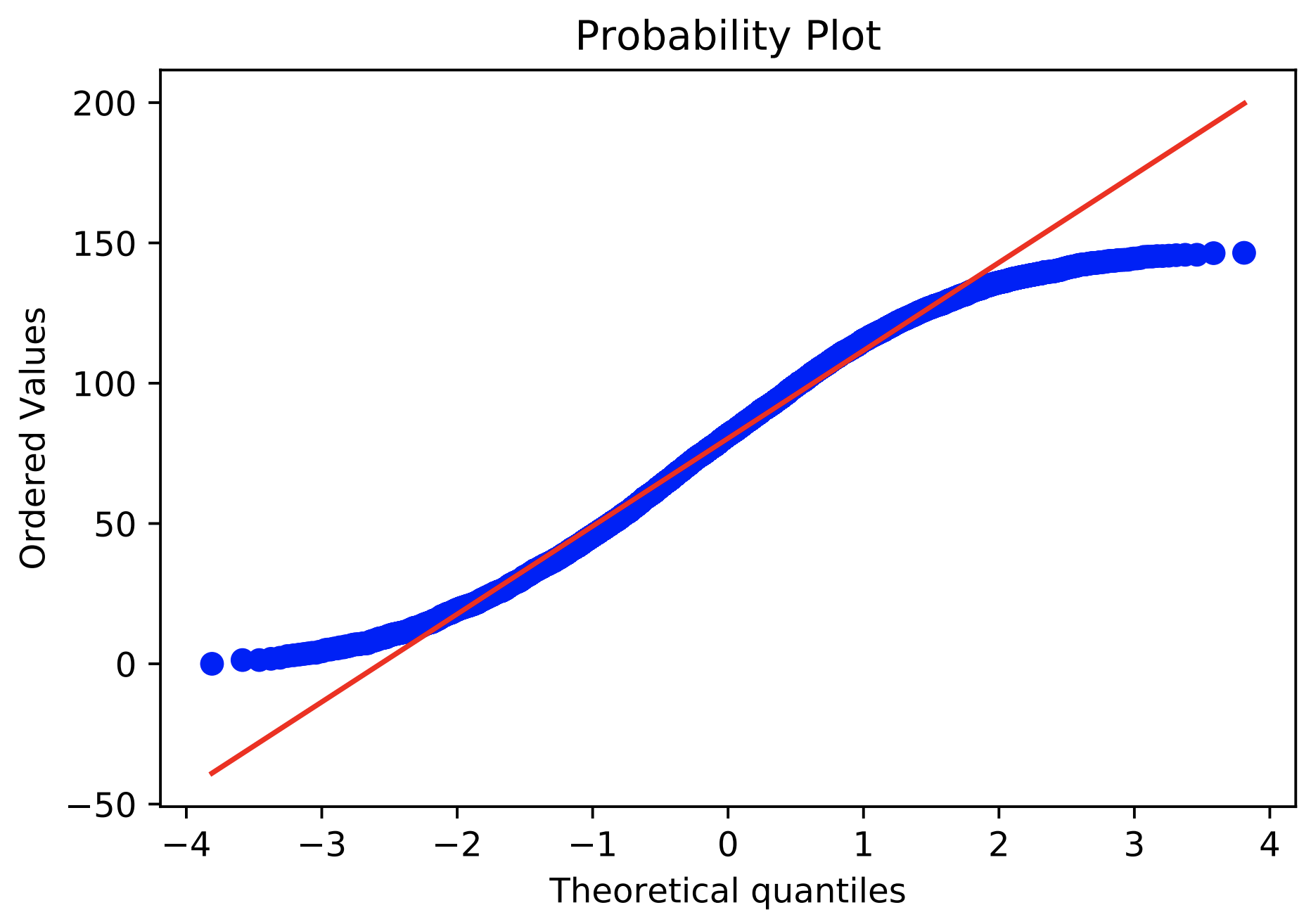
Q-Qプロット
Q-Qプロットは実測値と理想値をプロットしたものです。つまり、直線であれば、実測値は正規分布であると言うことができます。
以下に元データ、対数変換後のデータ、Box-Cox変換後のデータをプロットしたものを示します。
元データ
対数変換後
Box-Cox変換後
これらの結果からBox-Cox変換でもっとも正規分布に従わせることができたことが分かります。
最後に
YouTubeで機械学習を中心に技術書のレビューや解説動画を上げていこうと思っています。またIT系に行くなら知っておいた方がいい企業の紹介もやっています。YoutubeとQiita更新のモチベーションに繋がるため、いいね、チャンネル登録、高評価をよろしくお願い致します。
YouTube: https://www.youtube.com/channel/UCywlrxt0nEdJGYtDBPW-peg
Twitter: https://twitter.com/tatelabo
参考
https://yolo-kiyoshi.com/2018/12/26/post-1037/
https://toukei-lab.com/box-cox%E5%A4%89%E6%8F%9B%E3%82%92%E7%94%A8%E3%81%84%E3%81%A6%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83%E3%81%AB%E5%BE%93%E3%82%8F%E3%81%AA%E3%81%84%E3%83%87%E3%83%BC%E3%82%BF%E3%82%92%E8%A7%A3%E6%9E%90
https://toukeier.hatenablog.com/entry/2019/09/08/224346
https://sigma-eye.com/2018/09/23/qq-plot/