DBSCANのメリットを可視化して確認してみました。
DBSCANとは
最も一般的なクラスタリングアルゴリズムの一つで、データ点の密度を基に分類します。
パラメータはeps(ε)、minPtsの2つ。
各データ点は下記のロジックでコア点・(密度)到達可能点・外れ値に分類されます。
- 点 p がもし、p を含め、距離 ε(ε は p からの近傍の最大半径)以内に少なくとも minPts の点があれば、その点はコア点である。
- 点 q がもし、各 pi+1 が pi から直接到達可能(パス上のすべての点は、 q の可能な例外を持つ、コア点で無ければならない。)な、p1 = p かつ pn = q であるパス p1, ..., pn があれば、q は p から到達可能である。
- 他のどの点からも到達可能でないすべての点は外れ値である。
密度ベースのため
・球(超球)の形状を前提としない
・ノイズを分離できる
といったメリットがあり、例えばk-meansでは難しいこんなデータでも上手く分類可能(なはず)です。
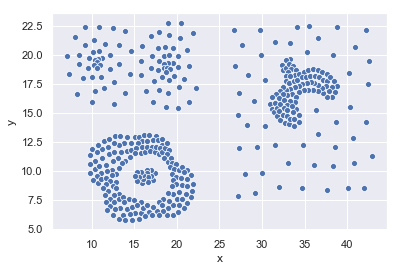
また、k-meansのようにクラスタ数を指定する必要はありません。
それではjupyter labで実際にクラスタリングしてみます。
例
ライブラリの読み込みとグラフの表示設定。scikit-learnを使います。
In[1]:
import pandas as pd
import numpy as np
import matplotlib as mpl
import seaborn as sns
from sklearn.cluster import DBSCAN
%matplotlib inline
sns.set()
datasetの読み込み。
In[2]
file = 'Dataset_Compound.csv'
df = pd.read_csv(file)
DBSCANの実施。
- eps(ε) = 0.1~5
- minPts = 5~30
の範囲で探索し、結果をDataFrameに入れてみます。
In[3]
columns=['eps','minPts','cluster_index','cluster_size']
df_dbscan = pd.DataFrame(columns=columns)
for eps in range(1,51):
eps /= 10
for minPts in range(5,31,5):
dbscan = DBSCAN(eps=eps,min_samples=minPts).fit(df)
labels = dbscan.labels_
clusters_index = np.unique(labels) #index of clusters, '-1' indicates noize points
clusters_size = np.bincount(labels+1) #size of each cluster
result = [eps, minPts, list(clusters_index), list(clusters_size)]
df_dbscan.loc[len(df_dbscan)] = result
クラスタ数6以上、ノイズ100未満の結果に絞って表示。
In[4]
filt = df_dbscan[columns[2]].map(lambda x: len(x)>5)
filt = filt & df_dbscan[columns[3]].map(lambda x: x[0]<100)
df_dbscan[filt]
Out[4]
| eps | minPts | cluster_index | cluster_size | |
|---|---|---|---|---|
| 54 | 1.0 | 5 | [-1, 0, 1, 2, 3, 4] | [97, 92, 15, 21, 158, 16] |
| 60 | 1.1 | 5 | [-1, 0, 1, 2, 3, 4] | [91, 92, 18, 24, 158, 16] |
| 66 | 1.2 | 5 | [-1, 0, 1, 2, 3, 4] | [85, 92, 22, 26, 158, 16] |
| 72 | 1.3 | 5 | [-1, 0, 1, 2, 3, 4] | [74, 92, 27, 32, 158, 16] |
| 73 | 1.3 | 10 | [-1, 0, 1, 2, 3, 4] | [90, 92, 20, 23, 158, 16] |
| 78 | 1.4 | 5 | [-1, 0, 1, 2, 3, 4] | [64, 92, 28, 41, 158, 16] |
| 79 | 1.4 | 10 | [-1, 0, 1, 2, 3, 4] | [87, 92, 21, 25, 158, 16] |
| 84 | 1.5 | 5 | [-1, 0, 1, 2, 3, 4] | [59, 93, 31, 42, 158, 16] |
| 85 | 1.5 | 10 | [-1, 0, 1, 2, 3, 4] | [83, 93, 22, 27, 158, 16] |
| 86 | 1.5 | 15 | [-1, 0, 1, 2, 3, 4] | [99, 92, 15, 21, 156, 16] |
上手く分類できていそう。
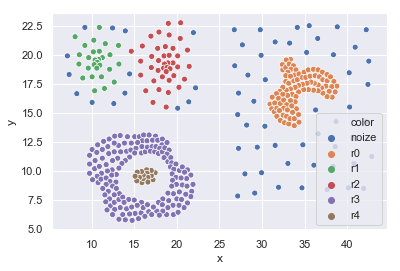
78番目をグラフで確認してみます。
In[5]
index = 78
eps = df_dbscan[columns[0]][index]
minPts = df_dbscan[columns[1]][index]
dbscan = DBSCAN(eps=eps,min_samples=minPts).fit(df)
labels = dbscan.labels_
X = df.copy()
X['labels'] = labels
X['color'] = X.labels.map(lambda x: 'noize' if x<0 else 'r'+str(x)) #色分けのためにcategorical dataを作成
X.sort_values('color')
sns.scatterplot(x='x', y='y', data=X, hue='color')
右側:ノイズを上手く切り分けられています。
左下:ドーナツ型(紫)とその内部(茶)を上手く切り分けられています。
左上:他のクラスタと密度に違いがあり、周囲がノイズと判定されています。
まとめ
DBSCANの下記のメリットが確認できました。
- 球(超球)の形状を前提としない
- ノイズを分離できる
- クラスタ数の指定が必要ない
反対に、デメリットには下記が挙げられるようです。
- クラスタの密度に差が大きいと上手くクラスタ分けできない
eps, minPtsのパラメータで全クラスタの密度を決めるからですね。
階層クラスタリングによる解決がありえます。 - 計算コストが高い
全データ点を対象とした計算を反復して行うため。
今回程度の計算量では気になりませんが、次元の増加に弱い、リアルタイムのアプリケーションには実装しにくいなど言われています。
Dataset References:
Compound: C.T. Zahn, Graph-theoretical methods for detecting and describing gestalt clusters. IEEE Transactions on Computers, 1971. 100(1): p. 68-86.