Python初学者のためのメモ

はじめに

　この記事は、大学1,2年生で大学の授業で少しプログラミングの授業を受けた学生に対して、pythonを実際に動かしながら実験データの解析をする方法を紹介している。

Colaboratoryを使ってpythonコードを実行する。

　ColaboratoryはGoogleが提供している環境で、ブラウザ上でpythonを記述し、クラウドサーバー上でコードの実行を可能とする。自分の使っているパソコンの性能に依らず、GPUやTPUなどのGoogleのハードウェアを活用できることが一番のメリットである。

使い方

　ブラウザ上でColaboratoryと検索し以下のページに行く。左上の”ファイル”を選択し、ノートブックを新規作成を選択する。

Googleドライブをマウントする。

　Googleドライブ内のデータにアクセスするためにGoogleドライブに接続(マウントと言う)する。colaboratoryのセルに下記をコピーし、左側の三角マークを押して実行する。

from google.colab import drive
drive.mount('/content/drive')

『このノートブックにGoogleドライブのファイルへのアクセスを許可しますか？』と確認されるので、右下のGoogleドライブに接続を選ぶ。さらに、アカウント選択画面が別に出てくるので、自分のアカウントを選択し、「次へ」を選択し、「続行」を選択する。

自分のGoogleドライブが見えているかを確認

　次に実行したセルの下の方にカーソルを持っていくと+コードが出てくるので、+コードを選択し新たにセルを追加する。

!ls /content/drive/MyDrive/

自分のGoogleのMyDriveの中身が見えてれば成功。

作業スペースを作成(2回目以降は必要ない)

作成した図の保存やデータを保存するための作業スペース(フォルダ)を作成する。

!mkdir /content/drive/MyDrive/BasicExperiment

出来ているか確認する。

!ls /content/drive/MyDrive/

「BasicExperiment」が表示されていれば成功。

Pythonを使った実験データの解析

解析のための準備

以下のURLからデータをダウンロードして、GoogleドライブのBasicExperimentに入れておく。

解析に使うCSVデータ(noise.csv)を以下のURLに置いてある。
https://drive.google.com/file/d/1sgoKwJ8S57PnjXnkKOnfudfu_Zs1JpwJ/view?usp=sharing

データの読み込み

pythonには、様々な便利なモジュールと呼ばれるツールがある。
データを読み込むのはpandasと呼ばれる便利なモジュールを用いる。
新しく、セルを追加して以下を実行する。

import pandas as pd

filename = "/content/drive/MyDrive/BasicExperiment/noise.csv"

df = pd.read_csv(filename,skipfooter=11,usecols=[0,1],names=['time','voltage'])

説明

1行目

pandasというモジュールをインポートする。モジュールを呼び出して使う際に毎回pandasと書くの面倒なので、as pdとしてpdにpandasを入れて使えるようにしておく。

2行目

ファイルの場所と名前を指定する。この"/"で始まる場所をPATH(パス)という。

3行目

pandasの中にread_csvという関数がある。最初の引数はファイルの場所と名前を指定する。今回の実験データは最後の11行にフッターがついているのでskipfooterで最後の11行を読み出さずにスキップする。usecolsは使う列を指定している。今回は1行目と2行目を読み出したいので、0と1を指定する(Pythonでは1行目が0)。names=['time','voltage']はcsvファイルにヘッダーがないので、列に名前を付ける。
これでdfという変数に読み込んだデータを入れることができた。
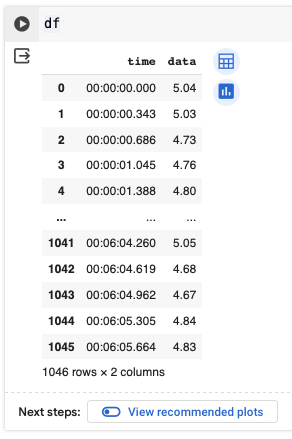
データが正常に読み込まれたかを確認する。dfと打って実行。

df

以下のように表示されれば成功。

このまま"df"を扱っても良いが、このデータには時間と電圧データの2系列のデータが入っていて、初心者に時間の取り扱いは煩雑なので、以下の方法でnumpy.arrayとしてdata変数に電圧データ部分だけ格納する。

data = df['voltage'].values
print(data) #データの中身を確認。

df['voltage']で"voltage"の列をしている。.valuesでデータの値だけを持ってくることができる。

Pythonを用いたデータの取り扱い

実験データの基本的な量である平均値、標準偏差、不偏標準偏差などを確認方法

実験データのような複数の行や列があるものを取り扱うには、numpyというモジュールを用いる。

import numpy as np

data_num  = len(data)            #データの個数
data_min  = min(data)            #データの最小値
data_max  = max(data)            #データの最大値
data_ave  = np.average(data)     #平均値の計算
data_sig  = np.std(data)         #標準偏差の計算
data_usig = np.std(data, ddof=1) #不偏標準偏差の計算は引数のddof=1を指定する。

#それぞれの値を表示する。
print(f"Number of data = {data_num}")               #データの個数
print(f"Maximum value = {data_max}")                #データの最大値
print(f"Minimum value = {data_min}")                #データの最小値
print(f"Average value of data = {data_ave}")        #平均値
print(f"Standard Deviation = {data_sig}")           #標準偏差
print(f"Unbiased Standard Deviation = {data_usig}") #不偏標準偏差

標準偏差と不偏標準偏差は似ているが、明確に違いがあるの注意すること。一般に物理で測定された測定データの平均値は推定値なので不偏標準偏差を用いる。

print()関数で表示される数値を、そのままレポートや論文に書くと有効数字を間違うことになるので注意すること。

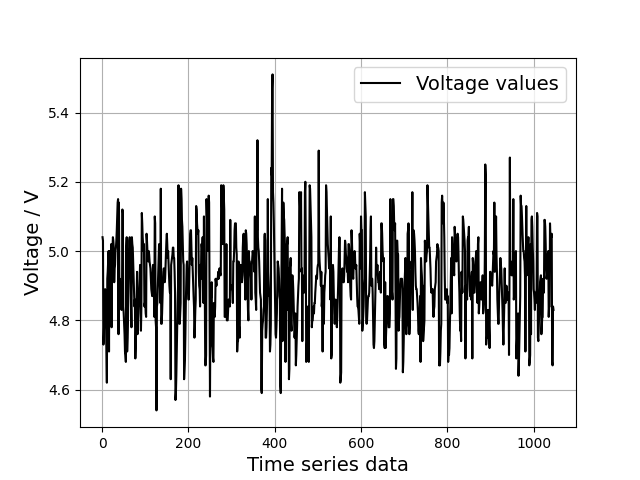
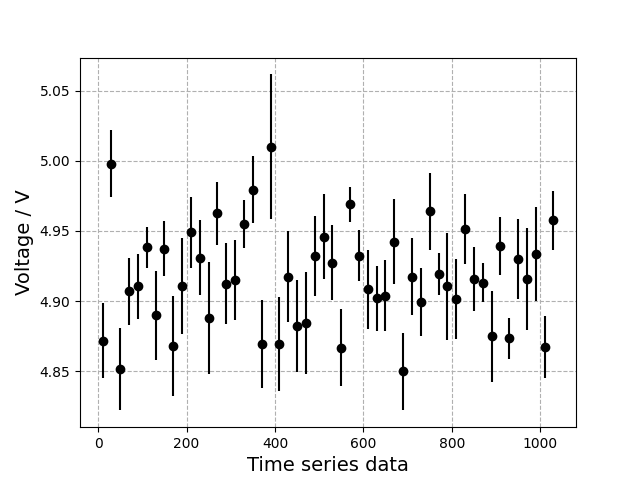
実験データの時間変動の確認(図のプロット1)

コード

import matplotlib.pyplot as plt

x_data = np.arange(1, data_num+1, 1) 

plt.plot(x_data, data, color='k')                #データのplot
plt.xlabel('Time series data', fontsize=14) #X軸のラベル
plt.ylabel('Voltage / V', fontsize=14)      #Y軸のラベル
plt.legend(['Voltage values'], fontsize=14) #凡例を入れられる。
plt.grid()                                  #グリッドを入れる

#データの保存
plt.savefig('/content/drive/MyDrive/BasicExperiment/fig1.png')

#pdfで保存したい場合は最後の拡張子をpdfに変更する。
#plt.savefig('/content/drive/MyDrive/BasicExperiment/fig1.pdf')

結果(figA1.png)

説明

1行目
データのプロットには、matplotlibのモジュール内あるmatplotlib.pyplotを用いる。

2行目
図をプロットするには、縦軸の値(今回は電圧のデータ)と横軸の値(今回は時系列)を用意する必要がある。numpyの中のnp.arange関数を用いて、1から1046までを1間隔で用意する。

3行目
plotする関数、1番目の引数にx軸の値を入れて、2番目の引数にy軸のデータを入れる。3つ目以降の引数で、プロットするマーカー種類やサイズ、色などを指定できる。今回はcolor='k'として色を黒に指定している。

4行目、5行目
x軸のラベルとy軸のラベルを付ける。fontsize=14で文字サイズを14 ptに指定している。通常、プログラムのコード中に日本語を使うのは推奨しない(コメントアウトを除く)。

6行目
凡例を入れられる。

7行目
図にグリッド線を入れる。

8行目
図の保存を行う。一般的には、図の拡張子はpdfを使うことが多いが、図のファイルサイズが大きすぎる場合はpngを使うこともある。今回は、pngファイルで保存しておく。

図を保存する際に同じ名前にしてしまうと勝手に上書き保存されてしまうので、名前を変え忘れないように注意すること。

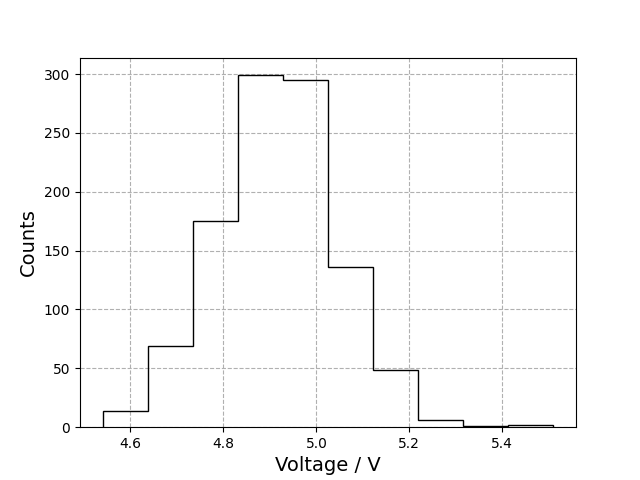
実験データの頻度分布(ヒストグラム)の確認(図のプロット2)

ヒストグラムのデータは横軸に階級数(bin数と呼ぶ)、縦軸に頻度がくる。今回はmatplotlib.pyplot内にあるhist関数を用いてplotする。

import matplotlib.pyplot as plt

n, bins, _ = plt.hist(data, bins=10)
plt.xlabel('Voltage/V', fontsize=14)
plt.ylabel('Counts', fontsize=14)

plt.savefig('/content/drive/MyDrive/BasicExperiment/fig2.png')

結果(fig2.png)

説明

2行目
plt.histを使ってヒストグラムを描画できる。一つの目の引数には電圧データを入れる。2つ目の引数であるbins=10は幾つの階級に分けるかを入れる(今回は10binに分けた)。binsの値を変えてみると形が変わるので、試してみるといい。

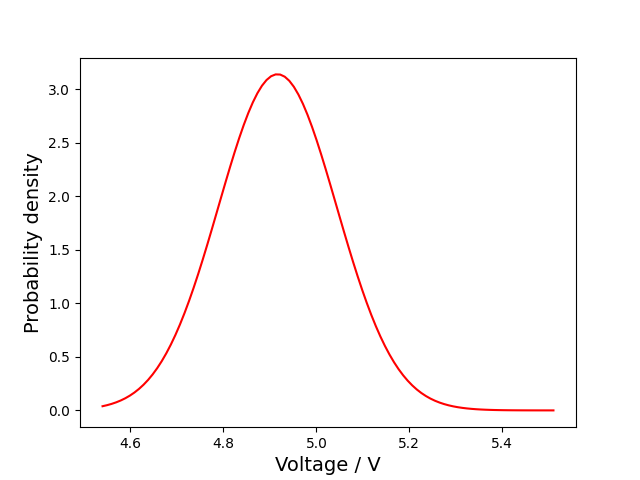
ガウス分布関数のプロット(プロット3)

ガウス関数のような複雑な関数はコードで書く際に間違えやすいので、scipyと呼ばれる科学計算に特化したモジュールを使った方が良い。

コード

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm #scipyからガウス関数を読み込む

x_g = np.linspace(data_min, data_max, 100) #dataの最小値から最大値までを100点用意
y_g = norm.pdf(x_g, data_ave, data_usig)   #norm.pdf(x軸データ, 平均値, 不偏標準偏差)
plt.plot(x_g, y_g, color='r')              #colorで色を指定可能
plt.xlabel('Voltage/V', fontsize=14)
plt.ylabel('Probability density', fontsize=14) 

plt.savefig('/content/drive/MyDrive/BasicExperiment/fig3.png') 

結果(fig3.png)

説明

3行目
scipy.statsの中にあるnormモジュールにガウス分布に関する関数が入っている。

4行目
ガウス分布の描画範囲の指定。今回は、データのヒストグラムと比較したいので、ヒストグラムの最大値から最小値までのデータを100分割したx軸を用意している。

5行目
ガウス関数の計算。引数の最初にx軸の値、2つ目に、平均値、3つ目に不偏標準偏差を入れると、ガウス分布が計算される。

---

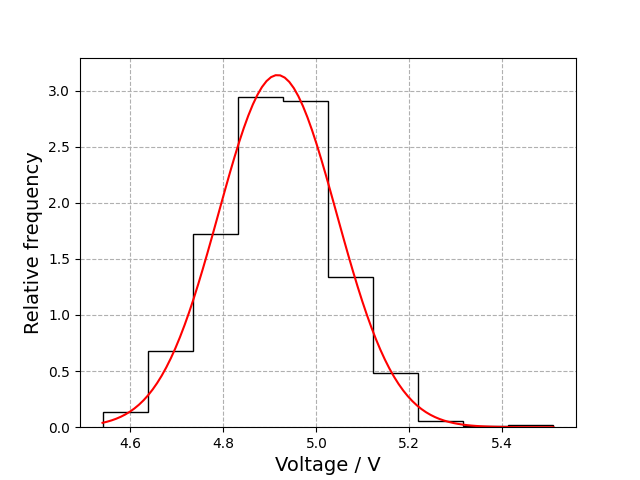
実際のデータとガウス分布の比較

コード

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm #scipyからガウス関数を読み込む

#実際のデータの描画
n, bins, _ = plt.hist(data, bins=10, histtype='step', density=True, label='measured value', color='k')

#ガウス関数の描画
x_g = np.linspace(data_min, data_max, 100) #dataの最小値から最大値までを100点用意
y_g = norm.pdf(x_g, data_ave, data_usig)   #norm.pdf(x軸データ, 平均値, 不偏標準偏差)
plt.plot(x_g, y_g, color='r')              #colorで色を指定可能
plt.grid(ls='--')
plt.xlabel('Voltage/V', fontsize=14)
plt.ylabel('Relative frequency', fontsize=14)

plt.savefig('/content/drive/MyDrive/BasicExperiment/fig4.png') 

結果(fig4.png)

説明

実際のデータのヒストグラムを表示するときはガウス関数とスケールを合わせる必要があるため、plt.hist関数の引数のdensity=Trueとする。

扱うデータの個数と平均値の関係

コード

データを5個ごとにまとめて、その平均値を計算する。

import numpy as np

y5a1 = np.average(data[0:5])  #1番目から5番目のデータを取り出し、そのデータの平均値を計算
y5a2 = np.average(data[5:10]) #5番目から10番目のデータを取り出し、その平均値を計算
y5a3 = np.average(data[10:15])
y5a4 = np.average(data[15:20])
y5a5 = np.average(data[20:25])

y5a = np.array([y5a1, y5a2, y5a3, y5a4, y5a5]) #5個ごとの平均値を一つのアレイにして用意
print(y5a)

説明

data[0:5]とすることで、data配列の1番目から5番目までのデータを取り出すことができる。それをnumpyのaverage関数に入れて平均値を計算している。

np.array([])は、配列を作る関数である。こうすることで、5個ごとの平均値を一つのアレイにして用意した。

この書き方では、1000個のデータを5個ごとに平均していくと200行必要になるので大変なことが分かる。そこで、同じ処理をもっと簡単にかつ、色々な分割数に対応した関数を自分で用意してみる。

分割する関数のコード

import numpy as np

def splitting_data(data, N):
    data = data
    N = int(N)

    data_num = len(data)                    #データの個数の確認
    
    remainder = data_num % N                    #余りを計算
    cut_num   = int(data_num-remainder)
    data_cut  = data[:cut_num]              #データ個数の調整
    sp_num    = int(cut_num/N)             #分割数
    data_sp   = data_cut.reshape(sp_num, N) #N個ごとに分割

    sp_ave_list = np.average(data_sp, axis=-1)             #分割数ごとの平均値を計算
    sp_sig_list = np.std(data_sp, ddof=1, axis=-1)/np.sqrt(N) #分割数ごとの標本平均の標準偏差を計算

    sp_sig = np.std(sp_ave_list, ddof=1)

    #plot用のx軸も用意しておく。
    sp_x = np.arange(0, cut_num, N)+(N/2.)
    
    return sp_x, sp_ave_list, sp_sig_list, sp_sig

説明

reshape関数を使ってlistを分割している。

この関数では4つの値を返り値として設定している。
sp_xは分割した際の新しいx軸の値
sp_ave_listは、分割したデータ毎の平均値のリスト
sp_sig_listは、分割したデータ毎の標本の標準偏差
sp_sigは、分割して計算した平均値の標準偏差

時系列データを20個毎に分割して描画するコード

import matplotlib.pyplot as plt

n = 20 #２０個毎に分割

sp_x, sp_ave_list, sp_sig_list, sp_sig = splitting_data(data, n) #作った関数を呼び出す

#N個ごとに分割した時間変動を誤差込みで描画
plt.errorbar(sp_x, sp_ave_list, yerr=sp_sig_list, fmt='ko') #誤差棒をplotするときはplt.errobar関数を使う
plt.xlabel('Time series data', fontsize=14) #X軸のラベル
plt.ylabel('Voltage / V', fontsize=14)        #Y軸のラベル
plt.grid(ls='--')

20個ごとに分割した時系列データの結果

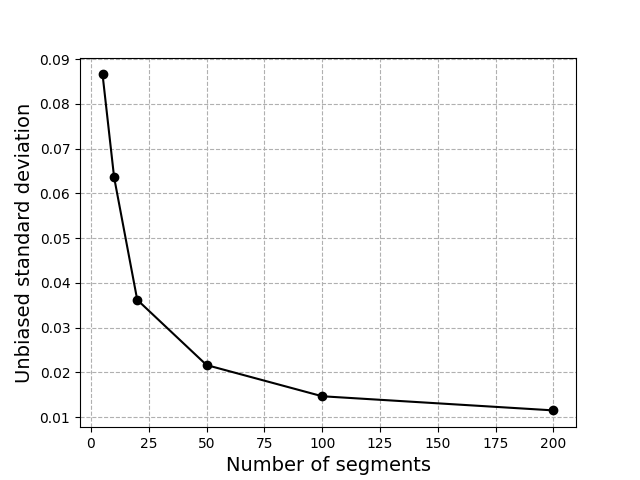
分割したデータ数とその不偏標準偏差の関係

N=5,10,20,50,100,200で、それぞれ分割した際の平均値の不偏標準偏差がどうなるかを確認する。

sig_list = []
n_list = [5, 10, 20, 50, 100, 200]

for n in n_list:
    sp_x, sp_ave_list, sp_sig_list, sp_sig = splitting_data(data, n) #作った関数を呼び出す
    sig_list.append(sp_sig)

plt.plot(n_list, sig_list, "ko-")
plt.xlabel('Number of segments', fontsize=14)
plt.ylabel('Unbiased standard deviation', fontsize=14)
plt.grid(ls='--')
plt.savefig('/content/drive/MyDrive/BasicExperiment/fig5.png') 

結果(fig5.png)

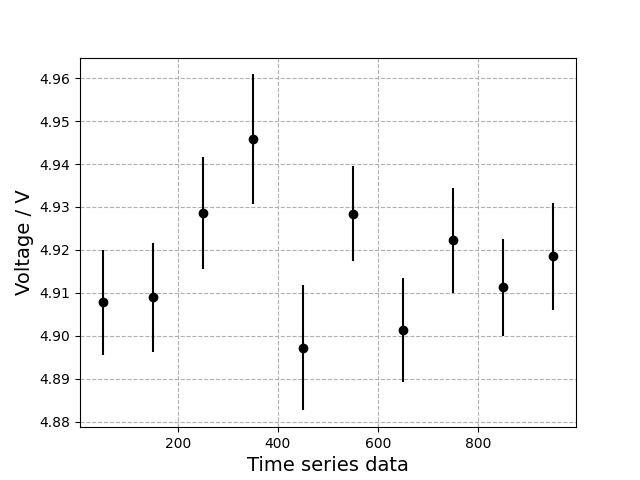
N=100で分割した際の時間変動の確認

誤差棒を図に表示する際は、plt.errorbar()関数を使う。yerrに誤差を入れると誤差棒を表示していくれる。

import matplotlib.pyplot as plt

N = 100
sp_x, sp_ave_list, sp_sig_list, sp_sig = splitting_data(data, N) #作った関数を呼び出す

#N個ごとに分割した時間変動を誤差込みで描画
plt.errorbar(sp_x, sp_ave_list, yerr=sp_sig_list, fmt='ko') #誤差棒をplotするときはplt.errobar関数を使う
plt.xlabel('Time series data', fontsize=14) #X軸のラベル
plt.ylabel('Voltage / V', fontsize=14)        #Y軸のラベル
plt.grid(ls='--')

plt.savefig('/content/drive/MyDrive/BasicExperiment/fig6.png')

結果(fig6.png)

最小二乗法(直線回帰)

　物理実験では、求めたい物理量を直接観測できず、得られた一連のデータから解析して求める場合がある。測定された実験データとその誤差を加味し、最適化なモデルのパラメータを求めるためには、最小二乗法が用いられる。

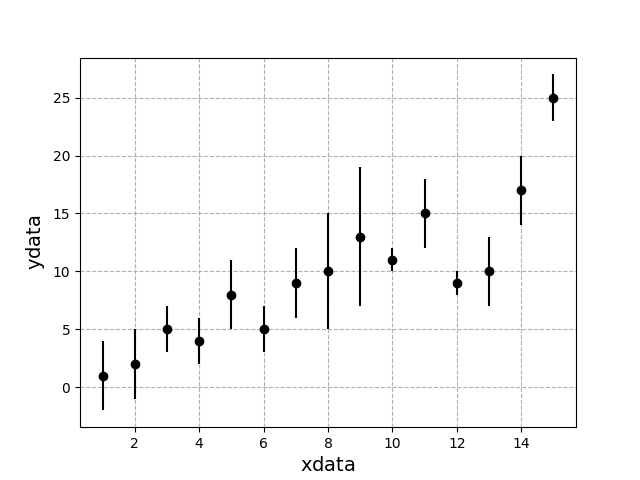
ここでは、以下の実験データをもとに最小二乗法について解説する。

xdata = np.array([1, 2, 3, 4, 5, 6, 7,  8,  9, 10, 11, 12, 13, 14, 15])
ydata = np.array([1, 2, 5, 4, 8, 5, 9, 10, 13, 11, 15,  9, 10, 17, 25])
sigma = np.array([3, 3, 2, 2, 3, 2, 3,  5,  6,  1,  3,  1,  3,  3,  2])

このデータを$y=ax+b$の直線で再現できるとし、上のデータを上手く説明できる$a,\ b$を最小二乗法を用いて求める。
また、最小二乗法は、

\Delta = \sum_i \frac{x_i^2}{\sigma_i^2} \sum_i\frac{1}{\sigma_i^2} - \left( \sum_i \frac{x_i}{\sigma_i^2} \right)^2 \label{1}

とすると

a = \left( \sum_i \frac{x_i y_i}{\sigma_i^2}\sum_i \frac{1}{\sigma_i^2} - \sum_i \frac{x_i}{\sigma_i^2}\sum_i\frac{y_i}{\sigma_i^2} \right)/\Delta

b = \left( \sum_i \frac{x_i^2}{\sigma_i^2}\sum_i \frac{y_i}{\sigma_i^2} - \sum_i \frac{x_i y_i}{\sigma_i^2} \sum_i \frac{x_i}{\sigma_i^2}\right)/ \Delta

と書くことができる。また、aとbの誤差は、

\sigma_a=\sqrt{\sum_i\frac{1}{\sigma_i^2}/\Delta},

\sigma_{b}=\sqrt{\sum_i\frac{x_i^2}{\sigma_i^2}/\Delta},

と書くことができる。

これをpythonを用いて書くと以下のように書ける。

最小二乗法の関数の定義

import numpy as np

def cal_leastsq(xdata, ydata, sigma):
    """
    与えられたデータに対して最小二乗法を用いて直線のフィットを行い、その結果と誤差を計算する関数
    
    Parameters:
        xdata : numpy.ndarray
            x軸のデータ
        ydata : numpy.ndarray
            y軸のデータ
        sigma : numpy.ndarray
            yの誤差のデータ
        
    Returns:
        a : float
            フィットされた直線の傾き
        b : float
            フィットされた直線の切片
        a_err : float
            フィットされた直線の傾きの誤差
        b_err : float
            フィットされた直線の切片の誤差
        chisq_min : float
            最小のカイ二乗値
    """
    x = xdata
    y = ydata
    s = sigma

    delta = ( (sum((x**2)/(s**2))) * (sum(1./(s**2))) ) - ( (sum(x/(s**2)))**2 )
    a     = ( ( (sum((x*y)/(s**2))) * (sum(1/(s**2))) ) - ( (sum(x/(s**2))) * (sum(y/(s**2))) ) )/delta
    a_err = np.sqrt(sum(1/(s**2))/delta)
    b     = ( sum(x**2/(s**2))*sum(y/(s**2)) - (sum(x*y/(s**2)))*(sum(x/(s**2))) )/delta
    b_err = np.sqrt((sum(x**2/s**2))/delta)
    
    # χ^2_min (最小のカイ二乗値) を計算
    fit_values = a * x + b               #フィットから予測された値
    residuals = (y - fit_values) / sigma #ydataと直線の残差/sigma
    chisq_min = np.sum(residuals**2)     #χ2min

    return a, b, a_err, b_err, chisq_min

この関数を使って、データを再現する最適な直線の傾きと切片を求める。

import numpy as np
import matplotlib.pyplot as plt

#サンプルデータ
xdata = np.array([1, 2, 3, 4, 5, 6, 7,  8,  9, 10, 11, 12, 13, 14, 15])
ydata = np.array([1, 2, 5, 4, 8, 5, 9, 10, 13, 11, 15,  9, 10, 17, 25])
sigma = np.array([3, 3, 2, 2, 3, 2, 3,  5,  6,  1,  3,  1,  3,  3,  2])

#定義した関数を使って計算
a, b, a_err, b_err, chisq_min = cal_leastsq(xdata=xdata, ydata=ydata, sigma=sigma) #作った関数を呼び出す。
print(f'a={a} +- {a_err}')
print(f'b={b} +- {b_err}')
print(f'chi2_min = {chisq_min}')
#換算χ2を計算、パラメータの数が2なので自由度はN - 2
print(f'reduced chi-squared = {chisq_min/(len(ydata)-2)}')

#plot
y_fit_data = a * xdata + b
plt.errorbar(xdata, ydata, yerr=sigma, fmt='ko', label='data')
plt.plot(xdata, y_fit_data, 'r-', label='fit results')
plt.xlabel(r'$\rm xdata$', fontsize=14)
plt.ylabel(r'$\rm ydata$', fontsize=14)
plt.legend(fontsize=14)
plt.grid(ls='--')

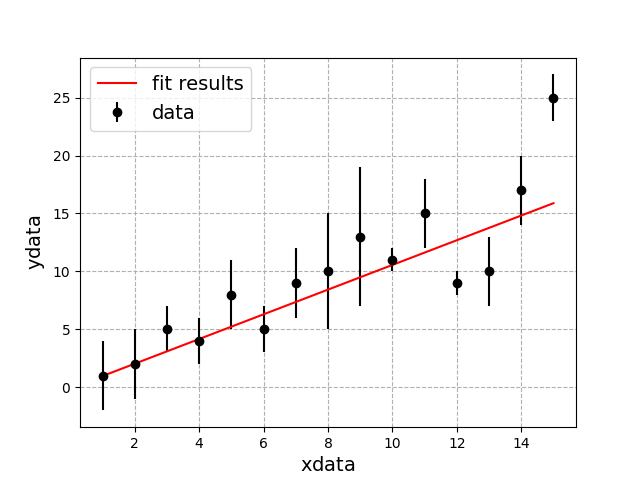
このように、データにあう最適な$y=ax+b$の直線を引くことができる。

　このcal_leastsq()関数では、1次関数($y=ax+b$)形のみでFittingできるが、特殊な事例においては活用することができる。その例を紹介する。
$N_{0}$個の放射線が、ある厚み$x$で線吸収係数$\mu$の物質に入射した際の透過個数は、

N(x)=N_{0} e^{-\mu x}

のように書ける。この式は非線形な形であり、このままではcal_leastsq()関数を使うことは出来ない。そこで、対数を取ることで、

logN(x)=-\mu x + logN_{0}

と変形でき、$logN(x)$をy、$-\mu$をa、$logN_{0}$をbと置くと、

y=ax+b

と書くことができ、cal_leastsq()関数を使うことができる。このように1次関数の形に変更することができれば、cal_leastsq()関数を応用することができる。

おわりに

　今回は、pythonを用いて物理実験のデータ解析方法の基本的な方法を紹介した。