はじめに
物理法則のシミュレーションや最適化問題などにおいて,大規模な連立一次方程式を解くというタスクの重要性はますます高まっている.具体的には
$$\mathbf{A}\mathbf{x}=\mathbf{b}$$
という格好の方程式を効率よく解くことが求められている.ここで,$\mathbf{A}$ は何らかの行列,$\mathbf{x}, \mathbf{b}$ は何らかのベクトルであり,
$\mathbf{A}$ および $\mathbf{b}$ が与えられた時に,方程式 $\mathbf{A}\mathbf{x}=\mathbf{b}$ を満たす $\mathbf{x}$ を求めよ
といった形で定式化される問題は枚挙にいとまがない.例えば,シミュレーションといえば
- 有限要素法・差分法・境界要素法などを用いて離散化された偏微分方程式
といったものを思い浮かべる人が一定数いると思う.さらに,ちょっとだけ一般化して
$$I[\mathbf{x}] := \|\mathbf{A}\mathbf{x} - \mathbf{b}\|^{2}$$
という二次形式を定義してやれば,$(\mathbf{A}, \mathbf{b})$ を適当に設計すれば様々な計画問題を表現できるということも理解してもらえると思う.
というわけで,方程式 $\mathbf{A}\mathbf{x}=\mathbf{b}$ を解くというタスクの需要は大きいのである.
一方で,これを解く方法は次の3種類に分類できる.
- 行列 $\mathbf{A}$ の逆行列を余因子展開によって求め,それを方程式の両辺の左から掛ける(線形代数的手法)
- 行列 $\mathbf{A}$ を $\mathbf{A} = \mathbf{L} \mathbf{U}$ という筋の良い形に分解し(多くの場合 $\mathbf{L}$ と $\mathbf{U}$ がそれぞれ下三角行列,上三角行列なのでLU分解と呼ばれる),逐次的に $\mathbf{L}$ と $\mathbf{U}$ を消去する(直接法).
- 方程式の真の解 $\mathbf{x}$ に収束するようなベクトル列 ${\mathbf{x}_{k}}$ を構成する(反復法)
これらのうち,最も計算回数のコストが掛かるのが1つ目の線形代数的手法である.これを実際の数値計算に採用したならば,とても使い物にならないアルゴリズムになる.それでは,残り2つはどうなのかというと,
- 直接法は並列化が困難だが,$\mathbf{A}$ が密行列の場合にはほぼ唯一の安定手法で,計算回数・メモリ使用量は並列化の有無で異なる
- 反復法は$\mathbf{A}$ が疎行列の場合にはパフォーマンスが上がりやすく,並列化が容易
といった違いがある.一方,産業におけるニーズでいえば,たぶん $\mathbf{A}$ が疎行列になっているケースの方が多いんじゃなかろうか(ここらへんはちょっと自信ないです).というわけで,我々は反復法を極めないといけないのである.
最初の話に戻ると,現代社会におけるこういった問題を解くニーズは,$\mathbf{A}$ のサイズを大きくする方向に成長しているとも言える.同じ大きさの空間で問題を解く場合には,高精度化(メッシュの細分化)が $\mathbf{A}$ の肥大化につながるし,精度を維持してもより大きな空間で解くとなると同じく $\mathbf{A}$ を大きくせねばならない.問題なのは,こうした肥大化が指数関数的な成長であるという点である.一方,並列化が容易な反復法を採用し続ける限り,大規模な多ノード計算機環境やGPUによる並列計算でカバーすることもできる.
以上の背景もあり,本記事では反復法の最も簡単なケースであるJacobi法の実装とその計算結果を紹介する.
なお,Jacobi法は反復法を
- 定常反復法
- 非定常反復法
という2つのクラスに大別した時の定常反復法に属するアルゴリズムである.現代だと,実際の応用で定常反復法だけを使って問題が解かれるケースはむしろ減っているが,定常反復法はその数学的に簡便で理解しやすい,収束解析がしやすい,などのメリットから理論的には極めて重要である.
Jacobi法のアルゴリズム
Jacobi法は適当な初期ベクトル $\mathbf{x}^{(0)}$ を仮定し,次の更新規則によってベクトルを更新する.
$$x^{(k)}_{i} = (b_{i} - \sum_{j \neq i} a_{i, j} x^{(k - 1)}_{j}) / a_{i, i};; k = 0, 1, 2, \ldots $$
このアルゴリズムの出処は,
数値解析ノート: 連立1次方程式の定常反復解法(1). Jacobiの反復法 - 休憩室
に詳しく記載したので,よければご参照いただきたい.
Jacobi法の実装
C++でJacobi法を実装すると,コア部分は次のようになるはずである.
for (size_t k = 0; k < ITERS; k++)
{
double y[N] = {0.0};
for (size_t i = 0; i < N; i++)
{
y[i] = x[i];
}
for (size_t i = 0; i < N; i++)
{
x[i] = b[i] + A[i * N + i] * y[i];
for (size_t j = 0; j < N; j++)
{
x[i] -= A[i * N + j] * y[j];
}
x[i] /= A[i * N + i];
}
/* calculate residue */
double Ax[N] = {0.0};
double res = residue_normal_axb(A, x, b, Ax, N);
}
このコードが行っているのは,
ITERS回のベクトルの更新の度に,更新前のベクトルの情報をバッファベクトルyに保存し,それを用いて本来のベクトルの方であるxを要素ごとに更新する
という処理である.そして,更新後には適当に誤差 $\|\mathbf{A}\mathbf{x} - \mathbf{b}\|^{2}$ を測定する(今は固定回数の更新になっているが,この誤差を収束判定に用いることももちろんできる).
パフォーマンス測定,初期ベクトル $\mathbf{x}^{(0)}$ や $(\mathbf{A}, \mathbf{b})$ の用意も含めた完全なコードは次で与えられる.
# include <bits/stdc++.h>
# include "../include/iter.hpp"
using namespace std;
const int N = 64;
const int ITERS = 10 * N * N; /* number of iterations */
int main(int argc, char const *argv[])
{
double A[N * N] = {0.0};
// gen_random_matrix(A, N);
gen_poisson_matrix(A, N);
// out_bin(A, N * N, "./res/A.bin")
double b[N] = {0.0};
gen_random_vector(b, N);
// out_bin(b, N, "./res/b.bin")
/* solve [A] (x) = (b) with given (A, b); where [*] is a matrix, and (*) is a vector */
double x[N] = {0.0};
for (size_t i = 0; i < N; i++)
{
x[i] = 0.1;
}
for (size_t k = 0; k < ITERS; k++)
{
chrono::system_clock::time_point start, end;
double y[N] = {0.0};
for (size_t i = 0; i < N; i++)
{
y[i] = x[i];
}
start = chrono::system_clock::now();
# pragma omp parallel for num_threads(4) /* Jacobi iteration with OpenMP */
for (size_t i = 0; i < N; i++)
{
x[i] = b[i] + A[i * N + i] * y[i];
for (size_t j = 0; j < N; j++)
{
x[i] -= A[i * N + j] * y[j];
}
x[i] /= A[i * N + i];
}
end = chrono::system_clock::now();
double time = static_cast<double>(chrono::duration_cast<chrono::microseconds>(end - start).count() / 1000.0);
/* calculate residue */
double Ax[N] = {0.0};
double res = residue_normal_axb(A, x, b, Ax, N);
/* output */
printf("%e, %lf\n", res, time); /* residue and time (with openmp) */
// output_axb(Ax, b);
}
cout << endl;
for (size_t i = 0; i < N; i++)
{
x[i] = 0.1;
}
for (size_t k = 0; k < ITERS; k++)
{
chrono::system_clock::time_point start, end;
double y[N] = {0.0};
for (size_t i = 0; i < N; i++)
{
y[i] = x[i];
}
start = chrono::system_clock::now();
/* Jacobi iteration without OpenMP */
for (size_t i = 0; i < N; i++)
{
x[i] = b[i] + A[i * N + i] * y[i];
for (size_t j = 0; j < N; j++)
{
x[i] -= A[i * N + j] * y[j];
}
x[i] /= A[i * N + i];
}
end = chrono::system_clock::now();
double time = static_cast<double>(chrono::duration_cast<chrono::microseconds>(end - start).count() / 1000.0);
/* calculate residue */
double Ax[N] = {0.0};
double res = residue_normal_axb(A, x, b, Ax, N);
/* output */
printf("%e, %lf\n", res, time); /* residue and time (without openmp) */
// output_axb(Ax, b);
}
return 0;
}
ヘッダ iter.hpp とその中身 iter.cpp は次の通りである.
# ifndef INCLUDE_GUARD_ITER_HPP
# define INCLUDE_GUARD_ITER_HPP
void gen_random_matrix(double *A, const int N);
void gen_poisson_matrix(double *A, const int N);
void gen_random_vector(double *b, const int N);
double residue_normal_axb(const double *A, const double *x, const double *b, double *Ax, const int N);
void out_axb(const double *Ax, const double *b, const int N);
void out_bin(const double *a, const int n, const std::string fpath);
// void initialize_vector(double *x, const int N);
# endif // INCLUDE_GUARD_ITER_HPP
# include <bits/stdc++.h>
void gen_random_matrix(double *A, const int N)
{
for (size_t i = 0; i < N * N; i++)
{
A[i] = 0.0;
}
// std::random_device seed_gen;
// std::mt19937 engine_mt(seed_gen());
std::mt19937 engine_mt(100);
std::uniform_real_distribution<> dist_ur1(-1.00, 1.00), dist_ur2(1.01, 1.05);
for (size_t i = 0; i < N; i++)
{
for (size_t j = 0; j < N; j++)
{
A[i * N + j] = dist_ur1(engine_mt);
}
A[i * N + i] += (double)N * dist_ur2(engine_mt);
}
}
void gen_poisson_matrix(double *A, const int N)
{
for (size_t i = 0; i < N * N; i++)
{
A[i] = 0.0;
}
for (size_t i = 0; i < N; i++)
{
A[i * N + i] = 2.0;
if (i >= 1)
{
A[i * N + i - 1] = -1.0;
}
if (i <= N - 2)
{
A[i * N + i + 1] = -1.0;
}
}
}
void gen_random_vector(double *b, const int N)
{
for (size_t i = 0; i < N; i++)
{
b[i] = 0.0;
}
// std::random_device seed_gen;
// std::mt19937 engine_mt(seed_gen());
std::mt19937 engine_mt(100);
std::uniform_real_distribution<> dist_ur(-1.00, 1.00);
for (size_t i = 0; i < N; i++)
{
b[i] = (double)N * dist_ur(engine_mt);
}
}
double residue_normal_axb(const double *A, const double *x, const double *b, double *Ax, const int N)
{
double r = 0.0;
for (size_t i = 0; i < N; i++)
{
for (size_t j = 0; j < N; j++)
{
Ax[i] += A[i * N + j] * x[j];
}
r += (b[i] - Ax[i]) * (b[i] - Ax[i]);
}
double r0 = 0.0;
for (size_t i = 0; i < N; i++)
{
r0 += b[i] * b[i];
}
r = sqrt(r / r0);
return r;
}
void out_axb(const double *Ax, const double *b, const int N)
{
printf(" Ax = {");
for (size_t i = 0; i < N - 1; i++)
{
printf("%.2f, ", i, Ax[i]);
}
printf("%.2f}\n", N - 1, Ax[N - 1]);
printf(" b = {");
for (size_t i = 0; i < N - 1; i++)
{
printf("%.2f, ", i, b[i]);
}
printf("%.2f}\n", N - 1, b[N - 1]);
printf("\n");
}
void out_bin(const double *a, const int n, const std::string fpath)
{
std::ofstream fout;
fout.open(fpath, std::ios::out | std::ios::binary | std::ios::trunc);
for (size_t i = 0; i < n; i++)
{
fout.write((char *)&a[i], sizeof(double));
}
fout.close();
}
Jacobi法の実験結果
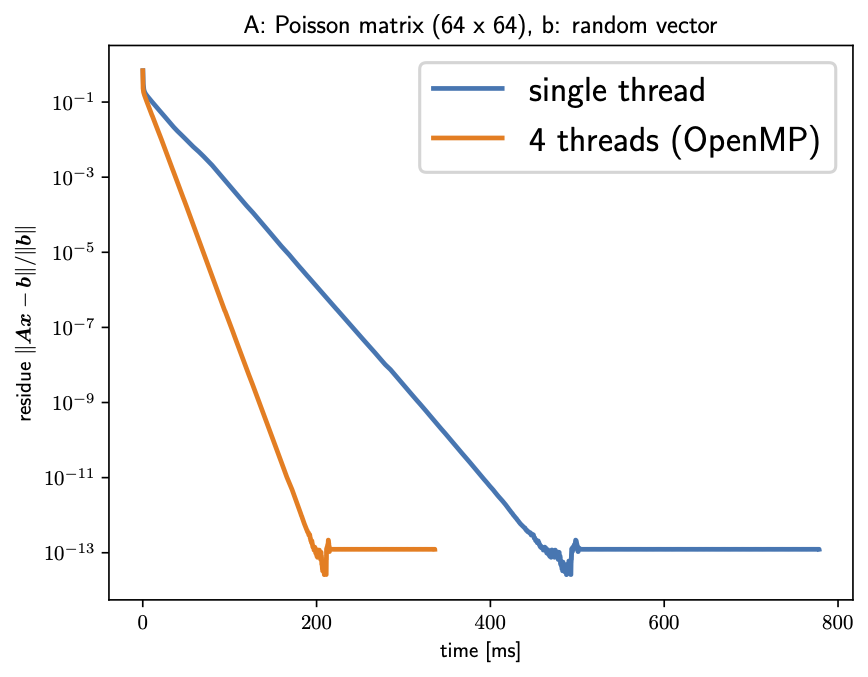
以上のプログラムを実行すると,ベクトル $\mathbf{x}_{k}$ を更新する度に変化する誤差 $\|\mathbf{A}\mathbf{x}_{k} - \mathbf{b}\|^{2}$ の挙動は次のようになる.
確かに,反復回数に応じて誤差が減少し,収束しているのが分かる.なお,この収束挙動は $ (\mathbf{A}, \mathbf{b}) $ の性質に大きく依存することに注意されたい.
最後に
以上,ごくごく簡単なアルゴリズムではあるが,連立一次方程式の定常反復法の最も簡単な場合であるJacobi法の紹介をした.一連のソースコードはGithubリポジトリとして公開しておいたので,興味があれば手元のPCにcloneして遊んでみてほしい:
https://github.com/tarotene/iterative-methods
この記事が,読者の皆さんの反復法への,ひいては数値解析への入門の一助となれば幸いである.
(2020/03/17追記)
Jacobi法をそのままちょっとだけ改良したGauss-Seidel法については以下の記事を参照.
https://qiita.com/tarotene/items/8b6bfbe5d60ccb182ffd
参考文献
- R.Barrett, et al. 『反復法Templates』この記事を書こうと思った最初のきっかけ.アルゴリズムの導出のみならず,数学的にしっかりとした解析もついていて読みやすい.絶版になってしまったのが悔やまれる.
- 齊藤宣一 『数値解析入門』 日本語で書かれた画期的な数値解析の教科書.連立一次方程式の反復解法のみならず,例えば常備分方程式の初期値問題などについても示唆に富む記述が多く,研究にも役に立つ.個人的には,この本に積分変換の数値的な取扱いに関するちょっと詳しめの解説が付けば究極完全体だと思う.